4.5.9. Особые случаи пресечения поверхностей второго порядка. Как строится линия пересечения поверхностей вращения в особых случаях?

Известно, что линией пересечения двух поверхностей второго порядка является кривая четвертого порядка¹.

Но в случаях, соответствующих приведенным ниже теоремам, эта линия будет кривой второго порядка, т.е. плоской кривой. Рассматривая особые случаи пересечения поверхностей второго порядка (три теоремы), необходимо отметить, что линия их пересечения может быть найдена без использования вспомогательных секущих поверхностей. В этих случаях одна проекция линии пресечения находится по теореме, а вторая – с использованием условия принадлежности

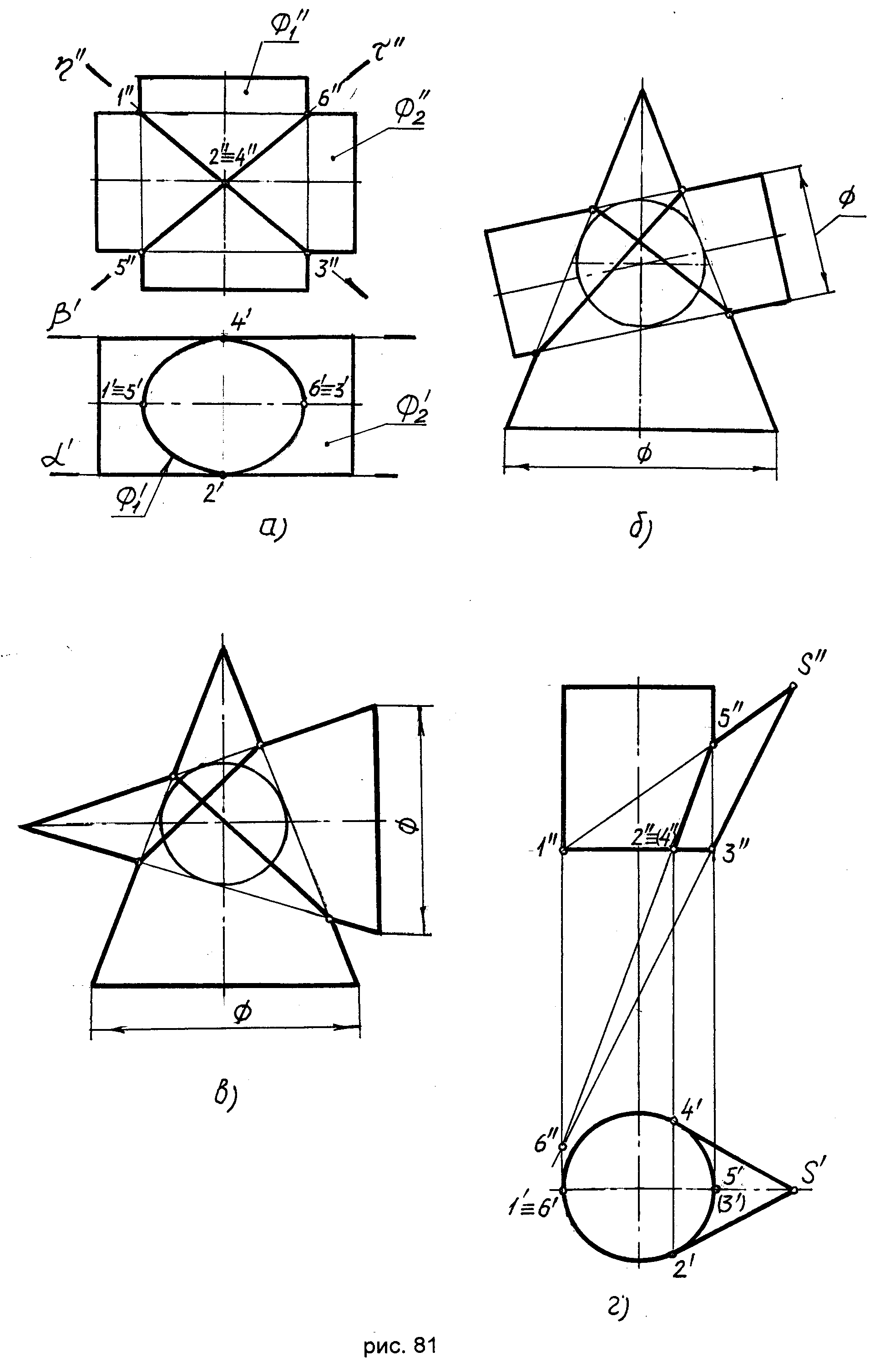
1. Теорема о двойном прикосновении:если две поверхности второго порядка имеют две точки касания, то линия их пересечения распадается на две кривые второго порядка.

Точками касания поверхностей называются точки, через которые проходят плоскости, касательные одновременно к той и другой поверхностям.

На рис. 81а показано пересечение двух цилиндрических поверхностей второго порядка Ф₁и Ф₂. Поверхности Ф₁и Ф₂имеют две общие касательные плоскости(),() и две общие точки касания 2 и 4. Поэтому по теореме 1 они пересекаются по двум плоским кривым второго порядка, расположенным в плоскостяхи. Плоскостиипроходят через прямую 2 - 4₂, откуда следует, что плоскостиифронтально-проецирующие. Следовательно, принадлежащие им кривые пресечения проецируются на плоскость₂в отрезки прямых, проходящие через опорные точки 1, 3, 5, 6. Горизонтальные проекции линий пересечения будут совпадать с горизонтальной проекцией Ф₁эллиптической цилиндрической поверхности Ф.

2. Теорема Монжа:если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка (или вписаны в нее), то они пересекаются по двум кривым второго порядка.

Эта теорема является частым случаем теоремы 1. Практическое использование теоремы возможно в случае, когда две поверхности описаны около сферы или вписаны в нее.

На рис. 81б и в приведены примеры построения линии пересечения поверхностей вращения для таких случаев.

3. Теорема: если две поверхности второго порядка пересекаются по одной кривой второго порядка, то они пересекаются по второй кривой второго порядка.

На рис. 81г цилиндрическая и коническая поверхности имеют в основании общую окружность 1-2-3-4-1, т.е. линию пересечения – кривую второго порядка. На основании теоремы 3 находим вторую линию пересечения - кривую второго порядка 5-2-6-4-5. Опорные точки 1, 3, 5, 6 получены в пересечении очерковых образующих. Точки 2 и 4 – точки касания поверхностей. Эта теорема также является частным случаем теоремы 1.

4.6. Пересечение прямой с поверхностью (общий случай)

4.6.1. Каков алгоритм решения задачи для определения точек пересечения линии с поверхностью ?

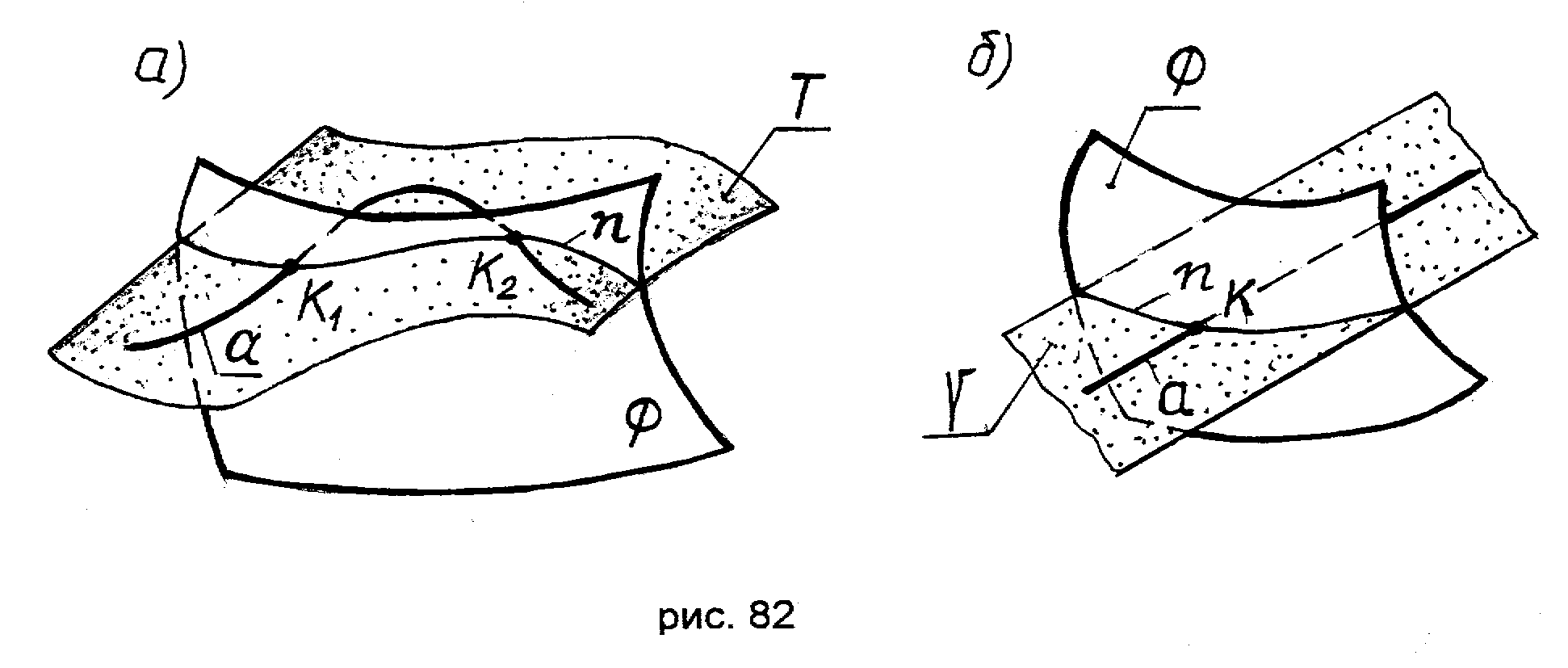
В общем случае для определения точек пересечения линии aс поверхностью(рис. 82а) необходимо выполнить следующее:

1. заключить данную линию aво вспомогательную поверхность    a;

2. определить линию пересечения nвспомогательной поверхностис заданной поверхностью  n =   ;

3. отметить точки пересечения K₁,K₂… полученной линииnс заданнойa  K₁,K₂… = n a;

Для определения точек пересечения прямой с поверхностью (рис 82б) в качестве вспомогательной поверхности следует брать плоскость.

Проследим как решается эта задача на комплексном чертеже.

ПРИМЕР 1. Построить точки пересечения прямой aс произвольной цилиндрической поверхностью(рис 83а).

РЕШЕНИЕ.

Анализируя заданные пересекающиеся фигуры, отмечаем, что прямая aи поверхностьзанимают общее (непроецирующее) положение. Следовательно решаем 1ГПЗ, общий случай. Отсюда:

1. заключаем прямую aво вспомогательную фронтально-проецирующую плоскость()    a(рис 83б);

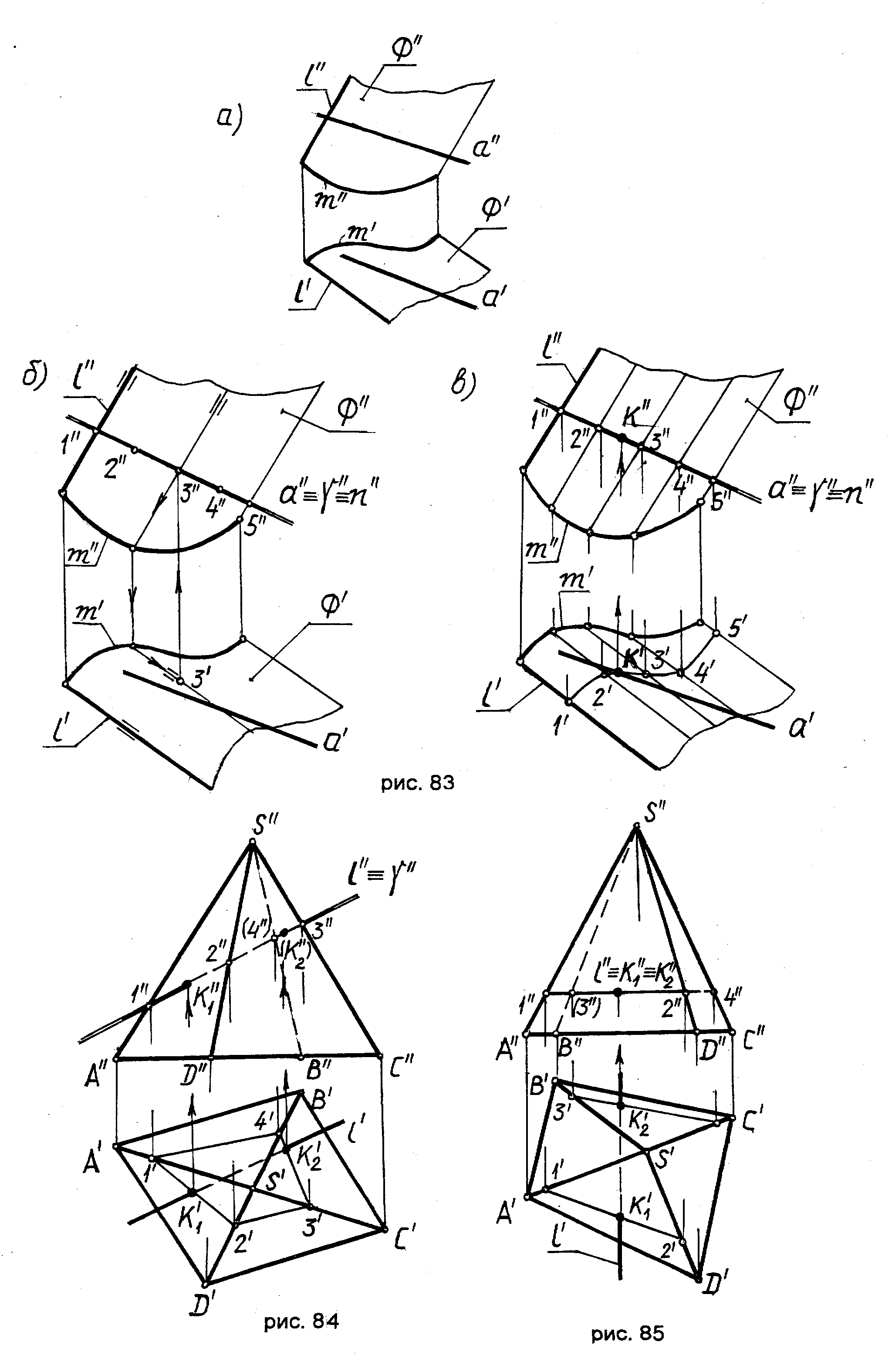
2. определяем кривую nпересечения плоскостис поверхностью(2 ГПЗ, частный случай 2). В этом случае фронтальная проекция n"линии пересеченияnсовпадает с основной проекциейплоскости  n  ;

Для построения горизонтальной проекции nкривойnотмечаем наa    nпроизвольные точки 1, 2, 3, 4, 5и находим горизонтальные проекции по условию принадлежности их поверхностис помощью образующих (см. построение горизонтальной проекции3точки 3 на рис 83б).

Соединив точки 1, 2, 3, 4, 5 плавной кривой, получим горизонтальную проекциюnкривой пересеченияn (рис 83в);

3. отмечаем точку K пересечения прямой a с кривой пересечения n  K = a  n. С помощью линии связи находим K. K(K, K) – искомая точка пересечения прямой a с заданной поверхностью .

ПРИМЕР 2. Построить точки пересечения прямой l с пирамидой SABCD (рис 84).

РЕШЕНИЕ.

Анализируя заданные пересекающиеся геометрические фигуры, отмечаем, что прямая lи грани пирамиды занимают общее (непроецирующее) положение. Следовательно, решаем 1 ГПЗ, общий случай. Отсюда:

1. заключаем прямую lво вспомогательную фронтально–проецирующую плоскость()    l ;

2. строим сечение пирамиды SABCDплоскостью(2 ГПЗ, частный случай 2). При этом фронтальная проекция четырёхугольника сечения совпадает с основной проекциейплоскости. Отмечаем фронтальные проекции точек пересечения рёбер пирамиды с основной проекцией плоскости.

1 = SA ; 2 = SB  ; 3 = SC  ; 4 = SD  ;

Горизонтальные проекции 1, 2, 3, 4находим по принадлежности их соответствующим рёбрам пирамиды. Четырёхугольник 1234– горизонтальная проекция сечения;

3. отмечаем точки K₁иK₂пересечения прямойaсо сторонами фигуры сечения. ПоK₁иK₂определяемK₁иK₂.

K₁(K₁, K₁) иK₂(K₂, K₂) – точки входа и выхода прямойl.

ПРИМЕР 3. Иллюстрирует решение задачи на определение точек пересечения фронтально проецирующей прямойlс поверхностью пирамидыSABCD (1 ГП3, частный случай 2). При этом фронтальные проекцииK₁иK₂точек пересеченияK₁иK₂совпадают с основной проекциейlпрямойl.

Горизонтальные проекции K₁иK₂построены по условию принадлежности их соответственно гранямSADиSBCс помощью прямых 12 и 34.

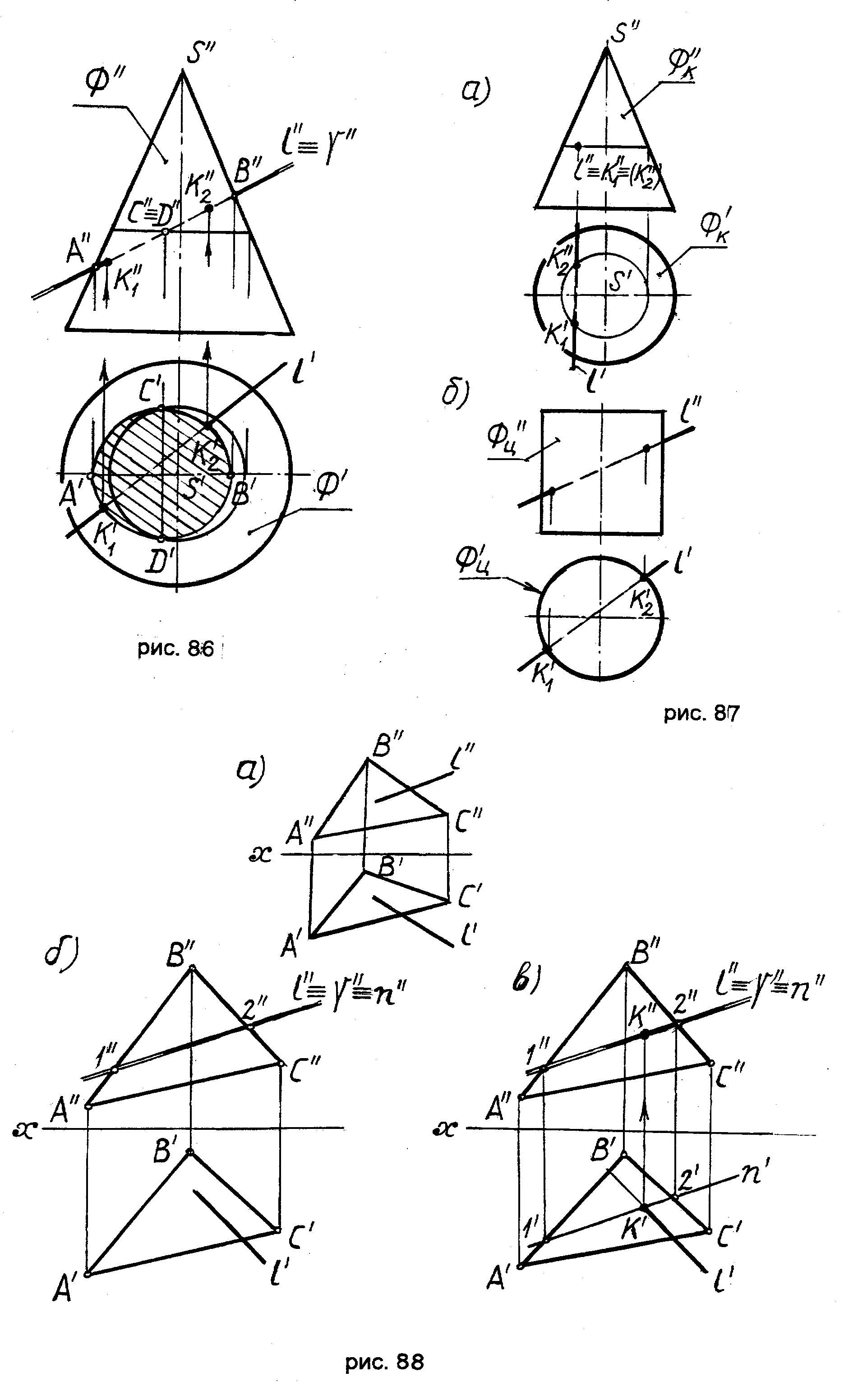
ПРИМЕР 3. Построить точки пересечения прямой lс поверхностью конуса (рис 86).

РЕШЕНИЕ.

Анализируя исходные данные, отмечаем, что прямая lи коническая поверхностьзанимают общее (непроецирующее) положение. Следовательно, решаем 1 ГПЗ, общий случай. Отсюда:

1. заключаем прямуюlво вспомогательную фронтально-проецирующую плоскость()    l ;

2. Строим сечение конической поверхностиплоскостью(1 ГПЗ, частный случай 2). В сечении конической поверхности плоскостью, не параллельной ни одной из его образующих, получим эллипс (см п.4.3.3). При этом фронтальная поверхность эллипса известна:она совпадает с основной проекциейплоскостии проецируется в отрезок прямой AB  , равный по величине большой оси эллипса. Малая ось эллипсаCD спроецируется на плоскость ₂ в точку C  D, расположенную в середине отрезка AB.

Горизонтальные проекции точек A, B, C, D строим по условию принадлежности их конической поверхности. Зная большую и малую оси эллипса, известным способом строим эллипс;

3. отмечаем точки K₁иK₂пересечения прямойl с эллипсом. ПоK₁иK₂определяем точкиK₁иK₂.

K₁(K₁, K₁) иK₂(K₂, K₂) – точки входа и выхода прямойl.

ПРИМЕР 4 (рис 87). Иллюстрирует решения задач на пересечение линий и поверхности:

а) прямая l- фронтально-проецирующая, а поверхностьпрямого кругового конуса – общего положения (1 ГПЗ, частный случай 2) (рис 87а);

б) прямая l– общего положения, а поверхностьпрямого кругового цилиндра – проецирующая (1 ГП3, частный случай 2) (рис 87б).

Решения задач ясны из чертежа и не требуют каких-либо пояснений.

ПРИМЕР 5. Построить точку пересечения прямой lс плоскостью(ABC) (рис 88а).

РЕШЕНИЕ.

Анализируя исходные данные, отмечаем, что прямая lи плоскость(ABC) занимают общее положение. Следовательно, решаем 1ГПЗ, общий случай. Отсюда:

1. заключаем прямуюlво вспомогательную фронтально-проецирующую плоскость()    l ;

2. определяем прямуюnпересечения плоскостис плоскостью(ABC) (2 ГП3, частный случай 2). При этом фронтальная проекция nлинии n совпадает с основной проекциейплоскостиn   и как прямая, лежащая в плоскости(ABC), определяется точками 1'' и 2''(рис 88б). Горизонтальную проекциюnпрямойnнаходим, как недостающую проекцию прямой, лежащей в плоскости(ABC) и определяемой точками 1и 2(рис 88в).

3. отмечаем точку Kпересечения прямойn (1, 2) с прямой l   K = n l . ПоKнаходим.K(K, K) – искомая точка.