
Blatov_lek
.pdf
Скалярное произведение векторов, заданных своими проекциями
Пусть два вектора заданы своими разложениями по ортам в декартовой системе координат
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a xa |
i |
ya |
j |
za |
k; |
b |
xb |
i |
yb |
j |
zb |
k |
|
|
Тогда скалярное произведение
a b xa i ya j zak xb i yb j zbkxaxb i i xayb i j za zb k k
Помня, что от перестановки сомножителей скалярного произведения результат не меняется, получим
|
|
|
|
|
|
|
|
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
i |
|
i |
j |
j |
k |
k |
i |
j |
i |
k |
j |
k |
|||||||||||
Учитывая эти результаты, найдем
a b xaxb yayb zazb
Скалярное произведение векторов, заданных проекциями в декартовой системе координат, равно сумме произведений одноименных координат.
Замечание Формула справедлива только в ортонормированном базисе.
Косинус угла между векторами определится выражением
|
a |
|
|
|
|
|
|
xaxb yayb zazb |
|
|
|
|||||||
cos |
b |
|
|
|
|
|
|
|
||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b |
2 |
2 |
2 |
|
2 |
2 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
xa |
ya |
za |
|
xb |
yb |
zb . |
||
|
|
|
|
|
|
|
|
|||||||||||
Контрольные вопросы
1.Дать определение скалярного произведения двух векторов.
2.Какие значения могут получиться в результате скалярного произведения?
3.Перечислите свойства скалярного произведения.
4.Чему равно скалярное произведение вектора самого на
себя?
81

5.Как вычислить скалярное произведение, если векторы заданы своими координатами в ортонормированном базисе?
6.Сформулируйте необходимое и достаточное условие перпендикулярности двух векторов.
7.Как найти угол между векторами?
Задачи для самостоятельного изучения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. Зная, что |
|||||||||||||||
1. |
|
|
Векторы a и b образуют угол |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
a |
|
3, |
b |
|
4 , вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
1) ab ; 2) a |
2 ; 3) b 2 ; 4) |
a b ; 5) 3a 2b |
a 2b ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
6) a |
|
|
2 ; 7) 3a 2b |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Даны векторы a 4; 2; 4 , |
|
|
|
|
|
6; 3;2 . |
||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 ; |
|
|
|
|
|
|
|
|
|
2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1)ab; 2) |
3) |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
4) 2a 3b |
a 2b |
; |
|
|
5) a |
|
|
2 |
|
6) a |
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3. |
|
|
Даны единичные |
|
|
|
векторы |
|
|
|
|
|
a, b, c , |
удовлетворяющие |
||||||||||||||||||||||||||||||||||||||||||||||||
условию a |
|
c 0 . Вычислить |
a |
|
|
|
|
|
c ca . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
4. |
|
|
Даны |
векторы |
a, b, c , |
удовлетворяющие условию |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
c 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
3, |
|
|
|
1, |
c |
4 , определить |
||||||||||||||||||||||||||||||||||||||||||
|
Зная, |
|
|
|
|
что |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
|
c ca . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
5. |
|
|
Известно, что |
|
a |
3, |
|
b |
5 . Определить, при каком |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
будут взаимно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
значении k векторы a kb, |
a kb |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
перпендикулярны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 1; 2;4 , |
||||||||||||||||||||||||
6. |
|
|
Даны |
|
вершины |
|
треугольника |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
B 4; 2;0 |
и C 3; 2;1 . |
Определить его внутренний угол |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
при вершине B и внешний угол при вершине A . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7. |
|
|
Вычислить проекцию вектора a 5;2;5 на ось вектора |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b 2; 1;2 .
82

8.Найти проекцию вектора d 4; 3;2 на ось, составляющую с координатными осями равные острые углы.
9.Даны векторы a 1; 3;4 , b 3; 4;2 и
c 1;1;4 . Вычислить prb c a . |
вектору 6, 8, 7,5 , |
10. Вектор x , коллинеарный |
образует острый угол с осью OZ. Зная, что длина вектора равна 50, найти его координаты.
Ответы к задачам для самостоятельного изучения
1.1) -6; 2) 9; 3) 16; 4) 13; 5) -61; 6) 37; 7) 73.
2.1) 22; 2)6; 3) 7; 4)-200; 5) 129; 6) 41.
3.-3/2.
4.-13.
5.53 .
6. Внутренний при вершине B 450 , внешний при
A2700 .
7.6.
8.
 3
3
9.5.
10.{-24,32,30}.
Векторное произведение векторов
Введем нелинейную операцию над векторами. Эта операция существует только в трехмерном векторном пространстве, на плоскости она не определена.
83
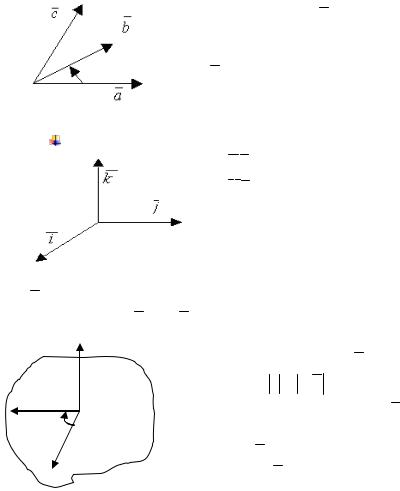
Определение Упорядоченная
тройка векторов a, b, c называется
правой, если наблюдателю, находящемуся на конце вектора, кратчайший поворот от
a к b кажется происходящим против часовой стрелки.
В противном случае тройка векторов левая.
Пример
ijk правая тройка jik левая тройка
|
Замечание |
|
|
Тройки |
компланарных |
векторов |
не |
||
относятся ни к правым, ни к левым |
||||
|
Определение |
Векторное |
||
произведение вектора |
a на вектор |
|||
b
-вектор c a b a, b , определяемый следующим образом:
1)длина его равна площади параллелограмма,
c b
построенного на векторах a и b , т.е.
с a
 b sin ,
b sin ,
где - угол между векторами a и b ;
|
|
2) |
вектор |
c |
перпендикулярен |
a |
векторам a и b ; |
|
|
||
|
|
|
|||
|
3) |
векторы a, b, c |
после приведения к |
||
общему началу образуют правую тройку векторов.
Свойства векторного произведения
1.a b = -b a ;
2.a + b c = a c + b c ;
3.α a b = α a b ; a - вещественное число;
84

4. |
|
a b |
|
равен |
площади |
параллелограмма, |
|
|
|||||
|
|
|
|
|
|
|
построенного на векторах a , b ;
5.если a 0,b 0 , и a b = 0 , то a || b .
Векторное произведение – момент M = r F или вектор b |
- |
||
сила, приложенная к какой-либо точке |
M , а вектор a |
идет из |
|
точки O в мочку M , то вектор |
с - момент |
силы |
b |
относительно точки O . |
|
|
|
Векторное произведение векторов, заданных своими проекциями в декартовой системе координат
Пусть два вектора заданы своими разложениями по ортам в декартовой системе координат
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a xa |
i |
ya |
j |
za |
k; |
b |
xb |
i |
yb |
j |
zb |
k; |
||
Найдем векторное произведение
a b xa i ya j zak xb i yb j zbkxaxb i i xa yb i j za zb k k
Помня, что от перестановки сомножителей векторного произведения результат меняет знак, получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i |
|
i |
|
j |
j |
k |
|
k |
|
|
i |
|
|
j |
j |
i |
|
k, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
j |
|
k |
k |
j |
i, |
k |
i |
i |
k |
j. |
||||||||||||||||||||||||||||||
Учитывая эти результаты, найдем
a b yazb zayb i xazb zaxb j xayb yaxb k
или
i j k
a b xa ya za xb yb zb
Т.о., вектор, получаемый в результате векторного произведения векторов, заданных своими координатами, получается из определителя, первой строкой которого являются координатные орты, вторая и третья строки состоят, соответственно, из координат первого и второго сомножителей.
85
Контрольные вопросы по теме «Векторное произведение»
1.Какая тройка векторов считается правой (левой)?
2.Что такое векторное произведение двух векторов?
3.Каков геометрический смысл модуля результата векторного произведения?
4.Как перемножить векторно векторы, заданные своими координатами в декартовой системе координат?
5.В чем состоит условие коллинеарности векторов?
6.Какой вид условие коллинеарности имеет в ортонормированной системе координат
Задачи для самостоятельного изучения |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Определить, какой является |
|
|
тройка векторов a, b, c |
||||||||||||||||||||||||||
|
(правой или левой), если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол |
|
|
|
|
|
|
||||||||||
2. |
Векторы a и |
b образуют |
. Зная, что |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 , вычислить |
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
a |
6, |
b |
|
|
b |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
10, |
|
|
|
2 и a |
|
12 . Вычислить |
|
a, |
|
|
. |
||||||||||||||||
3. |
Даны:, |
a |
|
|
b |
b |
|
b |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Векторы a и b взаимно перпендикулярны. Зная, что
|
3, |
|
4 |
a |
b |
||
|
|
|
|
86
Вычислить:
а) a b a b ; a b б) 3a b a 2b .
5.Векторы a и b образуют угол 23 .
|
|
1, |
|
2 , вычислить: |
Зная, что |
a |
b |
||
|
|
|
|
|
а) a |
|
2 ; б) |
|
2a |
|
a 2b |
|
2 ; в) |
|
a 3b |
3a |
|
|
2 . |
|||||||||||||
b |
|
b |
|
b |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
a 3, 1,2 ; |
|
|
1,2, 1 . Найти |
||||||||||||||||
6. Даны |
|
|
|
векторы |
b |
||||||||||||||||||||||
|
координаты |
|
|
|
векторных |
|
|
|
|
|
произведений: |
||||||||||||||||
|
|
|
; б) 2a |
|
|
|
|
; в) 2a |
|
2a |
|
. |
|||||||||||||||
|
а) ab |
b |
b |
b |
b |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
7.Даны точки A 1,2,0 , B 3,0, 3 и C 5,2,6 . Вычислить площадь треугольника ABC .
8.Даны вершины треугольника A 1, 1,2 , B 5,2,6 и
C 1,3, 1 . Вычислить длину его высоты, опущенной из
вершины B на сторону AC .
9. Вектор x , перпендикулярный к векторам a 4, 2,3 и b 0,1,3 , образует с осью Oy тупой угол. Зная, что длина x равна 26, найти его координаты.
Ответы к задачам для самостоятельного изучения
1.а) правая; б) левая; в) левая; г) правая; д) векторы компланарны; е) левая.
2.15.
3.16.
4.а) 24, б) 60.
5.а) 3; б) 27; в) 300.
6.а) {5,1,7}; б) {10,2,4}; в) {20,4,28}.
7.14 .
8.5 .
9.{-6,-24,8}.
87
Смешанное произведение векторов
Определение Смешанное произведение трех векторов
a, b, c - число
a, b , c a b c .
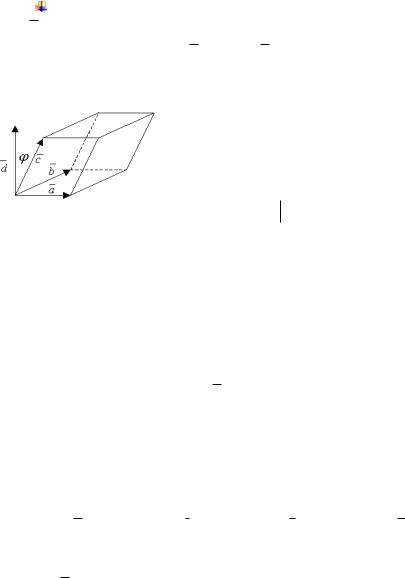
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
|
a, b, c |
|
|
правая |
|
тройка |
|||||||||||
|
векторов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Действительно, |
|
|
|
|
|
объем |
|||||||||||||
|
параллелепипеда, |
|
|
построенного на |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторах a, b, c , |
|
|
равен |
площади |
|||||||||||||||
|
|
|
|
|
a, |
|
|
|
|
|
|
|
|
|
|
cos . |
||||
|
основания |
|
b |
|
на |
высоту |
|
c |
|
|||||||||||
Здесь |
|
|
|
|
|
и |
|
. |
|
|
|
|
||||||||
- угол между векторами |
d |
= |
|
|
|
|
|
c |
|
|
|
|
||||||||
a, b |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Замечание Знак смешанного произведения совпадает со |
||||||||||||||||||||
знаком |
cos , и поэтому |
смешанное |
произведение |
|||||||||||||||||
положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая.
Если перемножаемые векторы лежат в одной плоскости
( cos 0 ),
то
a, b , c 0
- необходимое и достаточное условие компланарности векторов.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a xa |
i |
ya |
j |
za |
k; |
b |
xb |
i |
yb |
j |
zb |
k; |
c xc |
i |
yc |
j |
zc |
k |
|
||
Известно, что
a b yazb zayb i xazb zaxb j xayb yaxb k
Скалярно умножим этот вектор на вектор c и, учитывая свойства скалярного произведения, получим
a b c yazb zayb xc xazb zaxb yc xayb yaxb zc
88

Это выражение может быть получено при вычислении
определителя |
|
|
|||
|
|
|
xa |
ya |
za |
|
|
|
|||
a |
|
c |
xb |
|
|
b |
yb |
zb |
|||
|
|
|
xc |
yc |
zc |
по элементам третьей строки, исходя из правила вычисления определителя.
a b c a b c c a b
Поэтому смешанное произведение трех векторов обозначают как a, b, c , не подчеркивая при этом, какая пара векторов умножается векторно.
Свойства смешанного произведения
1.a b c b c a c a b
2.При перестановке двух сомножителей смешанное
произведение меняет знак 3. Смешанное произведение обращается в нуль, если
хотя бы один из перемножаемых векторов 0 два из векторов коллинеарны три – компланарны.
4. |
|
ax |
ay |
az |
Вычисление |
смешанного |
|
abс |
bx |
by |
bz |
произведения |
|
|
|
|
||||
|
|
cx |
cy |
cz |
|
|
.
5.Объем пирамиды равен v 16 abс одна шестая объема
параллелепипеда, построенного на ее сходящихся в одной вершине ребрах.
6. Вектора компланарны, если их смешанное произведение равно нулю.
89
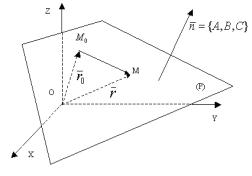
Лекция 7 Плоскость в пространстве R3
Изучение геометрических объектов с помощью метода координат начнем с простейших поверхностей и линий, а именно: плоскостей и прямых. Поверхности первого порядка – плоскости. В зависимости от выбора параметров, определяющих положение плоскости, получаем несколько видов уравнений плоскости.
Теорема Всякая плоскость в пространстве определяется линейным уравнением
Ax By Cz D 0
|
|
Уравнение |
|
называют |
|
общим |
|
уравнением плоскости |
|||
Действительно, |
|
||
пусть в пространстве |
|||
R3 задана |
плоскость |
||
P . |
|
|
|
Выбираем |
на |
P |
|
какую-либо |
|
точку |
|
M0 (x0 , y0 , z0 ) , и в некоторой точке плоскости |
P построим |
||
ненулевой вектор n A, B,C , перпендикулярный плоскости |
|||
P . |
|
|
|
Для того, чтобы произвольная точка |
M (x, y, z) |
||
пространства принадлежала плоскости P , необходимо |
и |
||
достаточно, чтобы M0M n , т.е |
|
|
|
n r - r0 0 |
|
|
|
- уравнение называется векторным уравнением плоскости.
Т.к. n A, B,C и r - r0 x x0 , y y0 , z z0 ,
то скалярное произведение можем заменить через координаты сомножителей, а именно:
90
