
Blatov_lek
.pdf
Лекция 12 Преобразования системы координат на плоскости
Параллельный перенос системы координат
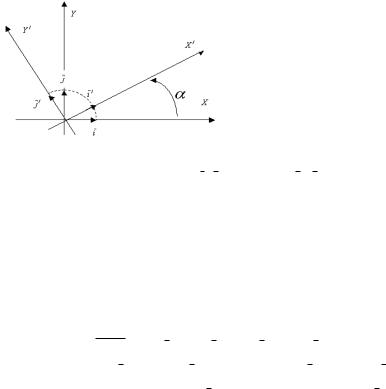
Мы рассматриваем прямоугольную декартову систему координат. При параллельном переносе системы координат сохраняется направление координатных осей, но меняется положение начала координат.
начало O Тогда
Пусть Oxy - "старая" система координат, а O x y - "новая" система координат. Пусть произвольная точка M имеет координаты ( x, y )
в "старой" системе, и она же имеет координаты ( x , y )в новой системе,
кроме того, пусть новое имеет координаты ( a,b ) в "старой" системе.
. OM OO O M
Т.к. при параллельном переносе осей координат базис не меняется, то при сложении векторов можно складывать их координаты.
Следовательно, имеем
x x a y y b
Формулы есть формулы перехода, связывающие "старые" и "новые" координаты.
151
Поворот осей координат
Сейчас мы рассматриваем преобразование, заключающееся в повороте координатных осей с сохранением начала координат .
Пусть точка M имеет координаты ( x, y ) в
"старой" системе и координаты ( x , y )в
"новой" системе, – угол поворота осей координат, отсчитываемый в положительном направлении от "старой"
оси Ox . В данном случае
происходит изменение базиса (i , j) на базис (i , j ) .
|
|
|
и |
|
|
|
|
|
|
|
|||
Запишем координаты векторов i |
|
j в базисе (i |
, j) |
||||||||||
|
|
|
|
|
|
|
cos , sin |
||||||
|
|
|
|
||||||||||
|
i cos , cos |
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos , sin |
|
|
|||||
j cos |
2 |
|
|||
|
|
|
|
|
|
Тогда:
OM x i y j x i y j
x cos i sin j y sin i cos jx cos y sin i x sin y cos j,
т.е., мы получили
x x cos y sin y x sin y cos
или, в матричной форме
x |
cos |
|
|
|
|
|
|
|
y |
sin |
|
Формулы выражают "старые"
sin |
|
|
|
|
x |
||||
|
|
|
|
|
cos |
|
|
|
|
|
y |
|||
координаты через "новые".
152
Обозначим матрицу
тогда
cos |
sin |
A , |
|||
|
|
|
|
|
|
|
|
cos |
|
|
|
sin |
|
|
|
||
x |
|
|
|
|
|
x |
|
||||
|
|
A |
|
|
|
|
|
|
|
|
|
y |
y |
|
|||
Как найти выражение "новых" координат через "старые"? Поскольку матрица А невырожденная, то существует
обратная матрица A-1.
Умножим соотношение (45) слева на A-1 и получим
x |
|
|
|
|
|
|
|
|
x |
x |
|||||||
A 1 |
|
A 1 A |
|
|
A 1A |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
y |
y |
|||||
поскольку A-1*A, т.е. единичная матрица, то
|
|
|
|
x |
|
x |
|
||||
|
|
|
A 1 |
|
|
|
|
|
|
|
|
y |
|
y |
|||
cos |
sin |
||||
где, очевидно A 1 |
|
|
|
|
|
|
sin |
|
|
||
|
cos |
||||
Классификация кривых второго порядка
Преобразованиями, которые переводят декартову прямоугольную систему координат xOy в другую декартову
прямоугольную систему координат x Oy , являются поворот осей и перенос начала координат.
Теорема Если в некоторой декартовой прямоугольной системе координат линия задается алгебраическим уравнением степени n, то в любой другой декартовой прямоугольной системе координат уравнение линии будет иметь такой же вид и порядок.
Покажем, что при помощи поворота всегда можно избавиться от члена, содержащего смешанное произведение координат Bxy .
153
После поворота осей на угол старые координаты связаны с новыми формулами
Ax2 Cy2 Dx Ey F Ax 2 2Ax x0 Ax02 Cy 2 2Cy y0 Cy02
Dx Dx0 Ey Ey0 F 0.
xx cos y sin .
y x sin y cos
Перепишем уравнение в новых координатах:
Ax2 Bxy Cy2 Dx Ey F Ax 2 cos2 2Ax y sin cos Ay 2 sin2Bx 2 sin cos Bx y sin2 Bx y cos2 By 2 sin cos
Cx 2 sin2 2Cx y sin cos Cy 2 cos2
Приравняем нулю получившийся коэффициент перед x y :
2Asin cos Bsin2 B cos2 2C sin cos 0 .
Или
C A sin 2 B cos 2 0 .
Если |
A C , так как B 0 , то cos 2 0 |
, то есть |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
Если |
|
же |
A C , поделив на cos 2 , |
мы получим, что |
|||||||
tg2 |
B |
|
|
B |
, то есть |
1 |
arctg |
B |
. |
|
|
|
|
C A |
A C |
2 |
|
A C |
|
||||
Итак, в новой повернутой системе координат уравнение примет вид
A x 2 C y 2 D x E y F 0 .
Теперь B = 0.
Покажем, что переносом начала координат можно избавиться от членов первого порядка Dx и Ey в уравнении, которое будет иметь вид
Ax2 Cy2 Dx Ey F 0 .
Если система координат xOy получается из системы координат x Oy переносом на вектор ( x0 , y0 ), то связь координат в этих системах задается следующими равенствами:
154
x x x0 y y y0
Перепишем уравнение в новых координатах:
Обозначим через F′ свободный член:
F Ax02 Cy02 Dx0 Ey0 F .
Приравняем нулю коэффициенты при x′ и y′:
2Ax0 D 0
2Cy0 E 0
Если A 0 , то D 0 , если C 0 , то E 0 , и уравнение не содержит членов первого порядка. Поэтому предположим, что A 0 и C 0 . Тогда для координат вектора ( x0 , y0 ) мы
получим следующие выражения: x |
D |
, |
y |
E |
. |
|
|
||||
0 |
2A |
|
0 |
2C |
|
|
|
|
|||
В новых координатах уравнение примет вид
Ax 2 Cy 2 F 0 .
Мы показали, что всегда найдется такая система координат, в которой уравнение линии второго порядка будет иметь вид
A x 2 B y 2 1 , если F 0 ,
или
A x 2 B y 2 0 , если F 0 .
Теорема Существует система координат, в которой уравнение линии второго порядка принимает один из следующих девяти канонических видов:
1. |
|
x2 |
|
|
|
|
y2 |
|
1 – уравнение эллипса; |
a2 |
|
b2 |
|||||||
|
|
|
|
|
|
|
|||
2. |
|
x2 |
|
|
y 2 |
|
1 – уравнение мнимого эллипса; |
||
a 2 |
|
b2 |
|
||||||
|
|
|
|
|
|
|
|
||
3. |
|
x2 |
|
|
y 2 |
|
1 – уравнение гиперболы; |
||
|
a 2 |
|
|
|
|||||
|
|
|
|
|
|
b2 |
|
|
|
4. |
|
y2 2 px – уравнение параболы; |
|||||||
155
5. |
|
x2 |
|
|
|
y2 |
|
|
0 – уравнение пары пересекающихся прямых; |
|
a2 |
|
b2 |
|
|||||||
|
|
|
|
|
|
|
|
|||
6. |
|
x2 |
|
|
y2 |
|
|
0 |
– уравнение пары мнимых пересекающихся |
|
|
a2 |
b2 |
|
|
||||||
|
|
|
|
|
|
|
|
|||
прямых; |
|
|
|
|
|
|
|
|||
7. y2 |
b2 |
0 – уравнение пары параллельных прямых; |
||||||||
8. y2 |
b2 |
0 |
– уравнение пары мнимых параллельных |
|||||||
прямых; |
|
|
|
|
|
|
|
|||
9. |
|
y2 0 – уравнение пары совпадающих прямых. |
||||||||
Приведение уравнений кривых второго порядка к каноническому виду
Укажем, как можно с помощью преобразований координат, рассмотренных в предыдущем параграфе, привести общее уравнение кривой второго порядка
a11x2 2a12xy a22 y2 2a1 y 2a2 y a0 0
к каноническим уравнениям эллипса, гиперболы или параболы, или к случаям их выражения.
С помощью поворота осей координат на некоторый угол α всегда можно избавиться от члена с произведением координат.
Действительно, |
|
|
|
|
|
|
|
|
|
a x 2 2a |
x y a y 2 |
2a x |
2a y a |
0 |
|||||
11 |
|
12 |
22 |
|
|
1 |
2 |
0 |
|
коэффициент которого a будет равен |
|
|
|||||||
|
|
|
12 |
|
|
|
cos2 sin2 |
||
a |
a |
a sin cos a |
|||||||
12 |
22 |
|
11 |
|
|
12 |
|
|
|
Приравнивая коэффициент a |
к нулю, получим |
|
|
||||||
|
|
|
12 |
|
|
|
|
|
|
тригонометрическое уравнение |
cos2 sin2 0 |
||||||||
a |
a |
sin cos a |
|||||||
22 |
11 |
|
|
12 |
|
|
|
|
|
Отсюда получаем |
|
|
|
|
|
|
|
||
|
|
|
tg 2 |
|
2a12 |
. |
|
|
|
|
|
|
a |
a |
|
|
|||
|
|
|
|
|
11 |
22 |
|
|
|
Далее, по формулам тригонометрии, получаем нужные нам значения для sin и cos :
156
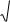
tg 2 |
|
2tg |
|
(здесь можно взять любое из двух |
||
|
|
|
|
|
||
1 tg 2 |
||||||
значений tg ), |
|
|
||||
cos |
1 |
|
|
(здесь можно взять любой знак), |
||
|
|
|
||||
|
|
|
|
|
||
|
1 tg 2 |
|||||
sin cos tg .
Следовательно, уравнение кривой в новых координатах O x y примет вид:
a x 2 |
a |
|
y 2 |
2a x 2a y a 0 |
|
|
||
11 |
22 |
|
1 |
2 |
0 |
|
|
|
Если в уравнении a |
a |
0 , |
то говорят, что это уравнение |
|||||
|
11 |
|
22 |
|
|
|
|
|
определяет линию эллиптического типа; если же a |
a |
0 , |
||||||
|
|
|
|
|
|
11 |
22 |
|
то говорят, что уравнение определяет линию гиперболического
типа и, если один из коэффициентов a |
или a |
равен нулю, |
11 |
22 |
|
то уравнение определяет линию параболического типа. Далее с помощью параллельного переноса системы координат O x y уравнение всегда можно привести к виду:
a x 2 |
a |
y 2 a 0 |
11 |
22 |
0 |
т.е. фактически к каноническому виду.
Из уравнения следует, что мы имеем либо эллипс (если a
11
и a |
одного |
знака, |
а |
a противоположного), |
либо |
мнимое |
||||||
22 |
|
|
|
|
|
0 |
|
|
|
|
|
|
место точек (если |
a |
|
, |
a |
|
, |
a |
имеют один знак), либо одну |
||||
|
|
|
11 |
|
22 |
|
0 |
|
|
|
||
точку |
(если |
a |
и |
a |
|
имеют |
один знак, а |
a 0 ), либо |
||||
|
|
11 |
|
|
22 |
|
|
|
|
0 |
|
|
гиперболу (если a |
и |
|
a |
разных знаков и a |
0 ), либо две |
|||||||
|
|
11 |
|
|
|
22 |
|
|
|
0 |
|
|
пересекающие прямые (если a и |
a разных знаков и a 0 ). |
|||||||||||
|
|
|
|
|
|
|
|
|
11 |
22 |
|
0 |
Если же в уравнении один из коэффициентов a |
и a , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
11 |
22 |
например, a |
обращается в нуль, |
то это уравнение с помощью |
||||||||||
|
22 |
|
|
|
|
|
|
|
|
|
|
|
переноса осей приведется к каноническому уравнению параболы
y 2 px 2 при a |
0 |
или к виду ax 2 d 0 |
при a |
0 , что |
22 |
|
|
22 |
|
дает или две параллельные прямые, или мнимое место точек.
157

Отсюда следует, что всякая кривая 2-го порядка есть либо эллипс, либо гипербола, либо парабола, либо представляет собой их "вырождение".
 Пример Привести к каноническому виду уравнение кривой второго порядка
Пример Привести к каноническому виду уравнение кривой второго порядка
29x2 24xy 36y2 |
82x 96y 91 0 |
и сделать чертеж. |
||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
Здесь a11 29, a12 12, a22 36 . |
|
|
|
|
|
|||||
tg 2 |
|
24 |
|
24 |
, |
24 |
|
|
2tg |
, |
|
29 36 |
|
|
|
tg 2 |
|||||
Поэтому |
|
7 |
|
7 |
1 |
|
||||
12tg 2 7tg 12 0
решая последнее уравнение, получим tg 43 и tg 34
Выбираем: пусть tg 34 , тогда cos 54 .
Выбираем: пусть cos 54 , тогда sin 53 .
И формулы преобразования координат запишутся в виде:
x 54 x 53 y , y 53 x 54 y .
158
Подставляем выражения "старых" координат через "новые" в исходное уравнение кривой и, проделав достаточно громоздкие, но простые преобразования, получаем:
20x 2 45y 2 8x 126y 91 0
или, выделяя полный квадрат по x и y можем записать:
20 x |
1 |
2 |
45 y |
7 |
2 |
180, |
|
|
|
|
|||
|
|
|
|
|
||
|
5 |
|
|
5 |
|
|
отсюда: |
|
|
|
|
|
|
|||
|
|
1 |
|
2 |
|
|
7 |
2 |
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||
|
|
5 |
|
|
|
|
5 |
|
1 |
9 |
|
|
|
4 |
|
|
|||
|
|
|
|
|
|
|
|||
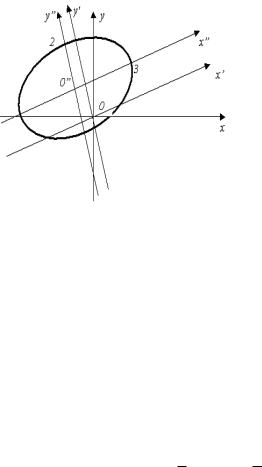
Введем новые координаты x x 15 , y y 75 , и в этих координатах уравнение примет вид
x 2 |
y 2 |
|||
|
|
|
|
1 т.е. данная кривая есть эллипс с полуосями |
2 |
|
2 |
||
3 |
|
2 |
|
|
a 3 и b 2 .
159
Контрольные вопросы по теме «Параллельный перенос»
1.Что такое параллельный перенос системы координат?
2.Приведите формулы связи "старых" и "новых" координат.
3.Приведите формулы связи "старых" и "новых" координат при повороте системы координат без изменения еѐ начала.
4.Объясните методику приведения общего уравнения кривой второго порядка к каноническому виду, используя последовательно поворот системы координат и параллельный перенос системы координат. Какой результат достигается на каждом из этих этапов преобразования системы координат?
Задачи для самостоятельного изучения
1. Выяснить геометрический смысл уравнений:
а) 4x2 y2 0 , б) 4x2 y2 0 ,
в) x2 y2 2x 2 0 , г) x2 y2 6x 8y 25 0 , д) x2 xy 0 , е) y2 16 0 .
2.Поворотом осей координат преобразовать уравнения к каноническому виду и построить кривые:
а) 5x2 4xy 2y2 24 , |
б) 2x2 4xy y2 12 . |
3.Преобразовать уравнения к каноническому виду и сделать чертеж:
а) 3x2 2xy 3y2 4x 4y 12 0 , б) x2 6xy y2 4x 4y 12 0 ,
в) x2 4xy 4y2 20x 10y 50 0 , г) x2 4xy 4y2 6x 12y 8 0 .
160
