
Blatov_lek
.pdf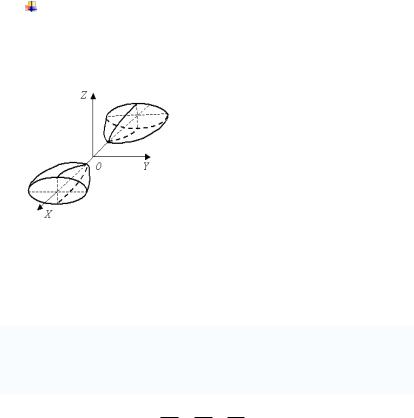
Пример Найти уравнение поверхности вращения
гиперболы |
x2 |
|
y2 |
1вокруг действительной оси. |
|
|||||
a2 |
b2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
Решение Вращение происходит |
вокруг оси Ox , |
|||||||||
|
|
|
|
следовательно, |
|
|
уравнение |
|||
|
|
|
|
поверхности вращения будет |
||||||
|
|
|
|
|
x2 |
|
y2 |
|
z2 |
1 |
|
|
|
|
|
a2 |
b2 |
b2 |
|||
|
|
|
|
|
|
|
|
|||
Такая поверхность носит название двуполостного
гиперболоида вращения.
Различают одно и двухполостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой
оси, а второй – вращением гиперболы вокруг действительной оси.
Двухполостный гиперболоид
Определение Двухполостный гиперболоид –
поверхность, которая в некоторой системе декартовых прямоугольных координат, определяется уравнением
x2 y2 z2 1 a2 b2 c2
где |
|
a,b,c - полуоси гиперболоида . |
|
|||||
|
|
|
|
|
|
|
||
Исследуем с помощью метода параллельных сечений форму |
||||||||
двухполостного гиперболоида. |
|
|||||||
Рассмотрим |
сечение плоскостями, плоскостями OXZ и |
|||||||
OYZ . |
|
|
|
|
|
|
|
|
Сечение плоскостью OXZ определяется |
|
|||||||
x |
2 |
|
z 2 |
1 |
|
|
||
|
|
|
|
|
|
|||
|
2 |
c2 |
|
OX |
||||
a |
|
|
|
гипербола симметричная относительно |
||||
|
0 |
|
|
|
|
|
||
y |
|
|
|
|
|
|||
и OZ .
181
Сечение плоскостью OYZ определяется
y2 |
|
z 2 |
1 |
|
|
|
|
|
|
||
|
c2 |
|
|||
b2 |
|
|
гипербола симметричная относительно OY и |
||
|
|
|
|
|
|
x 0 |
|
|
|
||
OZ
Рассмотрим сечение плоскостями, параллельными плоскости
OXY . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
y2 |
|
1 |
h2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
||||||
В сечении получается |
a2 |
|
|
|
b |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z h |
|
|
|
|
|
|
|
|||||
При |
|
h |
|
c |
плоскость |
|
z c |
|
пересекает двухполостный |
|||||||||||||
|
|
|
|
|||||||||||||||||||
гиперболоид по эллипсу с полуосями |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a* a |
h2 |
1, |
b* b |
|
|
h2 |
1 |
|
|
|||||||||||||
c2 |
|
|
c2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично при рассмотрении сечений эллипсоида с |
||||||||||||||||||||||
плоскостями |
OXZ и OYZ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для обоих гиперболоидов сечения, параллельные оси z - гиперболы (для однополостного гиперболоида может быть пара пересекающихся прямых), сечения, параллельные плоскости
XOY – эллипсы. |
|
|
|
|
|
|
||||||
|
|
Пример Найти уравнение |
поверхности |
вращения |
||||||||
|
x2 |
|
y2 |
|
1вокруг мнимой оси. |
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Решение |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Вращение происходит вокруг оси |
|||||||
|
|
|
|
|
Оу, следовательно, уравнение |
|||||||
|
|
|
|
|
поверхности вращения будет |
|||||||
|
|
|
|
|
|
x2 |
|
y2 |
|
z2 |
1 |
|
|
|
|
|
|
|
a2 |
b2 |
|
||||
|
|
|
|
|
|
|
|
a2 |
|
|||
|
|
|
|
|
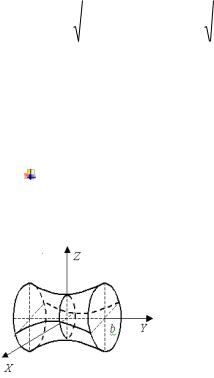
Такая поверхность |
называется |
||||||
|
|
|
|
|
однополостным |
|
гиперболоидом |
|||||
|
|
|
|
|
вращения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
182

Однополосный гиперболоид
Определение Однополосный гиперболоид – поверхность,
которая в некоторой системе декартовых прямоугольных координат, определяется уравнением
x2 y2 z2 1 a2 b2 c2
где a,b,c - полуоси гиперболоида, если они различны.
С помощью метода параллельных сечений исследуем форму однополостного гиперболоида.
Рассмотрим сечение плоскостями, плоскостями OXZ и OYZ .
Сечение плоскостью OXZ определяется
x2 |
|
z 2 |
1 |
|
|
|
|
|
|
||
|
c2 |
|
|||
a2 |
|
|
- гипербола симметричная относительно OX и |
||
|
|
|
|
|
|
y 0 |
|
|
|
||
OZ . |
|
|
|
|
|
Сечение плоскостью OYZ определяется |
|||||
y2 |
|
z 2 |
1 |
|
|
|
|
|
|
||
|
c2 |
|
|||
b2 |
|
|
- гипербола симметричная относительно OY и |
||
|
|
|
|
|
|
x 0 |
|
|
|
||
OZ
Рассмотрим сечение плоскостями, параллельными плоскости
OXY . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x2 |
|
y2 |
1 |
h2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
b2 |
c2 |
|
|
|
||||||||
В сечении получается a2 |
|
|
|
|
|
|||||||||||
|
|
|
h |
|
|
|
|
|
|
|
|
|
||||
|
|
z |
|
|
|
|
|
|
|
|
|
|||||
Плоскость z h пересекает |
гиперболоид |
по эллипсу с |
||||||||||||||
полуосями |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a* a 1 |
h2 |
, |
|
|
b* b 1 |
h2 |
|
, |
||||||||
|
|
|
c2 |
|
||||||||||||
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
||||
183

Аналогично при рассмотрении сечений эллипсоида с плоскостями OXZ и OYZ .
Замечание Однополостный гиперболоид является дважды линейчатой поверхностью (то есть может быть составлена из одних прямых); если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней. Это свойство линейчатости однополостного гиперболоида используется в архитектуре.
Замечание Шуховская башня в Москве является гиперболоидной конструкцией. Она составлена именно из гиперболоидов, образованных прямыми стержнями, выполнена в виде несущей стальной сетчатой оболочки. Расположена в Москве на улице Шаболовка. Построена в 1919—1922г.. великим русским инженером, академиком Владимиром Григорьевичем Шуховым (1853—1939).
Шуховская башня имеет оригинальную изящную сетчатую конструкцию, благодаря чему достигается минимальная ветровая нагрузка, представляющая главную опасность для высоких сооружений. По форме секции башни — это однополостные гиперболоиды вращения, сделанные из прямых балок, упирающихся концами в кольцевые основания. Такие конструкции оказались легкими и прочными. Они часто употребляются для устройства высоких радиомачт, водонапорных башен.
 Пример Найти уравнение поверхности вращения
Пример Найти уравнение поверхности вращения
гиперболы z y2 вокруг оси Oz .
Решение
Поверхность z x2 y2 , получаемая
в результате вращения, называется
параболоидом вращения.
184

Параболоиды
Параболоид может быть охарактеризован как незамкнутая нецентральная (т.е. не имеющая центра симметрии) поверхность второго порядка. Параболоид ― тип поверхности второго порядка.
Эллиптический параболоид
Определение Эллиптический параболоид –
поверхность, которая в некоторой системе декартовых прямоугольных координат, определяется уравнением
2z x2 y2 p q
С помощью метода параллельных сечений исследуем форму эллиптического параболоида.
Рассмотрим сечение плоскостями, плоскостями OXZ и OYZ .
Сечение плоскостью OXZ определяется |
|
|
|
|
||||||||
x2 |
2 pz |
|
|
|
|
|
|
|
|
|
OZ , с |
|
|
|
- парабола симметричная относительно |
||||||||||
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
вершиной в начале координат |
|
|
|
|
|
|
|
|
|
|||
Сечение плоскостью OYZ определяется |
|
|
|
|
||||||||
y2 |
2qz |
|
|
|
|
|
|
|
|
OZ |
|
|
|
|
- парабола симметрично относительно |
|
|||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим сечение плоскостями, параллельными плоскости |
||||||||||||
OXY . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
|
|
|
|
||||
|
|
|
|
|
|
2h |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
В сечении получается p |
|
q |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z h |
|
|
|
|
|
|
|
|
||
Плоскость |
z h пересекает эллиптический параболоид по |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
эллипсу |
с |
полуосями |
a* 2hp, |
b* |
|
2hq |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
185

Аналогично при рассмотрении сечений эллипсоида с плоскостями OXZ и OYZ .
Сечения, параллельные оси Z – параболы, сечения, параллельные плоскости XOY – эллипсы.
Замечание Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.
Замечание Если p q то эллиптический параболоид
представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы.
Гиперболический параболоид
Определение Гиперболический параболоид – поверхность определяемая уравнением
2z x2 y2 p q
Гиперболический параболоид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая уравнением вида
2z x2 y2 p q
|
x |
|
|
y |
|
|
|
x |
|
|
y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
q |
||||||
Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью.
Определение Линейчатая поверхность ― поверхность,
образованная движением прямой линии.
186

Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной
Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».
С помощью метода параллельных сечений исследуем форму эллиптического параболоида.
Рассмотрим сечение плоскостями, плоскостями OXZ и OYZ .
Сечение плоскостью OXZ определяется
x |
2 2 pz |
- парабола симметричная относительно OZ , с |
|||
|
|
|
|||
y 0 |
|
|
|
|
|
вершиной в начале координат |
|||||
Сечение плоскостью OYZ определяется |
|||||
|
|
y2 |
|
h2 |
|
2z |
|
|
|
|
|
|
|
|
|||
|
|
q |
|
p - парабола симметрично относительно |
|
|
h |
|
|
|
|
x |
|
|
|
|
|
OXZ
Рассмотрим сечение плоскостями, параллельными плоскости
OXY . |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
h2 |
|||||
|
|
|
|
|
|
|
2z |
||
|
|
|
|
||||||
В сечении получается |
p |
|
|
q |
|||||
|
|
|
|
|
|
|
|||
|
y h |
|
|
|
|||||
Рассмотрим сечение плоскостями, параллельными плоскости |
|||||||||
OXY . |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
y2 |
|||||
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
|
|||||
В сечении получается |
p |
|
|
q |
|||||
|
|
|
|
|
|
|
|||
|
z h |
|
|
|
|||||
Плоскость z h пересекает гиперболический параболоид по гиперболам.
187
Сечения, параллельные плоскостям OYZ и XOZ – параболы, сечения, параллельные плоскости XOY – гиперболы ( и пара пересекающихся прямых).
Замечание
Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной
188
Лекция 15 Цилиндрические и конические поверхности
Цилиндрические поверхности являются частным случаем линейчатых поверхностей. Цилиндрическая поверхность имеет бесконечно много разнообразных направляющих (изоморфных друг другу).
Характеристикой направляющей кривой, качественно влияющей на цилиндрическую поверхность, является замкнутость: если направляющая кривая замкнута, цилиндрическая поверхность называется замкнутой, и разомкнутой в противоположном случае.
Цилиндрические поверхности
Определение Цилиндрическая поверхность -
поверхность, образованная прямыми (образующими), параллельными некоторой данной прямой L и пересекающими данную линию C (направляющую).
Беря за направляющие цилиндрических поверхностей различные кривые 2-го порядка, лежащие в плоскости OXY , и принимая направление оси OZ за направление образующих этих цилиндров, получаем уравнения цилиндрических поверхностей:
Допустим, что направляющая C задана уравнениями
F (x, y, z) 0Ф(x, y, z) 0
а образующая L задана уравнениями
|
|
X x |
|
Y y |
|
Z z |
||
|
|
|
|
|
|
|||
|
|
m |
|
|
n |
|
p |
|
где X ,Y , Z |
- текущие |
координаты |
точек, принадлежащих |
|||||
образующим, т.е. цилиндрической |
поверхности; x, y, z - |
|||||||
координаты точек, принадлежащих направляющей C . Если из |
||||||||
уравнений |
исключим |
x, y, z , |
то |
получим уравнение |
||||

