Blatov_lek

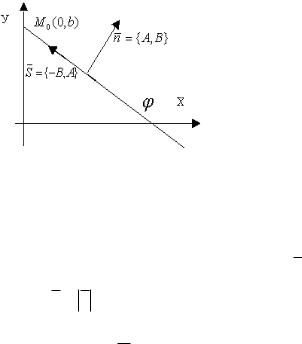
0 , то k 0 - прямая параллельна оси OX ,

2 , то k , прямая перпендикулярна оси OX , не

Каждая прямая, не перпендикулярная к оси ОХ, определяется уравнением

y kx b

b 0 , то y kx - прямая, проходит через начало координат и имеет угловой коэффициент k .

Выясним геометрический смысл коэффициентов k и b .

Найдем точку M 0 пересечения прямой с осью ординат.

Так как абсцисса точки M 0 равна нулю, то ее ордината равна b , т.е. M 0 0,b .

Обозначим через угол между вектором S и осью Ox .

102

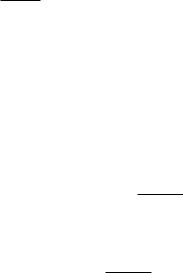
Таким образом, k есть тангенс угла между заданной прямой

угловым коэффициентом.

Очевидно, что уравнением прямой с угловым коэффициентом можно описать любые прямые, кроме прямых, параллельных оси ординат, которые описываются уравнением

x a ,

где a const .

Уравнение прямой проходящей через одну точку с угловым коэффициентом

Пусть точка M x,y лежит на прямой, которая проходит через точку M1 x1,y1 ,

тогда k y y1 , или x x1

y y1 k x x1

уравнение прямой проходящей через одну точку с заданным угловым коэффициентом.

Уравнение прямой, проходящей через две заданные точки

Возьмем произвольные две точки M1 x1,x2 , M 2 x2 ,y2 , тогда

угловой коэффициент находим k y2 y1 x2 x1

или, используя уравнение прямой проходящей через одну точку с заданным угловым коэффициентом, имеем

y y1 y2 y1 x x1 x2 x1

103

или, преобразуя,

-уравнение прямой, проходящей через две заданные

точки

Уравнение пучка прямых с центром в точке M x0 , y0

tg A1B2 A2 B1 A1 A2 B1B2

При решении задач аналитической геометрии важно знать являются ли прямые параллельными, или они перпендикулярны друг другу.

Прямые параллельны, если tg 1 tg 2 - углы наклона к оси ОХ одинаковы или

104

или

A1 A2 B1B2 0 условие перпендикулярности.

Замечание угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.

Пример Выяснить расположение прямых на плоскости

y 2x 1 и y 2x 5 - параллельные прямые

Уравнение в отрезках

Пусть дано уравнение Ax By C 0

где A 0 , B 0 , С 0

преобразуем

Ax By C

или

или

105

ax by 1 - уравнение в отрезках.

Геометрический смыс уравнения в отрезкахл:

a,b - отрезки, которые отсекает прямая от начала

координат.

Нормальное уравнение прямой

Пусть дана прямая, проведем через начало координат прямую, перпендикулярно к данной – нормаль, точка Р – точка пересечения данной прямой с нормалью, α- угол от оси ОХ до направления нормали, p - расстояние от начала координат до

прямой.

Здесь - угол между вектором нормали n и осью Ox

 Замечание В нормальном уравнении прямой сумма квадратов коэффициентов при текущих координатах должна быть равна 1, а свободный член должен быть отрицателен.

 Определение Отклонением точки M * от данной прямой называется число d , если M * лежит по ту сторону прямой,

106

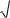
d , когда точка M * и начало координат лежат по разные стороны от прямой, и d , когда точка M * и начало координат лежат по одну сторону от прямой, 0 для точек лежащих на прямой.

Чтобы найти отклонение какой-либо точки M * от некоторой прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки M * .

x* cos y* sin p .

Расстояние от точки до прямой

Приведем общее уравнение прямой к нормальному виду

Ax By C 0

xcos ysin p 0

оба уравнения определяют одну и ту же прямую, следовательно, коэффициенты этих уравнений пропорциональны.

Умножим общее уравнение на множитель

нормирующего множителя противоположен знаку свободного члена нормируемого уравнения.

Для приведения общего уравнения прямой к нормальному виду обе части его умножают на нормирующий множитель, знак выбирают противоположный знаку свободного члена в общем уравнении прямой.

107

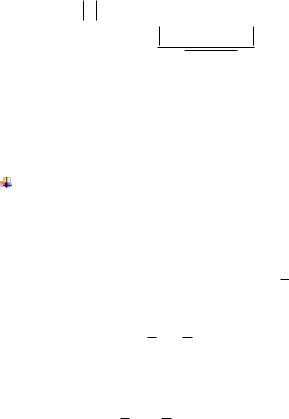
Расстояние от точки до прямой равно модулю отклонения этой точки d

d Ax0 By0 C

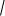A2 B2

Чтобы определить расстояние от точки до прямой, нужно привести уравнение к нормальному виду, взяв левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние.

Пример Найти расстояние от точки A 7, 3 до прямой, заданной уравнением 3x 4y 15 0 .

Решение

поэтому нормирующий множитель равен 15 ,

и нормальное уравнение прямой имеет вид:

53 x 42 y 3 0

Подставив в его левую часть вместо x и y координаты точки A , получим, что ее отклонение от прямой равно

53 7 54 3 3 4,8.

Следовательно, расстояние от точки A до данной прямой равно 4,8.

Контрольные вопросы

1.Напишите известные виды уравнений прямой на плоскости и объясните смысл величин, входящих в эти уравнения.

2.Как вычислить угол между двумя прямыми?

3.Условия параллельности и перпендикулярности двух прямых.

108

уравнения двух других сторон и третьей высоты этого треугольника.

12.Составить уравнения сторон треугольника, если даны одна из его вершин В (- 4; - 5) и уравнения двух высот

5x 3y 4 0 и 3x 8y 13 0 .

13.Определить, при каких значениях " a " и " b " две прямые ax 2y 1 0 , 6x 4y b 0 : а) имеют одну общую

точку; б) параллельны; в) совпадают.

14.Вычислить площадь треугольника, отсекаемого прямой 3x 4y 12 0 от координатного угла.

15.Составить уравнение прямой, которая проходит через точку Р (2; 3) и отсекает на координатных осях отрезки равной длины, считая каждый отрезок от начала координат.

Ответы к задачам для самостоятельного решения

2.а) 2x 3y 7 0 , б) 3x 2y 4 0 ;

3.3x 2y 4 0 ;

4.(2; 1), (4; 2), (- 1; 7), (1; 8);

5.(- 12; 5);

6.M1 10; 5 ;

7.3x 2y 0 ;

8.2x 3y 13 0 ;

110