Blatov_lek

Гиперболический цилиндр:

Пара пересекающихся плоскостей:

Ось цилиндра служит ось OZ.

Цилиндрическая поверхность, образующие которой параллельны оси OZ, а направляющей является эллипс.

Гиперболический цилиндр

 Определение Гиперболический цилиндр – поверхность определяемая уравнением

Ось цилиндра служит ось OZ.

191

Параболический цилиндр

 Определение Параболический цилиндр – поверхность определяемая уравнением

y2 2 px

Сечениями цилиндров являются соответственно эллипсы, гиперболы и параболы.

Параболический цилиндр — цилиндрическая поверхность второго порядка, для которой направляющей служит парабола. Его можно получить при перемещении параболы по прямой. Тогда следом от параболы будет параболический цилиндр. Каноническое уравнение: z = ax2,

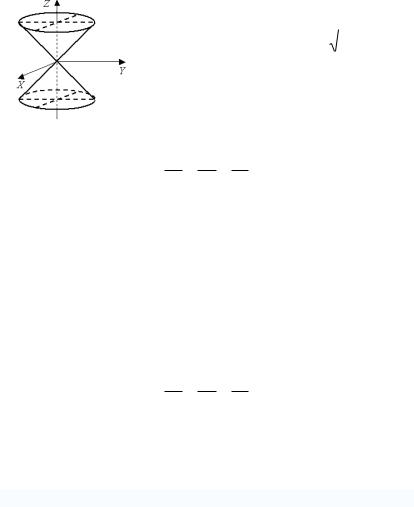
Конические поверхности

 Определение Коническая поверхность- поверхность,

образованная прямыми (образующими конуса), проходящими через данную точку (вершину конуса) и пересекающими данную линию (направляющую конуса).

Пусть направляющая конуса задана уравнениями:

F (x, y, z) 0Ф(x, y, z) 0

где X ,Y , Z - текущие координаты точек образующих. Исключая из уравнений x, y, z , получим уравнение

относительно переменных X ,Y , Z т.е. уравнение конической поверхности.

192

Конус

Пример Найти уравнение поверхности, полученной вращением z y вокруг оси Oz .

 Определение Конус – поверхность определяемая уравнением

x2 y2 z 2 0 a2 b2 c2

Рассмотрим сечение плоскостями, z c

Сечение - эллипс с полуосями a и b Если a b , то конус круглый.

 Определение Мнимый конус – поверхность определяемая уравнением

x2 y2 z 2 0 a2 b2 c2

Это единственная точка (0,0,0)

Поверхность конуса состоит из прямых линий (образующих), проходящих через его вершину и точки эллипса с полуосями a и b , плоскость которого перпендикулярна оси Z .

193

 Определение Аксиома — утверждение, принимаемое истинным без доказательства, а также как «фундамент» для построения доказательств.

Аксиомы линейного пространства

дистрибутивность Перечисленные аксиомы являются естественным

обобщением хорошо известных свойств сложения и умножения чисел, сложения векторов и их умножения на число и т.д.

 Замечание Впервые термин «аксиома» встречается у Аристотеля (384—322 до н. э.) и перешѐл в математику от философов Древней Греции

Следствия аксиом

Из того что существует "нулевой" элемент 0 L , такой, что x 0 x, x L , вытекает , что он единственный

Доказательство

От противного

Пусть существуют два нулевых элемента 0 L , 0 L

195

Следствия аксиом

Из того что существует "противоположный " элемент, такой,

Прибавим к обеим частям первого из этих равенств по вектору x L

Получим x x x 0 x

Но x x 0 отсюда 0 x 0 x т.е. x x .

 Замечание Из аксиомы о существовании нулевого элемента следует, что линейное пространство – непустое множество.

Пример Линейное пространство векторов на плоскости (или в трехмерном пространстве) с обычными операциями сложения векторов и умножения вектора на действительное число. Нулевым элементом является нулевой вектор.

Пример Линейное пространство функций, непрерывных на данном отрезке a, b с обычными операциями сложения

функций и умножения функции на действительное число. Нулевой элемент - функция f (x) 0 .

непрерывны на a, b с обычными операциями сложения

функций и умножения функции на комплексное число. Нулевой элемент - функция f (x) 0 i0

Пример Множество решений однородной системы линейных уравнений является линейным пространством.

196

В силу предложения столбцы-решения системы можно складывать и умножать на число. При этом будут получаться снова решения этой системы. Значит, на множестве решений определены операции сложения и умножения на число. Легко проверить, что эти операции удовлетворяют требованиям из определения линейного пространства.

произвольные комплексные (или действительные) числа.

выполнено при некотором наборе констант, хотя бы одна из которых отлична от нуля.

многочлен, а из алгебры известно, что многочлен тождественно равен нулю тогда и только тогда, когда все его коэффициенты нулевые.

197

Сколько элементов может содержать линейно независимая система в том или ином линейном пространстве?

Очевидно, что в пространстве векторов на плоскости можно указать систему из двух линейно независимых векторов (это могут быть любые 2 неколлинеарных вектора), но уже любые 3 вектора - линейно зависимы. Естественно назвать такое пространство двухмерным.

В то же время в пространстве непрерывных функций, как мы видим, можно указать любое наперед заданное число линейно независимых функций. Такое пространство естественно назвать

размерность n (или, n-мерно), если в нем найдется n линейно

независимых элементов, но любые (n+1) элемент линейно

зависимы.

 Определение Линейное пространство называется

бесконечномерным, если в нем можно указать любое наперед

заданное число линейно независимых элементов.

Пусть теперь L - n-мерное линейное пространство. По определению, в нем существует набор линейно независимых

элементов u1 , u2 , , un .

Если f - произвольный элемент из L, то f , u1 , u2 , , un система линейно зависима, т.к. содержит (n+1) элемент. Значит,

т.е. элемент f оказался представленным в виде линейной комбинации элементов линейно независимой системы.

Убедимся, что такое представление единственно.

198

В самом деле, пусть элемент f можно представить двумя способами в виде линейной комбинации элементов системы:

В правой части мы получим линейную комбинацию элементов линейно независимой системы.

Из равенства этой линейной комбинации нулю следует равенство нулю всех коэффициентов.

элемента f оказались совпадающими.

Мы пришли к следующему выводу: любой элемент n- мерного линейного пространства можно представить (причем единственным способом) в виде линейной комбинации произвольных n элементов, образующих линейно независимую систему.

Этот факт весьма важен: в самом деле, n элементов линейно независимой системы в n-мерном пространстве оказываются теми "кирпичиками", из которых можно сложить абсолютно любой элемент пространства.

В силу важности этого факта введем специальное понятие - базис линейного пространства.

 Определение Система элементов линейного пространства называется базисом этого пространства, если любой элемент этого пространства можно единственным образом представить в виде линейной комбинации элементов данной системы.

Как мы убедились, в n-мерном пространстве любая линейно независимая система из n элементов образует базис.

Естественно поставить вопрос: справедливо ли аналогичное утверждение для бесконечномерных пространств, и что вообще представляет собой базис бесконечномерного пространства?

Само по себе сформулированное выше определение базиса никак не привязано к размерности пространства, поэтому

199

формально такое определение годится и для бесконечномерного пространства.

 Определение В n-мерном линейном пространстве L любая совокупность (система) n линейно независимых векторов называется базисом

x L существуют числа x1, x2 ,..., xn :

x x1e1 x2e2 ... xnen x1, x2 ,..., xn .

Это разложение вектора по базису.

 Теорема В данном базисе координаты вектора определены однозначно.

Доказательство(от противного):

Пусть в базисе e1 два набора чисел для вектора x

xi xi

Пример Базисы в линейном пространстве:

L R4 ; a 1, 2 , 3 , 4

a 1e1 2e2 3e3 4e4

200