Blatov_lek

Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией.

Пусть эти столбцы задают значения свободных неизвестных системы.

Тогда базисные неизвестные будут однозначно определяться для выбранных свободных неизвестных из системы по правилу

71

11.В чем заключается идея метода Гаусса?

12.Какие преобразования матриц называются элементарными?

13.Какие системы являются эквивалентными?

14.Как контролируются полученные результаты решения системы?

Задачи для самостоятельного решения

Исследовать, имеют ли решения приведенные ниже системы. В случае наличия решений указать их число. Используя метод Крамера, найти решения систем 1, 2, 6.

x1 3x2 5x3 7x4 9x5 1 5. x1 2x2 3x3 4x4 5x5 2

2x1 11x2 12x3 25x4 22x5 4

Решить системы 2 и 6 матричным методом и системы 2, 4, 6 методом Гаусса.

73

Ответы к задачам для самостоятельного решения

Собственные значения и вектора линейного оператора

В электро-радиотехнических устройствах собственные значения матриц определяют характеристические постоянные времени и режимы работы этих устройств. Все это говорит о практической важности задач на нахождение собственных значений.

 Определение Ненулевой вектор X , удовлетворяющий соотношению

f(X) λX

называется собственным вектором, а соответствующее число λ

-собственным значением линейного оператора f .

Вматричном виде это соотношение можно записать в виде

A X λX

или

A λE X 0

Однородная система линейных уравнений имеет нетривиальное решение при условии

A λE 0

Любой ненулевой вектор-решение есть собственный вектор, соответствующий собственному числу λ.

Раскрывая этот определитель, получим характеристический многочлен матрицы А .

 Определение Уравнение

A λE 0

называется характеристическим уравнением матрицы А .

74

 Замечание Таким образом, собственные значения

представляет собой полином (многочлен) n -ой степени от

и называется характеристическим полиномом матрицы A .

Легко видеть, что членом, имеющим относительно

A E 0 .

 Замечание Одному собственному значению может соответствовать несколько линейно независимых собственных векторов.

Пример Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе

75

x - собственный вектор, а это значит, что однородная система уравнений имеет ненулевой решение. Это эквивалентно, определитель системы равен нулю.

Решение Вычислим определитель матрицы A

76

Свойства собственных чисел и собственных векторов

1. Если выбрать базис из собственных векторов x1, x2 , x3 , соответствующих собственным значениям 1, 2 , 3

матрицы A , то в этом базисе линейное преобразование имеет матрицу диагонального вида:

2.Если собственные значения преобразования различны, то соответствующие им собственные векторы линейно независимы.

3.Если характеристический многочлен матрицы A

имеет три различных корня, то в некотором базисе матрица A имеет диагональный вид.

78

Лекция 6 Скалярное произведение векторов

 Определение Скалярное произведение двух векторов -

число, равное произведению длин этих векторов на косинус угла между ними, т.е.

a b a, b ab cos a,b

Из определения следует формула для нахождения косинуса угла между векторами:

cos a b ab

где - угол между векторами.

 Определение Проекция вектора a на вектор b -

скалярная величина

prb a a cos

В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевое значения.

Теперь можно написать

a b = b prb a = a prab

Из определения скалярного произведения следует, что если векторы ортогональны, то

a b 0

(условие ортогональности ненулевых векторов), обозначение: a b .

 Замечание Проекция вектора на вектор есть число, оно может быть положительным, отрицательным и нулем.

Основные свойства проекций

1. Проекция суммы векторов равна сумме проекций pru a1 an pru a1 pru an

2. При растяжении вектора a в раз его проекция растягивается тоже в раз

79

pru a pru a

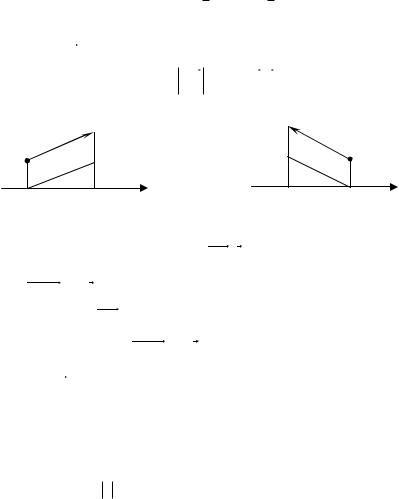
3. Проекция вектора на ось равна произведению длины вектора AB на косинус угла между вектором и осью:

x AB cos(AB,e) .

prL AB | A1B1 | | A1B2 | cos(180 ) | A1B2 | cos | AB | cos

Свойства скалярного произведения

1.a,b = b,a

2.a,a = a 2

3.a + b,c = a,c + b,c

4.(αa,b) α(a,b) , α- вещественное число

5. если a 0,b 0 , и a,b = 0 , то a b

i i = j j = k k = 1

Скалярные произведения ортов i j = j k = k i = 0

80