
Blatov_lek
.pdf9. 7x 2y 12 0; |
|
|
|
|
|
|
||
10. |
a) 5x y 28 0 |
, |
б) 2x 3y 18 0 , |
в) |
0 , г) |
|||
|
4x 3y 11 0 ; |
|
|
|
|
|
|
|
11. |
BC: |
x y 2 0 |
CA: 3x 2y 13 0 , |
CN: |
||||
|
4x y 3 0 |
|
|
|
|
|
|
|
12. |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
13. |
а) при |
, б) при |
a 3 и arctg |
16 |
, в) |
при a 3 и |
||
|
||||||||
|
|
2 |
|
11 |
|
|
||
b 2 ;
14.6;16;3x 4y 22 0
111
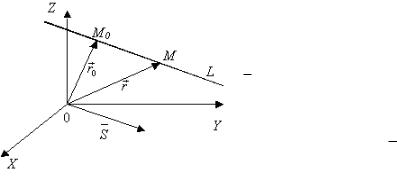
Лекция 9 Прямая линия в пространстве
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Прямую линию можно определить как геометрическое место точек, принадлежащих одновременно двум непараллельным плоскостям.
Уравнение прямой как линии пересечения двух плоскостей
Пусть уравнения плоскостей P1 и P2 заданы, тогда система уравнений
A1 x B1 y C1 z D1 0A2 x B2 y C2 z D2 0
определяет прямую линию, и систему |
называют |
общим |
|||
уравнением прямой линии. |
|
|
|
|
|
Прямая |
линия |
будет |
|||
полностью определена, если |
|||||
на |
ней |
фиксировать |
точку |
||
M 0 |
x0 , y0 , z0 |
|
и |
вектор |
|
S m,n,p , параллельный этой прямой. Точку M 0 иногда называют начальной
точкой, а вектор S -
направляющим вектором
прямой.
Определение Каждый, не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется
направляющим вектором этой прямой.
Любой из направляющих векторов задает направление прямой a l, m, n .
112

Параметрическое уравнение прямой
Пусть r0 - радиус-вектор начальной точки M 0 , r - радиусвектор текущей точки M прямой.
Тогда вектор M0M r r0 коллинеарен направляющему вектору прямой S , следовательно, r r0 M0M t S,
где t |
- некоторое число, называемое параметром. |
||||||||||||||||
Уравнение |
называется |
векторным |
|
параметрическим |
|||||||||||||
уравнением прямой. |
|
|
|
|
|
|
|
|
|
||||||||
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r x, y, z , r0 |
x0 , y0 , z0 , |
|
|
m,n,p , |
|||||||||||
|
|
S |
|||||||||||||||
то можно перейти к уравнения в координатном виде: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x x0 |
mt |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
nt . |
|
|
|
|||
|
|
|
|
|
|
|
|
|
y y0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
z0 |
pt |
|
|
|
|||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|||||
- параметрическое уравнение прямой, проходящей через |
|||||||||||||||||
точку M 0 x0 ,y0 ,z0 в направлении вектора a l,m, n . |
|||||||||||||||||
Изменяя значения t , |
можно получить координаты любой |
||||||||||||||||
точки, лежащей на прямой. |
|
|
|
|
|
|
|
||||||||||
Каноническое уравнение прямой |
|
|
|
|
|
|
|||||||||||
Преобразуем |
параметрические |
уравнения к следующему |
|||||||||||||||
|
x x0 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y y |
0 |
|
t. |
|
|
|
|
|
|
|
|
|
|||||
виду |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
z0 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x x0 |
|
y y0 |
|
z z0 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|
p |
|
|
|
113
Уравнения |
|
называются |
|
|
|
каноническими уравнениями |
||||||||||||||||||||||
прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Углы, образуемые прямой с осями координат, находят по |
||||||||||||||||||||||||||||
формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
cos |
|
|
|
|
l |
|
|
|
|
|
|
|
|
, cos |
|
|
|
|
|
m |
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
l 2 |
m2 |
n2 |
|
|
|
|
|
|
l 2 m2 n2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
cos |
|
|
|
|
|
|
n |
|
|
|
|
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
l 2 m2 |
n2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Уравнение прямой, проходящей через две точки |
|
|
||||||||||||||||||||||||||
В качестве |
направляющего |
вектора |
|
|
|
рассмотрим вектор |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a M1M2 , отсюда l x2 |
x1, m y2 |
y1, n z2 z1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
x x1 |
|
y y1 |
|
|
z z1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x |
2 |
|
|
|
y |
2 |
y |
|
z |
2 |
|
|
z |
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
||||||||
Переход от общих уравнений прямой к каноническим
Чтобы перейти от общих уравнений прямой к каноническим, нужно найти какую-либо точку M1(x1,y1,z1) на прямой.
Пусть прямая L задана общим уравнением
A1 x B1 y C1 z D 0
A2 x B2 y C2 z D2 0
Координаты точки M1(x1,y1,z1) находятся как решение системы уравнения, задав одной из координат произвольное
значение. |
|
|
|
|
||||||||||||||
За направляющий вектор |
||||||||||||||||||
s |
|
|
можно взять вектор |
|||||||||||||||
произведения нормальных векторов. |
|
|
|
|
|
|||||||||||||
|
|
1 A1 , B1 , C1 |
|
|
|
|
2 A2 , B2 , C2 : |
|||||||||||
|
N |
и |
N |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
||||||
s |
|
1 |
|
2 |
A1 |
|
|
|
|
|
|
|
|
|||||
N |
N |
B1 |
|
C1 |
|
|||||||||||||
|
|
|
|
|
|
|
A2 |
B2 |
|
C |
|
|||||||
114

Пример Уравнение прямой задано в общем виде
x y z 4 0
2x y 4x 5 0 . Необходимо записать уравнение прямой в каноническом виде.
Решение
Для записи уравнений нужно знать координаты какой-либо
точки M 0 на прямой и координаты какого-либо направляющего
вектора S прямой. Находим координаты точки M 0 x0 ,y0 ,z0 .
Для этого одну из координат задаем произвольно (так, чтобы оставшаяся система двух уравнений с двумя неизвестными
имела единственное решение), скажем, z0 0 . После этого решаем систему относительно x0 и y0
|
x0 y0 0 4 0 |
|
|
|
|
|
|
|
|
1 |
|
13 |
|
|
|
|||||||||||
|
|
|
0 5 |
, M |
0 |
|
; |
|
|
|
;0 . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2x0 y0 4 |
|
0 |
|
|
|
|
|
|
3 3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
определения |
вектора |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
нам |
нужны |
координаты |
||||||||||
|
|
|
|
|
|
|
|
|
|
еще одной точки M1 на |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
прямой, тогда в качестве |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
направляющего |
|
|
вектора |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
можно взять вектор M0M1 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
|
|
|
|
|
вычисления |
|||||
|
|
|
|
|
|
|
|
|
|
координат |
|
|
|
M1 |
берем, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
например |
|
|
|
|
|
|
|
|
|
|||||||
z1 1, а x1 и y1 находим из решения системы |
|
|
|
|
||||||||||||||||||||||
x1 y1 1 4 0 |
, M |
|
2 7 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2x1 y1 4 1 5 0 |
|
|
|
; |
|
;1 . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тогда |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S M0 M1 1; |
|
|
;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Канонические уравнения прямой имеют вид
115

|
|
1 |
|
|
13 |
|
|
|
|||
x |
|
|
|
|
y |
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
3 |
|
3 |
|
|
|||||
1 |
|
|
|
4 |
|
|
1 |
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|
||
Один из направляющих векторов можно было найти и как векторное произведение нормальных векторов плоскостей, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
k |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
S |
1 n1 n2 |
1 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
4 |
|
|
|
||||||
|
|
Пример Даны канонические уравнения прямой |
|
||||||||||||||||||||||
x 1 |
|
y 1 |
|
|
z 3 |
. Необходимо перейти к общим уравнениям. |
|||||||||||||||||||
1 |
|
|
|
|
|
||||||||||||||||||||
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Записываем данные уравнения в виде системы |
|
|
|||||||||||||||||||||||
x 1 |
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
2 |
, |
|
|
2x 2 y 1 |
|
|
2x y 1 0 |
|||||||||||||
|
|
|
|
|
|
z 3 |
|
|
, |
|
z 4 |
. |
|||||||||||||
x 1 |
|
|
|
|
|
x 1 z 3 |
|
|
x |
0 |
|||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Последняя система и дает ответ.
Взаимное расположение прямых в пространстве
Определение Углом между двумя прямыми в пространстве будем называть любой из углов, образованных двумя прямыми, проведенными через произвольную точку пространства параллельно данным прямым.
Следовательно, угол между двумя прямыми - это угол между их направляющими векторами, т.е.
|
|
|
|
|
|
|
|
2 |
|
|
|
|
m1m2 n1n2 p1p2 |
|
|
|
|||||
cos |
|
|
S1 |
S |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
S1 |
S |
2 |
2 |
2 |
2 |
|
2 |
2 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
n1 |
p1 |
|
m2 |
n2 |
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
116

Условие перпендикулярности двух прямых
- это условие перпендикулярности их направляющих векторов:
S1 S2 m1m2 n1n2 p1p2 0 ,
Условие параллельности двух прямых - это условие параллельности (коллинеарности) их направляющих векторов:
|
m1 |
|
n1 |
|
p1 |
|
|
m2 |
n2 |
p2 |
|||
|
|
|
||||
Замечание Выделим особо тот частный случай, когда |
||||||
одна из плоскостей в системе |
есть плоскость Oxy , и, |
|||||
следовательно, рассматриваемая прямая лежит в координатной плоскости Oxy . В этом случае система может быть записана в
z 0 |
. |
|
виде: |
|
|
Ax By |
D 0 |
|
Рассмотрим |
вектор n A, B,0 . Он |
расположен в |
плоскости Oxy , перпендикулярен к плоскости |
Ax By D 0 |
|
и, следовательно, перпендикулярен к прямой, определяемой системой.
Поскольку далее будем рассматривать только точки плоскости Oxy , то третьи координаты точек и векторов не будем записывать, всегда подразумевая, что они равняются
нулю. Как |
уже |
отметили, уравнению Ax By D 0 |
в |
плоскости |
z 0 |
соответствует прямая. Поэтому |
в |
аналитической геометрии на плоскости уравнение |
|
||
|
|
Ax By D 0 |
|
называют общим уравнением прямой.
Замечание Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой s перпендикулярен Ox , и , m 0 .
Следовательно, параметрические уравнения прямой примут
x x1,
вид y y1 tn,z z1 tp.
117

Исключая из уравнений параметр t , получим уравнения
прямой в виде |
|
|
|||
x x1 0, |
|
||||
|
|
|
z z1 |
|
|
y y1 |
|
. |
|||
|
n |
p |
|||
|
|
||||
|
|
|
|||
Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде
x x1 |
|
y y1 |
|
z z1 |
. |
|
|
|
|||
0 |
|
n |
|
p |
|
Таким образом, если в знаменателе одной из дробей стоит
нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям
x x |
|
y y1 |
|
z z1 |
|
|
|
||
0 |
0 |
|
p |
|
соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .
Пример Составить канонические и параметрические |
||||||||||||||||
уравнения прямой, проходящей |
через |
точку |
M1 1;0;2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параллельно вектору s 2i |
3j. |
|
|
|
|
|
|
|
|
|
|
|||||
Решение |
|
|
|
|
|
|
|
|
|
|
||||||
Канонические уравнения: |
x 1 |
|
y |
|
|
z 2 |
. |
|
|
|
||||||
|
3 |
|
|
|
|
|
||||||||||
2 |
|
|
|
0 |
|
|
|
|
|
|||||||
|
|
|
|
|
x 2t 1, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметрические уравнения: y 3t, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2. |
|
|
|
|
|
|
|
|
|||
Пример Найдите точку, симметричную данной |
||||||||||||||||
M 0;3; 2 относительно прямой |
x 0.5 |
|
y 1.5 |
|
z 1.5 |
. |
||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
1 |
1 |
|
|||
Решение |
|
|
|
|
|
|
|
|
|
|
||||||
Составим уравнение плоскости |
|
перпендикулярной l . |
||||||||||||||
n s 0, 1,1 . |
|
|
|
|
|
|
|
|
|
|
||||||
118
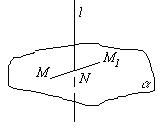
Следовательно, |
:0 x 0 y 3 z 2 0 |
или |
y z 1 0 . |
|
|
Найдѐм точку пересечения прямой l и :
x 0.5 |
|
y 1.5 |
|
z 1.5 |
|
|
x 0.5, |
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
t, |
y t |
1.5, |
|
|
|
|
1 |
|
|
|||||||||
|
0 |
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
z t 1.5, |
|||
y z 1 0. |
|
|
|
|
|
t 1.5 t 1.5 1 0. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0.5, |
|
|
|
|
|
|
|
|
|
|
||||
|
0.5, |
|
|
|
|
|
|
|
|
|
|
|||
y |
|
|
|
|
|
|
|
|
|
|
||||
|
0.5, |
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
|
|
|
|
|
|
|
|
|
|||
t 1. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, N 0.5; 0.5;0.5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть искомая точка M1 имеет координаты M1 x, y, z . |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||
Тогда очевидно равенство |
векторов |
|
|
MN NM1 , , |
т.е. |
|||||||||
0.5;2.5;2.5 x 0.5; y 0.5; z 0.5 . Откуда x 1, y 2, z 3 |
||||||||||||||
или M1 1;2;3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения
1. |
Составить канонические уравнения прямой, проходящей |
|||||||||||
|
через точку |
M 2;0;3 |
|
|
параллельно: |
а) |
вектору |
|||||
|
a 2; 3;5 , , |
б) прямой |
|
x 1 |
|
y 2 |
|
z 1 |
, |
в) оси |
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
5 |
|
2 |
|
1 |
|
||
|
Ox . |
|
|
|
|
|
|
|
|
|
|
|
2. |
Написать канонические и |
|
параметрические уравнения |
|||||||||
|
x 2 y 3z 4 0 |
|
|
|
|
|
|
|
|
|||
|
прямой |
|
|
|
. |
|
|
|
|
|
|
|
|
3x 2 y 5z 4 |
0 |
|
|
|
|
|
|
|
|
||
119
|
|
|
|
|
|
|
|
|
|
|
|
3x 2 y z 1 0 |
|
|||
3. |
Спроецировать |
прямую |
|
|
|
|
|
на |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2x 3e 2z |
2 0 |
|
||
|
плоскость x 2y 3z 5 0. |
|
|
|
|
|
||||||||||
4. |
Через |
точку |
|
М |
(2; - |
|
3; |
1) провести |
прямую, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 y z 1 0 |
|
|
||
|
перпендикулярную |
прямым |
|
|
|
|
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2x y 4z 2 |
0 |
|||
|
3x 2z 6 0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3z |
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
x y |
3 0 |
|
|
|
|
|
|
|
|
|
|||||
5. |
В плоскости XOZ найти прямую, перпендикулярную к |
|||||||||||||||
|
прямой |
|
x 2 |
|
y 1 |
|
z 5 |
|
и проходящую через начало |
|||||||
|
|
|
|
2 |
|
|||||||||||
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
||||
|
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x 2z 1 0 |
|
|
|
||
6. |
Найти |
угол между |
прямой |
|
|
и |
прямой, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
y 2z 1 0 |
|
|
|
||
|
проходящей |
через |
начало |
координат и |
через |
точку |
||||||||||
|
M 1; 1; 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. |
Написать уравнения |
прямой, |
проходящей |
|
через |
точку |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2 y z 4 0 |
||||
|
M 4;3;0 и параллельной прямой |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2x y z 0 |
|
|||
8.Написать уравнение перпендикуляра, опущенного из точки M 2; 3;4 на ось OY .
9.Через точку M 2; 5;3 провести прямую:
а) параллельную оси OZ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) параллельную прямой |
|
x 1 |
|
y 2 |
|
z 3 |
; |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
6 |
9 |
|
|
|
||||||
|
|
|
|
|
|
2x y 3z 1 0 |
. |
|
|||||||||||||
в) параллельную прямой |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
5x 4 y z |
7 |
0 |
|
||||||||||||
10. Проверить, пересекаются ли прямые: |
|
|
|
||||||||||||||||||
а) |
x 1 |
|
y 7 |
|
z 5 |
и |
|
x 6 |
|
|
y 1 |
|
|
z |
; |
|
|||||
2 |
1 |
4 |
|
|
3 |
|
|
2 |
1 |
|
|
|
|||||||||
120
