Blatov_lek

 Замечание Значение ранга матрицы не может превышать меньшей из ее размерностей.

Пример Вычислить ранг единичной матрицы 3-го порядка.

 Определение Базисный минор матрицы - всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы.

Ранг матрицы не изменится от следующих преобразований,

называемых элементарными преобразованиями матрицы.

Элементарные преобразования матрицы

-замена строк столбцами, а столбцов соответствующими строками;

-перестановка строк матрицы;

-вычеркивание строки, все элементы которой равны нулю;

-умножение строки на число, отличное от нуля;

-прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число.

Пример Элементарные преобразования – перестановка строк матрицы

меняются местами первая и третья строки.

Ранг матрицы не меняется

41

Пример Элементарные преобразования прибавление к одной строке матрицы другой ее строки, умноженной на число.

.

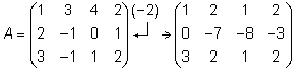Символ, стоящий у первоначальной матрицы, показывает, что ко второй строке матрицы прибавляется первая, умноженная на (–2).

Пример Элементарные преобразования умножение строки матрицы на ненулевое число

.

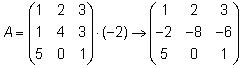Аналогично определяются элементарные преобразования столбцов матриц.

Подчеркнем, что сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.

 Определение Две матрицы A и B называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований.

Записывается A ~ B .

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической.

 Замечание Для матриц большой размерности непосредственное вычисление всех миноров затруднительно.

42

Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже

aii равны 0), воспользовавшись операциями, не изменяющими

ранг матрицы эквивалентными преобразованиями. Действительно, любая из этих операций переводит нулевые

миноры в нулевые, а ненулевые – в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.

Пример Вычислить ранг матрицы.

Решение

Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице A эквивалентные преобразования.

Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0.

Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:

Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:

43

После вычеркивания нулевых строк получим матрицу размерности 2 5 для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2 :

Системы m линейных уравнений с n неизвестными

 Определение Системой m линейных уравнений с n

неизвестными называется система вида

обозначает номер уравнения, а второй j – номер неизвестного,

при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы

44

данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,c2 cn вместо

соответствующих неизвестных x1, x2 xn .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1.Система может иметь единственное решение.

2.Система может иметь бесконечное множество решений.

3.Система вообще не имеет решения.

 Определение Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Назовем расширенной матрицей системы матрицу вида

.Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных.

45

Пример

x1 x2 1,2x1 2x2 2,3x1 3x2 3

система из трех уравнений с двумя неизвестными имеет

Решение

Система из двух уравнений с тремя неизвестными, решений не имеет, то есть является несовместной.

Ответ на вопрос о совместности произвольной системы уравнений дает теорема Кронекера-Капелли.

Капелли Альфредо [1855 – 1910 итальянский математик. Леонид Кронекер (1823–1891) - немецкий математик;

основные труды по алгебре и теории чисел.

Лекции Кронекера по теории чисел пронизаны идеей необходимости арифметизации математики. По его убеждению, основой математики должно быть число, а основой всех чисел – натуральное число, а потому в математике не существует ничего, кроме того, что может быть представлено в виде конечного ряда положительных целых чисел.

Известно его заявление на съезде в Берлине в 1886:

«Целые числа сотворил Бог, а все прочее – дело рук человеческих».

 Теорема (теорема Кронекера-Капелли)

Система линейных уравнений совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной

матрицы A* .

RgA RgA* .

Доказательство

46

1) Необходимость:

Пусть система совместна и c1,c2 cn — ее решение. Тогда

комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора.

Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой

определитель, то есть r A1 r A .

2) Достаточность:

Если r A1 r A ,то любой базисный минор матрицы A

является и базисным минором расширенной матрицы.

Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы

A .

Если обозначить коэффициенты этой линейной комбинации cn , то эти числа будут решением системы, т.е. эта

система совместна. Теорема доказана.

 Замечание Теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы.

Поэтому, обычно вместо того, чтобы находить RgA и

RgA* , ищут решение системы.

Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.

47

Пример Определить совместность системы линейных

уравнений:

RgA* 3 Система несовместна. Ответ: решений нет.

48

Пример

Определить совместность системы линейных уравнений.

49

Общий порядок решения системы общего вида

1. Необходимо определить совместность системы, т.е. определить ранги матрицы системы A и расширенной

матрицы AB . Из теоремы Кронекера-Капелли следует, что если

ранги этих матриц не совпадают, то система не совместна и нет смысла ее решать. Если же ранги матриц A и AB равны, то

система совместна.

2. Для совместных систем линейных уравнений справедливы следующие теоремы:

-Если ранг матрицы совместной системы равен числу переменных, т.е. r n , то система имеет единственное решение.

- Если ранг матрицы совместной системы меньше числа переменных, т.е. r n , то система неопределенная и имеет бесконечное множество решений.

50