
Blatov_lek
.pdf
Ответы к задачам для самостоятельного изучения
1.а) две прямые y 2x , б) точка (0,0) , в) мнимая окружность, г) точка (3,4) , д) две прямые x 0 , y x , е) две прямые y 4 ;
|
|
x |
2 |
|
y2 |
1, б) |
X |
2 |
|
|
Y 2 |
1; |
|||||
2. |
а) |
1 |
|
1 |
|
|
1 |
|
|
1 |
|
||||||
24 |
4 |
|
24 |
4 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2 |
|
|
y2 |
1, б) |
|
x |
2 |
|
|
y2 |
1, |
|||
3. |
а) |
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|||||
8 |
|
4 |
|
|
8 |
|
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. в) y12 2
 5x1 , г)две прямые x 2y 3 1
5x1 , г)две прямые x 2y 3 1
161
Лекция 13 Полярная система координат
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Основная заслуга в создании метода координат принадлежит французскому математику Рене Декарту. Он стал основателем аналитической геометрии, в которой геометрические задачи переводились на язык алгебры при помощи метода координат.
Рене Декарт (1596 -1650) — французский математик, философ, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики. Открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637)стало революцией в геометрии. Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры.
Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями.
Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трѐхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке
Кроме прямоугольной или декартовой системы координат часто используется полярная система координат.
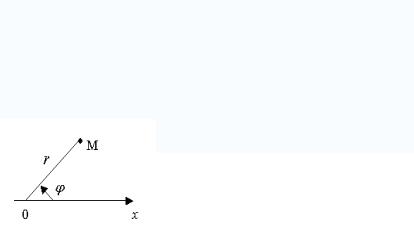
Возьмем на плоскости направленную прямую Ox и на ней точку O .
162
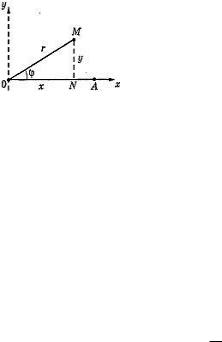
Положение точки M на этой плоскости определяется двумя числами: ее расстоянием r от взятой нами точки O образуемым отрезком OM с положительным направлением прямой Ox . Отсчет углов обычно ведется в направлении, противоположном движению часовой стрелки.
Числа r и называются полярными координатами точки M , причем r называется радиус-вектором, - полярным углом. Прямая Ox называется полярной осью, а
точка O - полюсом полярной системы координат.
Определение Полярная система координат –система координат, ставящая в соответствие каждой точке на
плоскости пару чисел r, , определена заданием некоторой
точки O , называемой полюсом, луча ОМ, исходящего из этой точки, называемого полярной осью, и масштаба для измерения
длин.
Замечание Радиус-вектор r |
(как |
|||||
расстояние) |
- |
всегда |
|
величина |
||
положительная, |
|
а |
угол |
может |
||
изменяться от |
0 |
до |
2 |
и |
далее |
до |
бесконечности. |
|
|
|
|
|
|
Координатные линии полярной системы |
|
|
|
|
||
концентрические окружности |
с |
центром |
в точке |
O |
||
r const |
const . |
|
|
|
||
лучи, выходящие из точки O |
|
|
|
|||
Если полюс полярной системы совпадает с началом прямоугольной системы координат, а полярная ось - с осью абсцисс, то прямоугольные координаты точки M выражаются через ее полярные координаты следующим образом:
Полярные координаты точки M выражаются через ее декартовы координаты такими формулами:
r2 x2 y2
tg yx
163
Декартовы координаты выражаются через полярные координаты такими формулами
x r cosy r sin
Определяя величину и имея в виду, что |
r 0 , |
видим, |
что |
||||||||||||||||||||||||
знак sin |
y |
должен быть одинаков со знаком |
|
y , |
|
а знак |
|||||||||||||||||||||
r |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos |
x |
|
- со знаком x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример Уравнение окружности с центром в полюсе и |
|||||||||||||||||||||||||||
радиуса R |
|
|
- R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример Декартовы координаты точки M (1; 1) . Каковы |
|||||||||||||||||||||||||||
полярные координаты этой точки? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
r |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
7 |
|
|
||||||||
Так как |
|
2 , tg 1, |
т.е. |
|
равно |
или |
|
, но |
|||||||||||||||||||
|
|
4 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||
поскольку |
y 0 , |
то и sin 0 . |
Следовательно |
|
|
полярные |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
7 |
|
|||||
координаты точки M будут r |
|
2, |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
, т.е. M |
2; |
|
|
|
. |
||||||||||||||||||||
|
4 |
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||
Пример Написать уравнение прямой |
x 3 в полярной |
||||||||||||||||||||||||||
системе координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение x r cos , то r cos 3 |
или r |
|
3 |
|
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
cos |
|
|
|
|
|
|
|||||||||||||||||||||
Пример Построить кривую, зная, что полярные |
|||||||||||||||||||||||||||
координаты |
ее |
точек |
|
удовлетворяют |
|
уравнению |
|||||||||||||||||||||
|
|
|
|
|
|
|
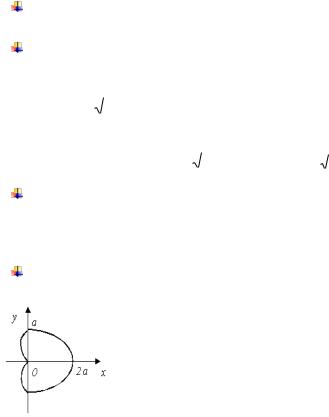
r a 1 cos |
, a 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Решение |
r a 1 cos , a 0 |
-эта |
||||||||||||||||||
|
|
|
|
|
|
|
кривая называется кардиоида. Чтобы |
||||||||||||||||||||
|
|
|
|
|
|
|
начертить эту кривую, нужно давать |
||||||||||||||||||||
|
|
|
|
|
|
|
последовательно |
значения от |
|
0 |
до |
||||||||||||||||
|
|
|
|
|
|
|
(с некоторым шагом) |
и определять |
|||||||||||||||||||
по ее уравнению соответствующие значения r .
164
Каждой из полученных пар чисел r, соответствует в
плоскости полярной системы координат единственная точка. Построив и соединив их плавной линией, получим кардиоиду.
Цилиндрическая система координат |
|
|
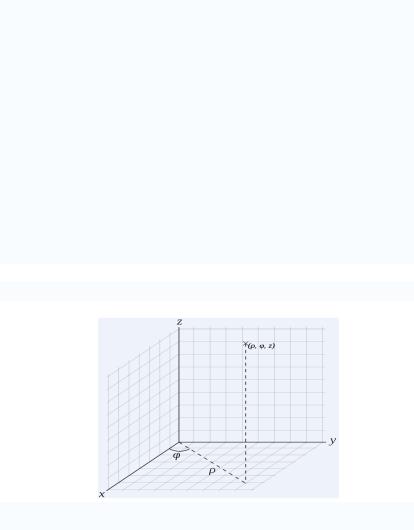
Определение |
Цилиндрической |
системой |
координат называют трѐхмерную систему координат, являющуюся расширением полярной системы координат путѐм добавления третьей координаты (обычно обозначаемой z), которая задаѐт высоту точки над плоскостью.
Точка P даѐтся как , , z рекомендует использовать международный стандарт ISO 31-11.
Втерминах прямоугольной системы координат:
0 — расстояние от O до P', ортогональной
проекции точки P на плоскость XY. Или то же самое, что расстояние от P до оси Z.
0 3600 — угол между осью X и отрезком OP'.
z равна аппликате точки P
Некоторые математики используют , , z .
165

Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось Z взять в качестве оси симметрии.
Замечание Бесконечно длинный круглый цилиндр в прямоугольных координатах имеет уравнение
x2 y2 c2 ,
ав цилиндрических — очень простое уравнение
с .
Отсюда и идѐт для данной системы координат имя «цилиндрическая».
Цилиндрическая система координат — только одна из многих трѐхмерных систем координат, существуют законы преобразования координат между цилиндрической системой координат и другими системами
Закон преобразования координат от декартовых к цилиндрическим:
x r cosy r sin
z z
Закон преобразования координат от цилиндрических к декартовым координатам:
r2 x2 y2
arctg( y )
xz z
166
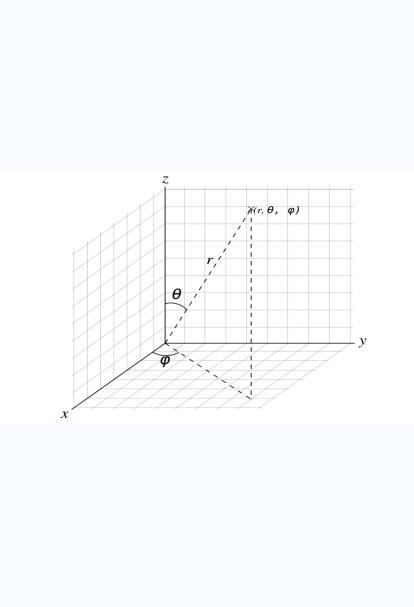
Сферическая система координат
Сферическкую систему координат удобно определять соотносясь с декартовой прямоугольной системой координат.
Определение Сферическими координатами
называют систему координат для отображения геометрических свойств фигуры в трѐх измерениях
посредством задания трѐх координат 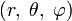 ,
,
где r — расстояние до начала координат, а θ и 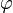 — зенитный и азимутальный угол соответственно.
— зенитный и азимутальный угол соответственно.
Понятия зенит и азимут широко используются в астрономии.
Зенит - это направление вертикального подъѐма над произвольно выбранной точкой (точкой наблюдения),
принадлежащей фундаментальной плоскости.
В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость в которой лежит экватор, или плоскость в которой лежит горизонт, или плоскость эклиптики и т.д., что порождает разные системы небесных координат.
167

Азимут - угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.
Применительно к нашему рисунку сферической системы координат, фундаментальная плоскость, это плоскость xy. Зенит - некая удалѐнная точка, лежащая на оси Z и видимая из начала координат.
Тогда, углы θ и 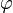 не имеют значения при r = 0, так же как и в первом случае, а
не имеют значения при r = 0, так же как и в первом случае, а 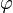 не имеет значения при sin(θ) = 0, так же как и в первом случае, (но уже при
не имеет значения при sin(θ) = 0, так же как и в первом случае, (но уже при 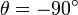 или
или
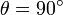 ).
).
Азимут отсчитывается от оси X до проекции радиусвектора r на плоскость xy.
Это объясняет названия углов, как и то, что сферическая система координат может служить обобщением (пусть хотя бы и приближѐнным) множества видов систем небесных координат. Три координаты
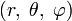 определены как:
определены как:
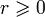 — расстояние от начала координат до
— расстояние от начала координат до
заданной точки P.
 — угол между осью Z и отрезком,
— угол между осью Z и отрезком,
соединяющим начало координат и точку P.
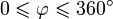 — угол между осью X и проекцией
— угол между осью X и проекцией
отрезка, соединяющего начало координат с точкой P, на плоскость XY (в Америке углы θ и 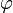 меняются ролями).
меняются ролями).
Угол θ называется зенитным, или полярным, или нормальным, а так же он может быть назван английским словом colatitude, а угол 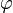 — азимутальным.
— азимутальным.
Углы θ и 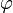 не имеют значения при r = 0, а
не имеют значения при r = 0, а 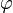 не имеет значения при sin(θ) = 0 (то есть при θ = 0 или
не имеет значения при sin(θ) = 0 (то есть при θ = 0 или 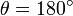 ).
).
Зависимо или независимо от стандарта (ISO 31-11), существует и такое соглашение или конвенция (англ. convention), когда вместо зенитного угла θ, используется угол между проекцией радиус-вектора точки r на плоскость
168

xy и самим радиус-вектором r, и равный 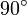 - θ. Он называется углом подъѐма и может быть обозначен той же буквой θ. В этом случае он будет изменяться в пределах
- θ. Он называется углом подъѐма и может быть обозначен той же буквой θ. В этом случае он будет изменяться в пределах
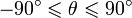 .
.
Переход от сферических координат к декартовым:
От декартовых к сферическим:
От сферических к цилиндрическим:
От цилиндрических к сферическим:
169
Задачи для самостоятельного изучения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1. |
В |
полярной |
системе |
координат |
; r построить точки |
|||||||||||||||||||||||
|
A 0;3 , A |
|
;2 |
, A |
|
;2 |
, A |
|
;2 , A |
|
3 |
;3 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
A |
2 |
; 2 |
, A7 |
|
2 |
;3 |
, A8 |
|
4 |
; 4 , A9 |
|
|
; 3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
2. |
Построить |
линию |
r 2 2cos |
(построение |
|
провести с |
||||||||||||||||||||||
|
помощью таблицы значений r |
|
для 0; |
; |
; |
2 |
; ). |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
3 |
|
||||
3. |
Построить |
|
линии: |
а) r a |
(спираль |
|
|
Архимеда), |
||||||||||||||||||||
|
б) r a 1 cos (кардиоида). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4. |
Построить линии: а) |
r a , б) |
, в) r |
|
|
b |
|
|
. |
|
|
|
||||||||||||||||
|
|
sin |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
5.Написать в полярных координатах уравнение прямой, отсекающей от полярной оси отрезок " a " и перпендикулярной к ней.
6.Написать в полярных координатах уравнение окружности с центром в точке C 0; a и радиусом, равным " a ".
7.Преобразовать к полярным координатам уравнения линий:
а) x2 y2 a2 , |
б) x2 y2 a2 , в) |
y 3 , |
г) y x , |
д) x2 y2 a2 , |
е) x2 y2 2 a2 x2 y2 . |
|
|
8.Преобразовать к декартовым координатам уравнения линии и построить эти линии:
а) r cos a ,б) r 2asin , в) r 2 sin 2 2a2 .
9. Написать канонические уравнения кривых второго порядка:
а) r |
9 |
, б) r |
9 |
, в) r |
3 |
. |
|
|
|
||||
5 4 cos |
4 5 cos |
1 3cos |
170
