Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4613 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Поволжский государственный университет телекоммуникаций и информатики
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Blatov_lek

.pdf
Скачиваний:
76
Добавлен:
10.06.2015
Размер:
3.02 Mб
Скачать
☆

4x z 1 0

3x y z 4 0

б)

2 y 3

0

и

.

x

y 2z 8

0

Ответы к задачам для самостоятельного изучения

1.

а)

x 2

 

 

 

 

 

y

 

 

 

z 3

,

б)

x 2

 

 

y

 

z 3

,

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

2

 

2

1

 

в)

x 2

 

y

 

 

z 3

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

0

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2

 

 

 

 

 

 

y 1

 

 

 

 

 

 

x 2t 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

y 7t 1;

 

 

 

2

 

 

 

 

 

 

7

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

x 8y 5z 3 0

 

 

 

 

 

 

 

 

3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

x 2 y 3z 5 0

 

 

 

 

 

 

 

 

4.

 

x 2

 

 

y 3

 

z 1

;

 

 

 

 

 

 

 

 

 

 

 

 

 

19

 

 

 

 

 

 

 

 

 

 

34

 

 

 

 

 

 

 

 

 

 

 

 

67

 

 

 

 

 

 

 

 

 

 

5.

 

x

 

y

 

 

 

 

z

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

0

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.

cos

 

 

 

 

1

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7.x 4 y 3 z ; 4 3 5

8.x 2 y 3 z 4 ; 2 0 4

 

x 2 0

,

 

x 2

 

y 5

 

z 3

 

9.

а)

 

 

 

б)

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

y 5 0

 

 

 

4

 

6

 

9

 

 

в)

x 2

 

y 5

 

 

z 3

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11

17

 

 

13

 

 

 

 

 

 

 

10. а) да,

б) да.

 

 

 

 

 

 

 

 

 

 

121

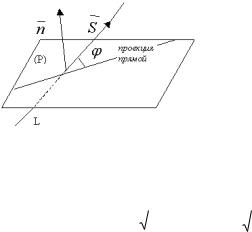
Лекция 10 Взаимное положение прямой и плоскости

Углом между прямой и плоскостью

Пусть плоскость (Р) задана уравнением

Ax By Cz D 0

а прямая L - своими каноническими уравнениями

x x0

 

y y0

 

z z0

m

n

p

 

 

Требуется найти угол между прямой и плоскостью.

Определение Углом между прямой и плоскостью

назовем угол между прямой и ее проекцией на плоскость

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда

угол

 

между

 

 

 

 

 

 

 

 

 

 

 

 

прямой и

плоскостью не

 

 

 

 

 

 

 

 

 

 

 

 

превышает

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пусть

n -

нормальный

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

вектор плоскости, а S -

 

 

 

 

 

 

 

 

 

 

 

 

направляющий

 

вектор

 

 

 

 

 

 

 

 

 

 

 

 

прямой.

 

 

 

 

 

 

 

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Т.к. cos

 

 

 

 

sin , то

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sin

 

n

S

 

 

 

 

Am Bn Cp

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

S

 

A2 B2 C2 m2 n2 p2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Поставим задачу определить координаты точки пересечения прямой и плоскости.

Поскольку точка пересечения одновременно принадлежит и

прямой и плоскости, то ее координаты x, y, z

удовлетворяют

x x

 

y y

0

 

z z

0

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

системе уравнений

m

 

n

 

 

p .

 

 

 

 

Cz D 0

 

 

 

Ax By

 

 

 

Запишем параметрические уравнения прямой

x x0 mt,

y y0 nt,

z z0 pt.

Координаты точки пересечения x, y, z , найденные из уравнений прямой, должны удовлетворять уравнению

плоскости, т.е.

 

 

 

 

 

 

 

 

 

 

A x0 mt B y0 nt C z0 pt D 0.

Отсюда

находим значение параметра t для точки

пересечения

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

Ax0 By0 Cy0 Cz0

 

 

 

Am Bn Cp

 

 

 

и затем с помощью параметрических уравнений прямой

вычисляем координаты точки пересечения x, y, z . Возможны

случаи:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Если

Am Bn Cp n S 0 , то прямая и плоскость

имеют точку пересечения

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Если

Am Bn Cp n S 0 и

Ax0 By0 Cz0 D 0 , то прямая параллельна плоскости, но не принадлежит плоскости.

Если Am Bn Cp n S 0 и

Ax0 By0 Cz0 D 0 , то прямая параллельна плоскости и

точка x0 , y0 , z0 прямой удовлетворяет уравнению плоскости, т.е. прямая принадлежит плоскости.

Условие параллельности прямой и плоскости

векторы a l, m, n и

N A, B,C должны быть

перпендикулярны

Al Bm Cn 0

-условие параллельности прямой и плоскости.

123

Пример Составить уравнение плоскости, проходящей через прямую

3x 2 y 5z 6 0x 4 y 3z 4 0

и параллельно прямой

x 1

 

y 5

 

z 1

.

 

 

 

3

2

 

3

Решение

Составим уравнение пучка плоскостей

3x 2y 5z 6 x 4y 3z 4 0

или

3 x 2 4 y 5 3 z 6 4 0

используем условие параллельности прямой и плоскости

Al Bm Cn 0

имеем

3 3 2 2 4 3 5 3 0

1,имеем

4x 6y 8z 10 0 .

Условие перпендикулярности прямой и плоскости

Векторы a l, m, n и N A, B,C должны быть параллельны

Al mB Cn

-условие перпендикулярности прямой и плоскости.

Пример Написать каноническое уравнение прямой,

проходящей

через точку

K 3; 7;7

перпендикулярно

плоскости,

содержащей

точки

L 6;2; 2 , M 1; 5;5 ,

N 2;3;1 .

 

 

 

 

Решение

За вектор нормали плоскости, проходящей через точки L, M , N, можно взять вектор, коллинеарный вектору

LM LN :

124

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

LM 7i 7j 3k,

 

LM 8i j 3k,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

j

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

18i 45j 63k 9 2i 5j 7k

 

 

LM LN

7

7

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8

1

 

3

 

 

 

 

 

 

 

 

 

 

 

 

n 2i 5j 7k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вектор нормали

к

 

 

плоскости

является направляющим

вектором

 

 

 

прямой

 

S ,

проходящей

через

току

K

перпендикулярно плоскости

L M N

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S :

x 3

 

y 7

 

z 7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

-

 

 

 

 

 

 

каноническое

 

уравнение

 

прямой.

Ответ

 

x 3

 

y 7

 

z 7

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример Написать общее уравнение плоскости,

проходящей

через

 

 

 

точку

L 3; 2;9

и

прямую

 

x 5

 

y 6

 

 

z 9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

4

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M 5;6; 9

 

 

По условию прямая проходит через

точку

в

направлении вектора

 

 

s 4i 4 j k . Чтобы

найти вектор

нормали

 

 

 

 

 

плоскости,

необходимо

 

найти

вектор

 

 

 

 

 

 

 

 

 

 

LM 8i 8j 18k , а затем векторное произведение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

j

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

80i 64j 64k 16 5i 4j 4k

 

 

s LM

4

 

 

4

 

 

 

 

 

 

 

 

 

8

 

 

8

 

 

18

 

 

 

 

 

 

 

 

 

 

 

 

Следовательно,

n 5i 4 j 4k

-

 

вектор

нормали

плоскости.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5 x 3 4 y 2 4 z 9 0,

5x 4y 4z 0

-

общее уравнение плоскости.

Ответ 5x 4y 4z 13 0 .

125

Пример Найти расстояние между прямыми:

 

x 5

 

y 5

 

z 8

,

x 4

 

y 6

 

z 7

 

 

 

 

5

 

 

5

7

 

2

 

 

6

 

 

1

 

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

Расстояние

p между

прямыми

равно

длине вектора,

соединяющего две точки, принадлежащие разным прямым, который имеет среди всех возможных векторов наименьшую длину.

Если найти плоскость P ,проходящую через одну прямую параллельно второй, то очевидно, что расстояние p между

прямыми будет равно расстоянию между этой плоскостью и произвольной точкой второй прямой. Найдем эту плоскость.

С этой целью ищем вектор нормали плоскости P :

 

i

j

k

 

 

7

2

5

5i 5j 5k, n i j k.

 

6

1

5

 

x 5 y 5 z 8 0, P : x y z 8 0

 

 

 

 

-общее уравнение плоскости.

Находим нормальное уравнение плоскости P :

 

x

 

 

y

 

 

z

 

 

 

8

 

 

 

 

 

4

 

 

6

 

 

7

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

0, p

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

3

 

 

3

3

 

 

3

 

 

3

 

 

 

3

 

 

 

 

 

 

 

3

 

 

 

 

 

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример Найти расстояние от точки

M 7; 1;8

до

 

 

 

 

прямой

 

x 5

 

y 4

 

z 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Найдем

 

 

плоскость

P ,

проходящую

через

точку

M

перпендикулярно заданной прямой L .

2 x 7 3 y 1 z 8 0, P : 2x 3y z 19 0

Найдем точку пересечения N прямой L и плоскости P . Для этого следует решить систему линейных уравнений:

126

x 5 2t

 

 

 

y 4 3

 

 

 

z 1 t

 

 

0

2x 3y z 19

 

x 2t 5

 

y 3t 4

z 1 t

 

2 2t 5 3 3t 4 1 t 19 0

t

20

 

 

5

 

32

 

27

 

 

, N

 

,

 

,

 

.

 

 

 

 

 

7

 

 

7

 

7

 

7

 

Расстояние p от точки M до прямой L равно MN , т.к.

 

44

 

39

 

29

 

 

 

4298

 

 

i

j

k, то p

 

 

MN

MN

7

7

7

7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: p

4298

7

Контрольные вопросы по теме «Прямая и плоскость»

1.Как вычислить угол между прямой и плоскостью?

2.Условия параллельности и перпендикулярности прямой и плоскости.

3.Как выяснить, что прямая и плоскость имеют точку пересечения, прямая принадлежит плоскости, прямая параллельна плоскости и не принадлежит ей?

Задачи для самостоятельного

изучения

1. Доказать, что прямая

x 3t 2, y 4t 1, z 4t 5

параллельна плоскости 4x 3y 6z 5 0 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5x 3y 2z 5 0

 

2.

Доказать, что прямая

 

лежит в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2x y z 1 0

 

3.

плоскости 4x 3y 7z 7 0 .

 

4.

Найти

точку

 

пересечения прямой и

плоскости:

 

а)

x 1

 

y 1

 

z

,

2x 3y z 1 0 ;

 

 

 

 

 

2

 

 

 

 

 

 

 

1

 

 

 

 

6

 

 

 

 

 

5.

б)

x 3

 

 

y 2

 

z 1

, x 2 y z 15 0 ;

 

 

 

1

 

 

 

 

 

3

 

 

 

 

 

 

 

 

5

 

 

 

 

6.

в)

x 2

 

 

y 1

 

 

z 3

, x 2 y 2z 6 0 .

2

 

 

 

 

 

 

 

 

3

 

 

2

 

 

 

 

127

7.Составить уравнение плоскости, проходящей через точку M (1; 2;1) перпендикулярно к прямой

x 2 y z 3 0

8. .

x y z 2 0

9.При каких значениях A и D прямая

10.x 4t 2, y 4t 1, z t 3 лежит в плоскости

11.Ax 2y 4z D 0 ?

12.Найти проекцию точки M (3; 1;3) на прямую

13.x 3t, y 5t 7, z 2t 2 .

14.Найти проекцию точки M (5;2; 1) на плоскость

15.2x y 3z 23 0 .

16.Найти точку Q, симметричную точке P(1;3; 4)

17.относительно плоскости 3x y 2z 0 .

18.Найти уравнение плоскости, которая проходит через

19.

точку M (3;1; 2) и через прямую

x 4

 

y 3

 

z

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

2

1

 

20.

Проверить, что прямые

x 3

 

y 1

 

z 2

 

и

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

2

 

 

 

 

4

 

 

 

 

 

21.

 

x 8

 

 

y 1

 

 

 

z 6

 

 

пересекаются, и написать

3

1

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22.

уравнение плоскости, проходящей через них.

 

 

 

 

23.

Найти

расстояние

 

между

 

 

двумя

прямыми:

 

 

x 2

 

y 1

 

z

и

x 7

 

 

y 1

 

z 3

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

4

 

2

 

 

 

3

 

 

4

 

2

 

 

 

 

 

 

 

 

Ответы к задачам для самостоятельного решения

 

 

 

 

1.

а) 2; 3;6 ,

 

 

 

 

 

 

 

 

 

 

4.

(3; - 2; 4);

 

 

 

 

б)

прямая

параллельна

 

 

 

 

5.

(1; 4; - 7);

 

 

 

 

 

 

 

 

6.

(- 5; 1; 0 );

 

 

 

плоскости,

в)

прямая

 

 

 

 

 

 

 

 

 

 

 

7.

x 9y 22z 59 0

лежит в плоскости;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

x 2y 3z 0 ;

 

 

 

 

8.

8x 22y z 48 0

3.

A 3, D 23 ;

 

 

 

 

9.

3.

 

 

 

 

 

 

 

 

 

 

128

Лекция 11 Кривые второго порядка

В этом параграфе будем рассматривать алгебраические линии второго порядка. Самое общее уравнение алгебраической линии второго порядка имеет вид

a11x2 2a12xy a22 y2 2a1x 2a2 y a0 0

Мы подробно рассмотрим кривые 2-го порядка: окружность, эллипс, гипербола, парабола. Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса».

Аполлоний Пергский( 262г. до н. э.) -великий геометр античности, живший в III веке до н. э. Аполлоний прославился в первую очередь выдающейся работой «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Он ввѐл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата.

Определение Геометрическое место точек, отношение расстояний которых от фиксированной точки (фокуса) к расстоянию до фиксированной прямой (директрисы) постоянно и равно числу e (эксцентриситету), является кривой второго порядка.

Если e < 1 то это эллипс, если e = 1 то это парабола, если e > 1

то это гипербола.

Окружность

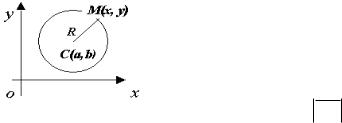
Определение Окружность - геометрическое место точек, равноудаленных от точки, называемой центром окружности.

Пусть центр окружности находится в точке C a, b .

Так как окружность есть множество

точек

M x, y , находящихся на

расстоянии R (радиус окружности) от центра C a, b , то CM R , т.е

129

x a 2 y b 2 R2

уравнение окружности с центром в точке C a,b и

радиусом R .

Если центр окружности находится в начале координат, то ее уравнение примет вид:

x2 y2 R2

Пример Найти координаты центра и радиус окружности x2 y2 6x 10y 15 0 .

Решение В данном уравнении выделим полные квадраты, прибавляя и вычитая соответствующие числа.

Получаем

x2 6x 9 y2 10 y 25 9 25 15 0,

x 3 2 y 5 2 49

Отсюда, находим a 3,b 5, R 7 .

Эллипс

Определение Эллипс - геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

130

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности