Blatov_lek

9. Найти A E и E A ( E - единичная матрица) и сравнить результаты.

Ответы к задачам для самостоятельного изучения

21

Лекция 2 Теория определителей

С точки зрения истории, феномен определителя стал изучаться ранее, чем сами матрицы. Первоначально, определитель был представлен как собственно система линейных уравнений. Определитель «определял» имеет система одно или несколько возможных решений.

Впервые определители начали использовать в китайских учебниках по математике. В Европе Крамер (1750) добавил к уже проведенным исследованиям в этой области, так называемое положение о системах уравнений. И только лишь в 1771г. Вандермонд впервые представил определители в виде независимых функций, а в 1772г. Лаплас сделал популярным среди математиков общий метод разложения определителя на дополнительные миноры. Лагранж — первый, кто начал изучение определителей в рамках теории исключения. Гаусс в 1801г начал использовать феномен определителя в теории чисел. Он ввел в обиход термин «детерминант» (Лаплас называл его «результантом»).

Теория определителей возникла при решении и исследовании систем линейных алгебраических уравнений со многими неизвестными.

Исследование системы двух линейных уравнений

Теория определителей возникла при решении и исследовании систем линейных алгебраических уравнений со многими неизвестными.

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

a1 x b1 y c1a2 x b2 y c2

Найдем решение, умножая первое уравнение на b2 , а второе на b1 , получим

xc1b2 c2b1 a1b2 a2b1

22

а, умножая первое уравнение на a2 , а второе на a1 , получим

ya1c2 a2c1 a1b2 a2b1

Таким образом, если a1b2 a2 b1 0 , то система имеет единственное решение.

определителем 2-го порядка

.

Заметим, что числители в формулах решения системы уравнений можно преобразовать

 Замечание Вычислить определитель 2-го порядка означает найти разность из произведения элементов, стоящих на главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) и произведения элементов, находящихся на побочной, диагонали.

23

Крамер Габриэль (1704-1752) швейцарский математик, родился в Женеве, основные работы относятся к высшей алгебре и аналитической геометрии, установил правила решения систем n линейных уравнений с n неизвестными, заложил основы теории определителей.

Правило Крамера

Если определитель системы не равен нулю, то решение системы единственно.

Каждое из неизвестных равно частному двух определителей с общим знаменателем, равным определителю системы, числителями служат определители, получаемые из определителя системы заменой столбца коэффициентов, стоящих при определяемом неизвестном, столбцом свободных членов уравнений системы.

 Замечание Правило Крамера остается справедливым и для линейных систем n уравнений с n неизвестными при любом n .

Пример Решить систему уравнений

 Определение Система, не имеющая ни одного решения, называется несовместной, система, обладающая хотя бы одним решением, называется совместной.

Пусть определитель системы

a1x b1 y c1a2 x b2 y c2

24

но одновременно a2 a1, тогда

a2 x b2 y a1 x b1 y

Вывод: если c2 c1 , то второе уравнение следствие

первого, поэтому система сводится к одному уравнению, так как в этом уравнении два неизвестных, то система – неопределенна и имеет бесчисленное множество решений,

если c2 c1, то уравнения противоречивы, и система не имеет решений.

Или если определитель системы A 0 , то система имеет

единственное решение, находящееся по формулам Крамера, или

совместна, или определена.

имеет, она противоречива или несовместна.

Если А 0 , и все определители равны нулю, а хотя бы

один из коэффициентов при неизвестных не равен нулю, то система имеет бесконечное множество решений или неопределена.

2x 3y 5

Пример Решить систему уравнений

4x 6 y 7

Ответ: решений нет

3x 4 y 5

Пример Решить систему уравнений

6x 8y 10

25

бесчисленное множество решений.

Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы.

Это число называется определителем

 Определение Определитель третьего порядка - число,

определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

 Замечание Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников (правило Саррюса).

Оно заключается в следующем:

26

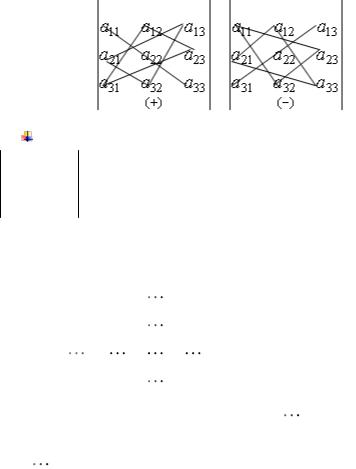
элементы, произведения которых входят в определитель со знаком «+», располагаются так: образуя два треугольника, симметричных относительно главной диагонали.

Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали.

1 1 1 4 15 4 6 40 1 58

Определение Определитель n-го порядка называется

которых соответствует одному из n! упорядоченных множеств k1k2 kn , полученных r - попарными перестановками

элементов из множества 1,2, n .

Размерность матрицы, для которой ищется определитель, задает его порядок.

27

 Замечание Получить формулы, аналогичные формулам для систем n уравнений с n неизвестными затруднительно, так как число слагаемых, из которых составляется определитель n - го порядка очень быстро растет с увеличением порядка ( определитель n -го порядка содержит n!слагаемых ).

Замечание Число сомножителей в каждом произведении равно порядку матрицы.

 Определение Матрица невырожденная - квадратная матрица имеющая определитель, отличный от нуля ( 0 ), в противном случае - матрица вырожденная или особая.

Замечание Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Замечание Определитель бывает только у квадратных матриц.

Замечание Иногда вместо термина определитель используют термин детерминант.

Замечание Если все элементы матрицы n -го порядка, расположенные выше или ниже главной диагонали равны нулю, то определитель такой матрицы равен произведению элементов, лежащих на главной диагонали.

 Определение Определитель вида

28

называется определителем Вандермонда порядка n

(степенной определитель).

Вандермонд Александр (1735-1796) – французский математик, участник Великой французской революции. Родился в Париже. Предложив специальный символ определителя дал новый толчок развитию учению об определителях, впервые логично изложил теорию детерминантов

Его труды были забыты во Франции и обратил внимание Л.Кронекер (немецкий математик уже через 100 лет, он также занимался системами линейных уравнений).

 Определение Минор порядка k матрицы A -

определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.

Пусть дана матрица А n -го порядка. Вычеркнем в ней i -ю

строчку и k -й столбец и сдвинем, не нарушая порядка, оставшиеся элементы. Определитель полученной матрицы

n 1 - го порядка называется минором элемента i -й строчки

иk -го столбца матрицы А и обозначается Mik .

Пример. Дан определитель

 Замечание Определитель всякой матрицы есть число, то миноры элементов матрицы также являются числами. Для

матрицы n -го порядка имеем n2 различным образом составленных миноров (для каждого элемента свой минор).

 Определение Минор Mik взятый со знаком 1 i k

называется алгебраическим дополнением этого элемента.

Обозначается Aik .

Aik 1 i k Mik

29

 Замечание Каждый элемент матрицы является ее

 Замечание Для элементов, расположенных на главной диагонали, алгебраическое дополнение совпадает с минором

Aii 1 2i Mii Mii

 Замечание Минор Mij элемента aij берется со своим

знаком, если сумма его индексов четна, и с обратным, если сумма нечетна.

Свойства определителей

1. При транспонировании определитель матрицы не меняется («равноправие» строк и столбцов определителя)

detA detAT

2.При перемене местами двух строчек (или столбцов) определитель меняет знак.

3.Определитель, имеющий нулевую строку, равен 0.

30