
Blatov_lek
.pdf
Выберем прямоугольную систему декартовых координат так, чтобы ось абсцисс проходила через оба фокуса F1 и F2 , начало координат находится в середине отрезка F1F2 .
Если обозначить расстояние между фокусами F1 и F2 через 2c , тогда координаты фокусов будут соответственно c;0 и
c;0 .
Пусть M x, y - текущая точка эллипса.
Обозначим сумму расстояний F1M и F2 M через 2a ( a c по правилу треугольника), т.е.
F1M F2 M 2a ,
или

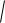 x c 2 y2
x c 2 y2 
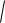 x c 2 y2 2a
x c 2 y2 2a
- уравнение эллипса.
Приведем его к более простой для исследований форме:

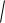 x c 2 y2 2a
x c 2 y2 2a 
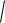 x c 2 y2 ,
x c 2 y2 ,
x2 2cx c2 y2 4a2 4a
 x c 2 y2 x2 2cx c2 y2 , a2 cx a
x c 2 y2 x2 2cx c2 y2 , a2 cx a
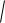 x c 2 y2 ,
x c 2 y2 ,
a4 2a2cx c2 x2 a2 x2 2a2cx a2c2 a2 y2 ,a2 c2 x2 a2 y2 a2 a2 c2 .
Поскольку a c , то можно обозначить |
a2 c2 |
b2 |
|
тогда получаем |
b2 x2 a2 y2 |
a2b2 |
|
Окончательно получим (при выбранной системе координат) уравнение
x2 |
|
y2 |
1 |
|
a2 |
b2 |
|||
|
|
Уравнение называют каноническим уравнением эллипса и c 
 a2 b2 .
a2 b2 .
131
Замечание Так как в процессе преобразований дважды возводились в квадрат обе части уравнения, то необходимо проверить, не получены ли "лишние" точки.
Для этого нужно показать, что если координаты произвольной |
|||||||
точки |
|
M0 x0 , y0 |
удовлетворяют |
уравнению, |
то |
||
|
|
|
|
2a . |
|
|
|
|
F1M0 |
F2 M0 |
|
|
|
||
|
|
Замечание Оси координат Ox и |
Oy являются осями |
||||
симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса.
Рассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать уравнение в виде:
y b |
1 |
x2 |
|
|
a2 |
|
|||
|
|
|
||
|
|
|
Отсюда видно, что если x 0 , то |
|
|
|
|
y b и, далее, с ростом x |
значения |
|
|
|
y |
|
|
|
|
убывают. Когда x a , то y 0 . |
|
|
|
|
Числа a и b называют полуосями |
|
|
|
|
эллипса |
|
|
|
|
Учитывая симметрию |
эллипса |
|
|
|
относительно осей координат, можем |
|
построить полный эллипс. |
|
|||
132
Если изменяется величина с, то меняется форма эллипса, а
именно: |
если |
c a, |
то |
b a и |
при c 0 |
эллипс |
||||
становится окружностью с уравнением |
|
|
||||||||
|
|
|
x2 y2 a2 |
|
|
|||||
Таким образом, окружность есть частный случай эллипса, |
||||||||||
когда полуоси эллипса равны между собой. |
|
|||||||||
|
|
|
|
|
|
|
||||
Если же c a , то b |
|
a2 |
c2 0 , т.е. эллипс сжимается |
|||||||
вдоль |
оси Oy . |
Величина |
|
c |
может |
служить |
числовой |
|||
|
|
|||||||||
|
|
|
|
|
|
a |
|
|
||
характеристикой сжатия эллипса.
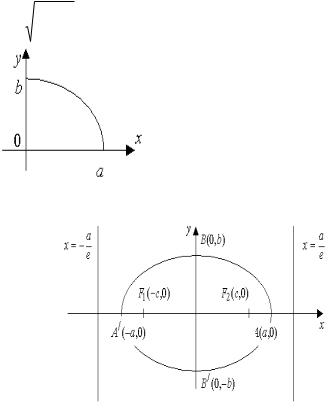
Определение Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси.
ac
Форма эллипса зависит от b
a
Замечание Так как c a , то 1 у эллипса.
с2 a2 b2
|
b |
2 |
b |
|
|
|
||
|
|
|
|
2 |
||||
|
1 |
|
|
или |
|
|
1 |
|
|
|
|
||||||
|
a |
|
a |
|
|
|
||
чем больше эксцентриситет, тем более эллипс вытянут, в
случае окружности 0 .
Замечание |
x a cos t, y bsin t - параметрическое |
уравнение эллипса.
Определение Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно
a
центра на расстоянии от него называют директрисами
эллипса.
x a
133

Точки пересечения эллипса с осями симметрии
A, B, A B называют вершинами эллипса.
r1 |
F1P |
a ex, |
r2 |
F2 P |
a ex, - |
левый и правый |
|||||||||||||||||
фокальные радиусы точки P(x, y) , |
|
|
|||||||||||||||||||||
|
|
|
|
|
a |
x, |
|
|
|
|
|
|
|
|
|
a |
|
|
|||||
q |
|
N P |
|
q |
2 |
|
N |
2 |
P |
|
x, - |
расстояния от |
|||||||||||
|
|
|
|
|
|||||||||||||||||||
1 |
|
1 |
|
|
|
e |
|
|
|
|
|
|
|
|
e |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точки |
P до левой и правой директрисы. |
|
|||||||||||||||||||||
Свойства эллипса
1.Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса).
2.Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков,
образованных пересечением эллипса с главными осями, равны 2a и 2b ( 2a 2b ), то главная ось, проходящая через фокусы, называется большой осью эллипса, а
вторая главная ось – малой осью.
3. Весь эллипс содержится внутри прямоугольника
xa, y b .
4.Эксцентриситет эллипса e 1.
5.Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно ae ,
а e 1, следовательно, |
a |
a , а весь эллипс лежит в |
|
e |
|||
|
|
прямоугольнике x a, y b )
6.Отношение расстояния ri от точки эллипса до фокуса Fi
красстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.
134
Доказательство
Расстояния от точки M (x, y) до фокусов эллипса можно представить так: r1 a ac x a ex, r2 a ac x a ex
Составим уравнения директрис:
|
|
x |
a |
|
0 (D1), |
|
x |
a |
|
|
0 (D2). |
|
|
|
|||||||||||||||||
|
e |
e |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
d |
a ex |
, d |
|
|
a ex |
Отсюда r d |
|
e , что |
и |
|||||||||||||||||||||
|
|
2 |
|
|
|
i |
|||||||||||||||||||||||||
|
1 |
|
|
|
e |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример Определить вид и расположение кривой второго |
|||||||||||||||||||||||||||||||
порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2y2 2x 3y 0 . |
|
|
|
||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дополним |
члены, содержащие |
|
x |
|
и y соответственно, |
до |
|||||||||||||||||||||||||
полных квадратов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x 1 2 2 y |
3 2 |
1 |
9 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
8 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||
Отсюда получаем |
x 1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||
17 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
8 |
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, кривая, заданная исходным уравнением, |
|||||||||||||||||||||||||||||||
представляет |
|
|
|
|
|
|
|
|
собой |
|
|
|
|
|
|
|
|
|
|
|
|
эллипс |
|
|
с |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
полуосями a |
|
17 |
|
|
1.46 |
и |
|
|
b |
|
|
17 |
|
|
1.03 . |
|
|
|
|||||||||||||
8 |
|
|
|
|
|
16 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Центр эллипса находится в точке O(1, 34) .
Замечание Из канонического уравнения эллипса легко заключить, что эллипс можно задать в параметрической форме.
x a cos t, |
y b sin t , где a , b –большая и малая полуоси, |
t —угол. |
|
135
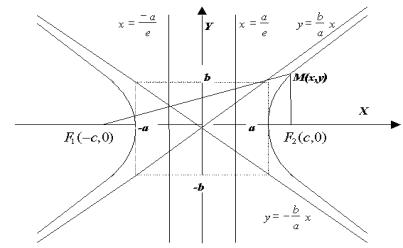
Гипербола
Термин «гипербола» (греч. ὑπερβολή — избыток) был введѐн Аполлонием Пергским, поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
Определение Гипербола - геометрическое место точек, абсолютное значение разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).
Расстояние между фокусами F1 и F2 обозначим 2c . Систему координат выберем так же, как при выводе уравнения эллипса.
Пусть точка M - произвольная точка гиперболы. Отрезки F1M и F2 M - фокальные радиусы точки M . Таким образом, для любой точки M
F1M F2M 2a
Расстояние F1F2 2c . Координаты F1 c,0 , F2 c,0
Пусть точка M x, y - произвольная точка гиперболы.
Отрезки r1 F1M и r2 F2 M - фокальные радиусы точки M .
136
Применяя формулу расстояния между двумя точками, имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|||
r1 |
x c 2 |
y2 , r2 |
|
x c 2 y2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
F1M F2 M 2a |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2a , |
|
|||||||||||
|
x c 2 y2 |
x c 2 y2 |
|
|||||||||||||||||||
Преобразуем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2a |
|
|
|
|
|
|
|
||||||||||||
|
x c 2 y2 |
x c 2 y2 |
|
|||||||||||||||||||
Возведем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
||
квадрат x c 2 y2 |
4a2 4a |
|
|
|
x c 2 y2 , |
|||||||||||||||||
x c 2 y2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
cx a2 a |
|
x c 2 |
y2 |
,возведем |
в |
|||||||||||||||||
квадрат c2 x2 2a2cx a4 |
a2 |
2a2cx a2c2 |
a2 y2 , |
|||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
c2 a2 x2 a2 y2 a2 c2 a2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
Обозначим b |
c2 a2 |
, так как c a , то b - вещественная |
||||||||||||||||||||
величина. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, имеем |
|
|
b2 x2 a2 y2 a2b2 |
|
||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
||||||||
каноническое уравнение гиперболы. |
|
|||||||||||||||||||||
Гипербола – кривая 2 –го порядка |
|
|||||||||||||||||||||
Число |
a называют действительной полуосью гиперболы, |
|||||||||||||||||||||
число b - мнимой полуосью.
Отметим, что согласно уравнению гипербола симметрична относительно осей координат и, следовательно, относительно начала координат. Т.к. из канонического уравнения гиперболы
следует, что |
|
|
|
||
|
b |
|
|
|
|
y |
|
x2 a2 , |
|||
a |
|||||
|
|
|
|
||
то нет точек кривой в полосе a x a .
Кривая состоит из двух отдельных частей - ветвей гиперболы, лежащих в областях x a и x a .
137

Можно показать, что при x ветви гиперболы неограниченно приближаются к прямым y ba x , не пересекая
этих прямых.
Эти две прямые называются асимптотами гиперболы.
Определение Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами.
ac
Замечание Так как c a , то 1 у гиперболы.
с2 a2 b2 ,
|
b 2 |
b |
|
|
|||
|
|
2 1 |
|||||
|
1 |
|
|
или |
|
||
|
|
||||||
|
a |
|
a |
|
|
||
|
|
|
|
|
|
|
|
Эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а значит и форму самой гиперболы.
Чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник
Точки пересечения гиперболы с действительной осью называются вершинами гиперболы.
Определение Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает и расположенные
симметрично относительно центра на расстоянии |
a |
от него |
||||
|
||||||
|
|
|
|
|
||
называют директрисами гиперболы. |
|
|
||||
|
x |
a |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||
Директрисы гиперболы параллельны оси Oy и пересекают |
||||||
ось Ox между вершинами гиперболы. |
|
|
||||
|
Замечание Если a b , гипербола называется |
|
|
|||
равнобочной.
Замечание В системе координат, оси которой совпадают
сасимптотами - равнобочные гиперболы. Она имеет уравнение
138
y |
k |
. |
|
|
Асимптоты |
равнобочной |
гиперболы |
взаимно |
|||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
перпендикулярны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Определение Сопряженные гиперболы - |
x2 |
|
y2 |
1 . |
||||||||||||||||||||||||
|
b2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|||
Сопряженные гиперболы имеют общие асимптоты. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
r1 |
F1P a ex, |
r2 |
F2 P |
a ex |
|
- левый |
и |
правый |
|||||||||||||||||||||
фокальные радиусы точки P x, y , |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
a |
x, |
q2 |
|
|
|
|
|
|
a |
x |
|
|||||||||||||
q1 |
|
|
|
|
|
- расстояния от |
|||||||||||||||||||||||
N1P |
N2 P |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
точки |
|
P до левой и правой директрисы. |
|
|
|||||||||||||||||||||||||
Свойства гиперболы
1.Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ox для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Oy ). По обе стороны от нее
расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.
2.Ветви гиперболы имеют две асимптоты, определяемые уравнениями
|
y |
b |
|
x и |
y |
b |
x . |
|
|||
|
|
|
|
||||||||
|
|
|
a |
|
|
|
|
|
a |
|
|
3.Наряду с гиперболой можно рассмотреть так |
|||||||||||
называемую |
сопряженную |
гиперболу, |
определяемую |
||||||||
каноническим уравнением |
|
|
|
|
|
|
|
|
|||
|
|
x2 |
|
|
y2 |
|
1 |
, |
|
||
|
|
a2 |
|
b2 |
|
||||||
|
|
|
|
|
|
|
|
||||
для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.
139
4.Эксцентриситет гиперболы e 1.
5.Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу
директрисы равно эксцентриситету гиперболы. Доказательство можно провести так же, как и для эллипса.
 Пример Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы
Пример Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы
9x2 16y2 144 .
Решение
Приведем данное уравнение к каноническому виду
(разделив его на 144): x2 y2 1.
16 9
Отсюда следует, что a2 16, b2 |
9 . |
|
|
|
|
|
|||||||||
Следовательно, a 4 |
|
-действительная полуось, |
b 3 - |
||||||||||||
мнимая полуось. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда c |
16 9 5 |
5,0 , |
F2 5,0 . |
||||||||||||
Значит, фокусы имеют координаты F1 |
|||||||||||||||
Находим эксцентриситет |
c |
|
5 |
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a |
4 |
|
|
|
|
|
|
||
Уравнения |
асимптот |
имеют вид y |
3 |
x , а |
уравнения |
||||||||||
4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
директрис x 165 .
Парабола
140
