
- •Федеральное агентство связи
- •Оглавление
- •Общее представление о предмете электротехника
- •Основные понятия в теоретической электротехнике
- •Понятия об электрической цепи и схеме
- •Расчет цепей на постоянном токе
- •Законы Кирхгофа
- •Переменные токи и напряжения Основные понятия и параметры
- •Оценка переменного тока и напряжения
- •Понятия о комплексных и полных сопротивлениях электрической цепи
- •Гармонический ток в пассивных элементах электрической цепи
- •3 Емкость
- •Анализ последовательной rlc-цепи при гармоническом воздействии
- •Параллельные rlc - цепи
- •Принцип дуальности в электрических цепях
- •Принцип и метод наложения в теории цепей.
- •Теоремы об эквивалентных источниках или генераторах (Теорема об автономном двухполюснике)
- •Теорема обратимости или взаимности
- •Примеры
- •Колебательные контуры и резонансы в электрических цепях
- •Последовательный колебательный контур
- •Частотные характеристики последовательного контура
- •Влияние внешнего сопротивления на избирательность контура
- •Параллельный колебательный контур (простой)
- •1. Идеализированный контур
- •Реальный параллельный контур
- •Частотные зависимости параллельного контура
- •Влияние внешних сопротивлений на избирательность контура (Добротность, полоса пропускания, коэффициент подавления)
- •Сложные параллельные контуры
- •Мощность в цепи переменного тока
- •Расчет мощности в комплексной форме
- •Баланс мощности в цепях переменного тока
- •Физический смысл баланса мощности
- •Определение условия максимума активной мощности при передаче энергии от источника в нагрузку
- •Электрические цепи с взаимно индуктивными связями и методы их расчета Основные понятия о взаимной индукции
- •Последовательное и параллельное соединения индуктивно связанных элементов
- •1. Последовательное соединение
- •2. Параллельное соединение
- •Электрический трансформатор
- •2.Уравнения и схемы замещения реального трансформатора (двухобмоточного, без ферромагнитного сердечника)
- •Входное сопротивление реального трансформатора
- •Переходные процессы в электрических цепях Основные понятия о переходных процессах
- •Законы коммутации
- •Начальные и конечные условия
- •Схемы замещения элементов в различные моменты времени
- •IL (0_) l пост
- •Классический метод расчета переходных процессов
- •Анализ переходных процессов в rlc цепях классическим методом Последовательные и параллельные rl и rc цепи
- •Переходные процессы в rlc цепях Последовательная rlc цепь Подключение источника постоянного напряжении
- •Отключение источника в последовательной rlc-цепи
- •Расчет переходных процессов в сложных цепях
- •Операторный метод расчета переходных процессов Преобразования Лапласса
- •Операторные схемы замещения реактивных элементов
- •Нахождение функции времени в операторном методе
- •Операторные передаточные функции
- •Методы расчета передаточных функций
- •Временные характеристики электрических цепей
- •Методики расчета временных характеристик
- •Пример нахождения временных характеристик
- •Расчет откликов в электрической цепи на кусочно-непрерывное воздействие. (Интеграллы Дюамеля и наложения)
- •Определение отклика на прямоугольный импульс.
- •Дифференцирующие и интегрирующие цепи Общие понятия
- •Дифференцирующие цепи
- •Интегрирующие цепи
- •Спектральный метод расчета в электрических цепях Понятие о спектре периодического сигнала
- •Спектральный анализ и синтез на основе рядов Фурье
- •Графическое временное и частотное изображения спектра периодического сигнала
- •Спектр последовательности прямоугольных импульсов
- •Понятие о расчете цепей при периодических сигналах
- •Понятие о спектре непериодического сигнала
- •Спектры некоторых типовых сигналов
- •Понятие об энергетическом спектре одиночных сигналов. Ширина спектра
- •Условия безыскаженной передачи электрических сигналов
- •Нелинейные электрические цепи Основные понятия о нелинейных цепях
- •Расчет простейших нелинейных резистивных цепей
- •Аппроксимация характеристик нелинейных элементов
- •Определение реакции нелинейного элемента на гармоническое воздействие
- •Анализ спектра реакции в нелинейном элементе
- •Линейные цепи с распределенными параметрами. Длинные линии.
- •Уравнения однородной линии в стационарном режиме
- •Бесконечно длинная однородная линия. Согласованный режим работы
- •Линия без искажений
- •Уравнения линии конечной длины
- •Уравнения длинной линии как четырехполюсника
- •Линия без потерь
- •Стоячие волны в длинных линиях
- •Волновое сопротивление длинной линии.
- •Теория четырехполюсников Основные понятия и классификация четырехполюсников
- •Основные характеристики четырехполюсников
- •Системы параметров. Матричные параметры чп
- •Сложные четырехполюсники. Виды соединений чп
- •Рабочие параметры чп
- •Характеристические параметры четырехполюсников
- •Каскадное согласованное включение четырехполюсников
- •Рабочая мера передачи
- •Теория электрических фильтров Общие понятия
- •Классификация частотно – избирательных электрических фильтров
- •Лестничные реактивные фильтры
- •Реактивные фильтры типа к
- •Теорема о реактивных фильтрах типа к
- •Фнч типа к (полузвено)
- •Фнч типа к (полузвено)
- •Фвч типа «к» (полузвено)
- •Полосовые фильтры типа «к»
- •Режекторный фильтр типа «к»
- •Достоинства и недостатки фильтров типа k
- •Искажения сигнала в эц
- •Корректирующие цепи (корректоры). Общие положения.
- •Принцип корректирования амплитудно-частотных искажений (ачи)
- •Стандартные схемы амплитудных корректоров
- •Фазовые корректоры
- •Электрические машины постоянного тока Устройство электрической машины постоянного тока
- •Принцип действия машины постоянного тока
- •Работа электрической машины постоянного тока в режиме генератора
- •Генераторы с независимым возбуждением. Характеристики генераторов
- •Генераторы с самовозбуждением. Принцип самовозбуждения генератора с параллельным возбуждением
- •Работа электрической машины постоянного тока в режиме двигателя. Основные уравнения
- •Механические характеристики электродвигателей постоянного тока
- •Электрические машины переменного тока Вращающееся магнитное поле
- •Информационные электрические машины Сельсины
- •Поворотные трансформаторы. Индуктосины. Редуктосины
- •Тахогенераторы
- •Шаговые электродвигатели
Уравнения линии конечной длины
П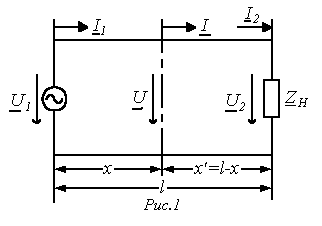 остоянные
остоянные![]() и
и![]() в
полученных в предыдущей лекции формулах
в
полученных в предыдущей лекции формулах
|
|
(5) |
|
|
(6) |
определяются на основании граничных условий.
Пусть для линии
длиной l(см. рис. 1) заданы напряжение![]() и
ток
и
ток![]() в
начале линии, т.е. приx=0.
в
начале линии, т.е. приx=0.
Тогда из (5) и (6) получаем
![]()
![]()
откуда
![]()
![]()
Подставив найденные
выражения
![]() и
и![]() в
(5) и (6), получим
в
(5) и (6), получим
|
|
(7) |
|
|
(8) |
Уравнения (7) и (8)
позволяют определить ток и напряжение
в любой точке линии по их известным
значениям в начале линии. Обычно в
практических задачах бывают заданы
напряжение
![]() и
ток
и
ток![]() в
конце линии. Для выражения напряжения
и тока в линии через эти величины
перепишем уравнения (5) и (6) в виде
в
конце линии. Для выражения напряжения
и тока в линии через эти величины
перепишем уравнения (5) и (6) в виде
|
|
(9) |
|
|
(10) |
Обозначив
![]() и
и![]() ,
из уравнений (9) и (10) при
,
из уравнений (9) и (10) при![]() получим
получим
![]()
![]()
откуда
![]()
![]()
После подстановки
найденных выражений
![]() и
и![]() в
(9) и (10) получаем уравнения, позволяющие
определить ток и напряжение по их
значениям в конце линии
в
(9) и (10) получаем уравнения, позволяющие
определить ток и напряжение по их
значениям в конце линии
|
|
(11) |
|
|
(12) |
Координату
![]() обозначают
еще какy.
обозначают
еще какy.
Уравнения длинной линии как четырехполюсника
В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями
![]() ;
;
![]() .
.
Эти уравнения
соответствуют уравнениям симметричного
четырехполюсника, коэффициенты которого
![]() ;
;![]() и
и![]() ;
при этом условия
;
при этом условия![]() выполняются.
выполняются.
Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.
Определение параметров длинной линии из опытов холостого хода и короткого замыкания
Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ).
При ХХ
![]() и
и![]() ,
откуда входное сопротивление
,
откуда входное сопротивление
|
|
(13) |
При КЗ
![]() и
и![]() .
Следовательно,
.
Следовательно,
|
|
(14) |
На основании (13) и (14)
|
|
(15) |
и
![]() ,
,
откуда
|
|
(16) |
Выражения (15) и
(16) на основании данных эксперимента
позволяют определить вторичные
параметры![]() и
и![]()
![]() линии,
по которым затем могут быть рассчитаны
ее первичные параметры
линии,
по которым затем могут быть рассчитаны
ее первичные параметры![]() ,
,![]() ,
,![]() и
и![]() .
.
Линия без потерь
Линией без потерь
называется линия, у которой первичные
параметры
![]() и
и![]() равны
нулю. В этом случае, как было показано
ранее,
равны
нулю. В этом случае, как было показано
ранее,
![]() и
и
![]() .
Таким образом,
.
Таким образом,
![]()
![]() ,
,
откуда![]() .
.
Раскроем
гиперболические функции от комплексного
аргумента![]() :
:
![]()
![]()
Тогда для линии
без потерь, т.е. при
![]() ,
имеют место соотношения:
,
имеют место соотношения:![]() и
и![]() .
.
Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
|
|
(17) |
|
|
(18) |
Строго говоря,
линия без потерь (цепь с распределенными
параметрами без потерь) представляет
собой идеализированный случай. Однако
при выполнении
![]() и
и![]() ,
что имеет место, например, для
высокочастотных цепей, линию можно
считать линией без потерь и, следовательно,
описывать ее уравнениями (17) и (18).
,
что имеет место, например, для
высокочастотных цепей, линию можно
считать линией без потерь и, следовательно,
описывать ее уравнениями (17) и (18).

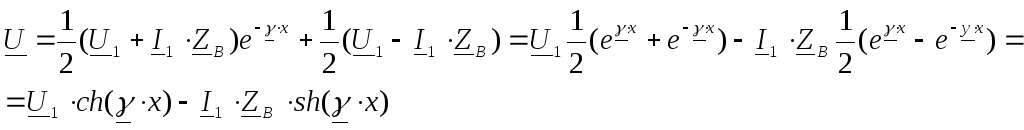
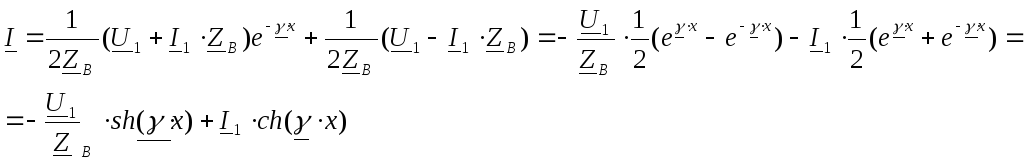
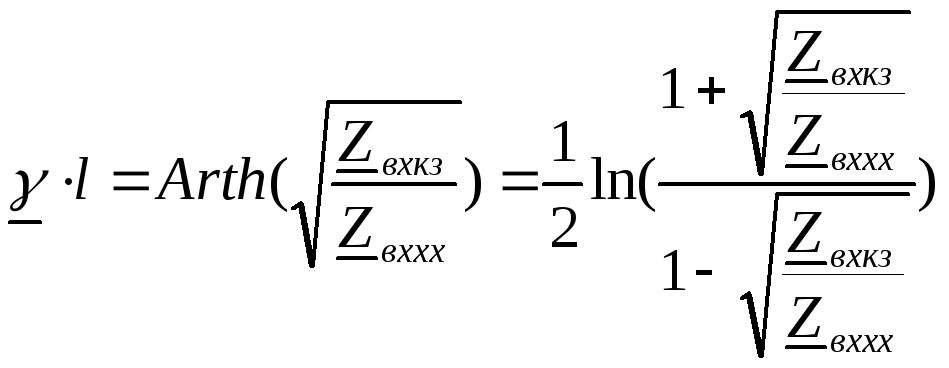 .
.