
Lektsii_Fizika_chast_II
.pdf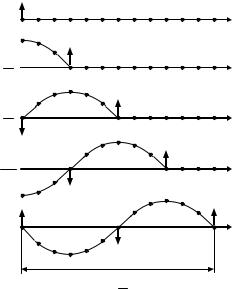
t 0 |
|
X |
Волна, |
колеба- |
||
|
|
|
ния в которой про- |
|||
t T |
|
|
исходят |
лишь |
с |
|
|
X |
одной |
частотой, |
|||
4 |
|
|
называется |
моно- |
||
|
|
|
||||
t T |
|
|
хроматической. |
|
||
|
X |
В |
декартовой |
|||
2 |
|
|
системе |
координат |
||
|
|
|
||||
t 3T |
|
|
положение |
любой |
||
|
X |
колеблющейся |
|
|||
4 |
|
|
|
|||
|
|
точки в заданный |
||||
|
|
|
||||
|
|
|
момент |
времени |
t |
|
t T |
|
X |
задаётся |
с |
помо- |
|
|
|
|
щью координат x, y |
|||
T |
|
и z. |
|
|
|
|
|
|
|
Смещение от |
|||
|
|
положения равно- |
||||
|
|
|||||
|
|
весия точки, име- |
||||
|
|
|
||||
Рис. 5.1 |
|
ющей координаты |
||||
|
|
|
x, y и z в заданный |
|||
момент времени t, описается с помощью функции, которая назы-
вается волновой:
(x, y, z, t).
5.2Уравнение бегущей волны
a)Выведем уравнение плоской волны, распространяющейся вдоль выбранной оси X, рис. 5.1.
Пусть в начале координат (при x 0) частицы упругой среды совершают колебания по закону (t) Acos( t ). Плоская волна распространяется в положительном направлении оси X, при этом в колебания вовлекаются всё новые и новые частицы. Очевидно: чем дальше от начала координат находятся эти частицы, тем позже они окажутся вовлечёнными в колебательное движение. Время запаздывания x/ , где x – координата этих точек по
30
оси X, а – скорость волны. Сказанное означает, что колебания в плоскости, находящейся на расстоянии x от начала координат, происходят по закону
|
(x, t) Acos[ (t ) ]. |
|
|
|||||
Преобразуем это выражение: |
|
|
|
|
|
|
||
(x,t) Acos[ t |
x |
] Acos[ t |
|
2 |
x ] Acos[ t |
2 |
x ] |
|
|
|
|
||||||
и введём обозначение |
|
|
|
|
|
|
||
|
|
k |
2 |
|
(5.2) |
|||
|
|
|
||||||
|
|
|
|
|
||||
(параметр k называется волновым числом).
Мы получили уравнение плоской волны, распространяющейся в положительном направлении оси X, позволяющее рассчи-
тать, каким окажется в заданный момент времени t смещение от положения равновесия точек, имеющих координату x вдоль этой оси:
(x, t) Acos( t kx ). |
(5.3) |
|
|
Аналогично можно показать, что для плоской волны, распространяющейся в направлении, противоположном направлению оси X, справедливо уравнение:
(x, t) Acos( t kx ). |
(5.4) |
b) Уравнение сферической волны (фронтом которой является сфера с центром в точке – источнике колебаний) имеет следующий вид:
(r, t) |
A |
sin( t kr ), |
(5.3) |
|
|||
|
r |
|
|
|
|
|
|
где r – расстояние от источника колебаний до интересующей нас точки (то есть – радиус сферы). Уравнение справедливо для расстояний r .
Заметим: амплитуда колебаний плоской волны не зависит от расстояния до источника колебаний; амплитуда колебаний в сферической волне уменьшается по мере удаления от источника.
31

5.3 Дифференциальное волновое уравнение
Вспомним: для получения формул, описывающих разные виды колебаний, мы вынуждены были каждый раз составлять и решать дифференциальное уравнение, которое, в принципе, имело одну и ту же структуру (линейное дифференциальное уравнение второго порядка). Примерно так же дело обстоит и в случае формул для функций (x, y, z, t), описывающих разные виды волн: все они являются результатом решения (правда, – со своими добавочными условиями: граничными, начальными и так далее), уравнения вида
2 |
|
2 |
|
2 |
|
1 |
2 |
, |
(5.5) |
|
x2 |
y2 |
z2 |
2 |
t 2 |
||||||
|
|
|
|
|
которое называется дифференциальным волновым уравнением
(здесь – скорость волны).
Используя обозначения |
2 |
|
|
2 |
|
|
2 |
(здесь знак |
|
x2 |
y2 |
z2 |
|||||||
|
|
|
|
||||||
означает оператор Лапласа или «лапласиан») и 2 , диф-
t 2
ференциальное волновое уравнение можно переписать в виде:
|
1 |
|
2 |
|
В виде примера покажем, что формула (5.3) для плоской волны, распространяющейся вдоль оси OX, действительно является решением уравнения вида (5.5):
(x, y, z, t) (x, t) Acos( t kx ),
2 |
k2Acos( t kx ); |
2 |
0, |
|
|
2 |
0, |
||||
x2 |
y2 |
|
|
z2 |
|
||||||
|
|
|
|
|
|
|
|
||||
2 |
2Acos( t kx ); |
|
|
|
|
|
2 |
|
|
|
, и, действи- |
t 2 |
T |
2 |
|
T |
k |
||||||
|
|
|
|
|
|
||||||
тельно, k2Acos( t kx ) 0 0 k 2 2Acos( t kx ).
32
5.4 Упругие волны
Упругие волны – волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил. В жидких и газообразных средах могут распространяться только продольные волны, в твёрдых телах упругие волны могут быть не только продольными, но и поперечными.
Скорость распространения упругих волн зависит от плотности среды : ½, при этом коэффициенты пропорциональности в этой зависимости могут быть разными для продольных и поперечных волн, то есть в твёрдых телах скорости распространения поперечных и продольных волн в общем случае неодинаковы.
В упругих средах различными оказываются и скорости волн, имеющих разные частоты. Мы говорили ранее, что результат сложения колебаний, происходящих в одном направлении с близкими частотами, называется биениями. Если в веществе распространятся две волны с близкими частотами, но с разными скоростями, то движется (причём – с собственной скоростью) и максимум возникающего биения.
Напомним: скорость каждой из складывающихся волн называются фазовой, её рассчитываем по формуле
|
|
|
2 |
|
|
. |
|
T |
|
2 |
|||
|
T |
|
|
k |
Можно показать, что скорость движения максимума, возникающего при сложении группы волн с близкими частотами
Г |
d |
; |
(5.6) |
|
|||
|
dk |
|
|
|
|
|
|
эта скорость называется групповой скоростью.
Понятно, что движение подобного максимума – просто результат математических вычислений, реально в пространстве распространяются лишь формирующие его волны, поэтому не удивительно, что групповая скорость по величине может оказаться как меньше фазовой скорости каждой из волн, так и больше их.
33

Позднее мы увидим, что зависимость скорости распростра-
нения волны от её частоты (или длины волны ) приводит к явлению, которое называется дисперсией.
Существенной особенностью волнового движения является то, что энергия колебаний каждого малого участка упругой среды
периодически меняется со временем. В этом заключается принципиальное отличие волнового движения от свободных механи-
ческих колебаний, полная энергия которых не зависит от времени (просто кинетическая энергия переходит в потенциальную и наоборот). Это приводит к тому, что волна переносит энергию в пространстве, вовлекая в колебательное движение всё новые и новые объекты.
Описание процесса распространения энергии в различных средах имеет важное практическое значение. Но энергия – скаляр, поэтому для математического описания, как её величины, так и того, куда она распространяется, вводится специальный вектор
плотности потока энергии (вектор Умова).
Пусть за время t через поверхность dS, перпендикулярную
направлению вектора скорости фронта волной переносится энергия dW. Если учесть, что за это время фронт проходит расстояние x t, то можно записать:
dW |
|
dW |
x |
dW |
w , |
dS t |
|
dS x t dV |
|||
где w – объёмная плотность энергии: так, для упругой волны, распространяющейся в среде с плотностью , w A2 2sin2( t kx ).
Вектором Умова называется вектор
|
|
(5.7) |
u |
w , |
численно равный энергии, переносимой в единицу времени через единичную площадку, перпендикулярную направлению потока энергии в данной точке; направление вектора совпадает с векто-
ром .
Интенсивностью волны называется модуль среднего значения вектора Умова:
2 2 2 1 2 2
I | u | | A sin ( t kx ) | A .
2
34
5.5 Эффект Доплера (в акустике)
Эффект Доплера заключается в изменении частоты волны, воспринимаемой приёмником, при движении источника и приёмника волн относительно друг друга.
Пример: источник и приёмник звука ( 0 T0) движутся вдоль соединяющей их прямой со скоростями uИ и uП, соответственно.
Если движется только источник навстречу приёмнику, то за время T0 фронт, идущий к приёмнику, успеет отдалиться от источника на расстояние 0 uИT0: приёмник воспримет сигнал с частотой
|
1 |
|
|
|
|
|
|
|
|
|
/T0 |
|
0 |
|
|
. |
T |
|
|
0 |
u T |
|
/T u |
И |
u |
|
|||||||
|
|
|
|
|
|
И |
0 |
0 |
0 |
|
|
И |
||||
Если источник движется в сторону от приёмника, 0 uИT0,
|
1 |
|
|
|
|
|
|
|
|
|
/T0 |
|
0 |
|
|
. |
T |
|
|
0 |
u T |
|
/T u |
И |
u |
|
|||||||
|
|
|
|
|
|
И |
0 |
0 |
0 |
|
|
И |
||||
В случае, когда источник неподвижен, а приёмник движется навстречу источнику, «с точки зрения приёмника» волна распространяется быстрее, * 0/T0 uП, или
|
1 |
|
|
0 / T0 uП |
uП 0 |
uП . |
|
||||||
|
T |
0 |
0 |
T0 |
|
|
При движении приёмника в сторону от источника
|
1 |
|
|
0 / T0 uП |
|
uП 0 |
uП . |
|
0 |
||||||
|
T |
0 |
|
T0 |
|
||
В результате можно записать: если движутся и источник, и приёмник, частота воспринимаемого приёмником сигнала рассчитывается по формуле
0 |
uП . |
(5.8) |
|
uИ |
|
Верхние знаки в этой формуле соответствуют сближению источника и приёмника, а нижние – их расхождению друг от друга.
35
Примером проявления эффекта Доплера является изменение тона свистка электропоезда в момент прохождения мимо наблюдателя на платформе: при приближении поезда частота выше (знак «минус» в знаменателе дроби), при его удалении частота звука скачком понижается («минус» меняется на «плюс»).
Приборы, работа которых основана на данном эффекте, широко применяются на транспорте, в медицине и т. д.
Эффект Доплера применяется для оценки скорости движения источника и приёмника света, например, при изучении звёздных систем.
Контрольные задания и вопросы
1.Что называется волной? Какая волна называется упругой?
2.Какие волны называются продольными? Поперечными? Приведите примеры волн обоих типов.
3.Дайте определение фронта волны. Какие волны называются плоскими? Какие волны называются сферическими?
4.Что называется длиной волны? В каких единицах она измеряется в СИ?
5.Запишите уравнение плоской бегущей волны. Введите понятие волнового числа.
6.Запишите дифференциальное волновое уравнение и поясните смысл входящих в него параметров.
7.Чем отличаются фазовая и групповая скорости волн? Какая волна называется монохроматической?
8.Дайте определение вектора плотности потока энергии (вектора Умова). Каковы единицы его измерения?
9.Что такое «интенсивность» волны?
10.В чём заключается эффект Доплера?
36

Лекция № 6 |
ВОЛНЫ. ЧАСТЬ II |
6.1 Сложение волн
Если в среде одновременно распространяются несколько волн, в которых колебания происходят в одном направлении, то, согласно принципу суперпозиции, в каждой точке пространства малые колебания, создаваемые этими волнами, складываются друг с другом.
Явление возникновения устойчивой во времени картины распределения в пространстве максимумов и минимумов колебаний при сложении двух или большего числа волн называется интер-
ференцией волн.
Получим условие, при котором картина будет устойчивой во времени.
Пусть в некоторой точке пространства в какой-то момент времени t складываются две плоские волны с одинаковыми амплитудами A, колебания в которых происходят в одном направлении; путь одной из волн от источника до точки встречи равен l1, путь дугой равен l2:
1 Acos( 1t k1l1 1),
2 Acos( 2t k2 l 2 2),
В этой точке возникает результирующее колебание, амплитуда которого AРЕЗ рассчитывается по формуле (4.1), согласно которой
AРЕЗ 
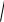 A2 A2 2A2cos( 2t k2l2 2 1t k1l1 1) .
A2 A2 2A2cos( 2t k2l2 2 1t k1l1 1) .
Для того чтобы картина не менялась со временем, необходимо, чтобы амплитуда AРЕЗ не зависела от t. Очевидно, это возможно лишь в случае, когда выполняется условие:
1t 2t 0, или 1 2.
Таким образом, интерферировать могут лишь волны одинако-
вой частоты (или имеющие одинаковую длину волны: T/ 2 / и одинаковое волновое число k 2 / ).
Заметим: если разность фаз интерферирующих волн равна 2 m, ( 2t k2l2 2) ( 1t k1l1 1) 2 m,
37

где m 0, 1, 2, 3…, то, с учётом того, что 1 2 , (и, следовательно, k1 k2 k)
k(l2 l1) ( 2 1) 2 m.
Амплитуда установившихся колебаний будет максимальна.
Если при этом ещё 1 2, то, с учётом того, что k 2 / , условие возникновения максимума интерференционной картины приобретает следующий вид:
l2 l1 m . |
(6.1) |
Разность l2 l1 называется геометрической разностью хода;
максимум возникает, если геометрическая разность хода равна «целому числу длин волн».
Аналогично можно получить условие минимума: он возникает, если разность фаз интерферирующих волн
k(l2 l1) ( 2 1) 2 m,
или геометрическая разность хода равна «нечётному числу
длин полуволн»: |
|
|
l2 l1 |
(2m 1) . |
(6.2) |
|
2 |
|
|
|
|
Заметим: для возникновения устойчивой картины нужно не только, чтобы были равны частоты интерферирующих волн ( 12), но и разность 1 2 была постоянной. Таким образом, интерферировать могут лишь волны, создающие колебания в одном
направлении, и разность фаз ( 2t k2l2 2) ( 1t k1l1 1) которых в каждой точке пространства не зависит от времени.
Волны, разность фаз которых не зависит от времени, называются когерентными.
6.2 Стоячие волны
Частным случаем интерференции волн являются стоячие вол-
ны. Стоячая волна – это результат сложения бегущей волны с собой самой, например, отражённой от препятствия и бегущей в противоположную сторону.
38
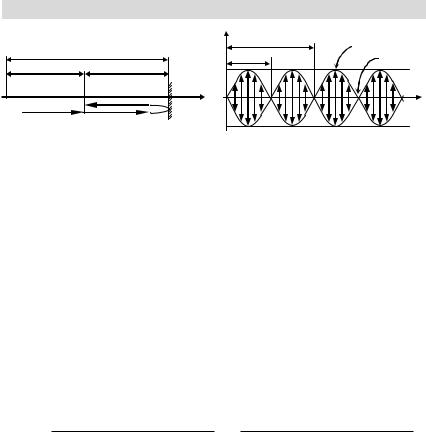
Пусть, например, плоская волна распространяется в положительном направлении оси X (см. рис. 6.1):
|
|
1 Acos( t kx ). |
(6.3) |
|
|
|
|
|
ПУЧНОСТЬ |
|
l |
l x |
С ½ |
УЗЕЛ |
|
x |
|
|
|
0 |
x |
l X 0 |
|
X |
|
Рис. 6.1 |
|
Рис. 6.2 |
|
Дойдя до стенки, находящейся на расстоянии l от начала оси координат, волна отражается и идёт обратно. В точке с координатой x складываются колебания, порождаемые волной (6.3) и отражённой волной 2, которая успевает к этому времени пройти расстояние l (l x). Кроме того, при отражении от более плотной среды волна получает добавочный сдвиг по фазе (при отражении от менее плотной среды этого сдвига не возникает, то есть можно написать, что 0).
В итоге отражённая волна создаёт в точке с координатой x колебание вида
2 Acos{ t k[l (l x)] }. |
(6.4) |
Используя известные тригонометрические соотношения, для результирующего колебания получим:
1 2 Acos( t kx ) Acos{ t k[l (l x)] }
2Acos (t kx ) [t k(2 l x) ] cos (t kx ) [t k(2 l x) ] 2 2
2Acos[k(l x) ½ ]cos( t kl ½ ) AРЕЗcos( t *),
где AРЕЗ 2Acos[k(l x) ½ ], * ( kl ½ ).
Мы видим: в каждой точке оси X возникают гармонические колебания, амплитуда которых 2Acos[k(l x) ½ ] зависит от местоположения точки. Так, на оси существуют точки, в которых разность k(l x) ½ m (здесь m – целое число), и колебания имеют наибольшую амплитуду: AРЕЗ 2A. В точках, для которых
39
