
Lektsii_Fizika_chast_II
.pdfисчезает вовсе. При анализе кривых следует помнить, что уравнение (14.7) является лишь очередным приближением в описании поведения реального газа. На деле связь давления с объёмом описывается линией, близкой той, которая представлена на рис. 14.4б: при сжатии газа, начиная с точек 1 и 1 на рис. 14.4а, в сосуде возникает жидкая фаза, причём, чем сильнее сжимается газ, тем её больше. Давление практически не растёт вплоть до точек 2 и 2 , когда весь газ превращается в жидкость. Далее изотерма описывает поведение уже не газа, а жидкости, которая сжимается плохо, о чём говорит крутизна графика в области малых V.
При температурах выше TКР, а также в области больших V реальный газ ведёт себя, как идеальный.
Контрольные задания и вопросы
1.Какой газ называется идеальным? Запишите уравнение Клапейрона – Менделеева, поясните смысл и укажите единицы измерения входящих в него величин.
2.Что такое 1 моль?
3.Выведите формулу, связывающую давление идеального газа с концентрацией его молекул.
4.Какие процессы называются изопроцессами? Начертите графики этих процессов в координатах p – V, p – T, V – T.
5.Оцените размер молекулы газа.
6.В чём заключается закон Дальтóна? Приведите пример проявления закона.
7.Чем поведение реального газа на практике отличается от поведения идеального газа?
8.Начертите графики изотермы реального газа в координатах p – V для нескольких значений температуры.
130
Лекция № 15 |
МОЛЕКУЛЯРНАЯ ФИЗИКА |
|
И ТЕРМОДИНАМИКА. ЧАСТЬ II |
15.1 Основное уравнение молекулярно-кинетической теории газов
Основное уравнение молекулярно-кинетической теории (МКТ) позволяет связать друг с другом параметры идеального газа: макроскопические (те, которые обычно измеряются на практике, например – давление) и микроскопические (характеризующие движение отдельных молекул, например, их скорость). Это уравнение впервые было получено Клаузиусом; в основе вывода лежат следующие положения.
1.Давление газа объясняется ударами молекул о дно и стенки сосуда.
2.Давление p тем больше, чем больше количество ударов. Но количество ударов определяется концентрацией молекул n, зна-
чит, давление зависит от концентрации: p n, где n N/V (здесь
N – число молекул в сосуде объёмом V).
3. Давление тем больше, чем больше кинетическая энергия молекулы, налетающей на стенки сосуда. Значит, давление зави-
сит от массы m молекул и квадрата их скорости 2: p m 2.
4. Для молекул газа, находящегося в замкнутом сосуде, все направления равновероятны, поэтому вдоль любого из них (вдоль осей X, Y и Z) в каждый момент времени компоненты скорости имеет лишь треть молекул: p ⅓m 2
5. Молекул много, они движутся с различными скоростями и в различных направлениях, причем далеко не все из них принимают участие в создании давления на конкретный участок стенок сосу-
да. Это означает: при расчётах скорости молекул следует усреднить.
Для получения уравнения используем метод размерностей: давление p измеряется в паскалях, 1 Па 1 Н м 2 1 кг с 2 м 1; концентрация n измеряется в м 3;
масса m измеряется в килограммах (кг); скорость измеряется в метрах в секунду (м с 1).
131

Комбинируя размерности, можно сделать вывод о том, что равенство левой и правой частей уравнения достигается, если его записать в виде: кг с 2 м 1 м 3 кг (м с 1)2, то есть
p nm 2.
Строгий вывод формулы приводит к следующему виду основ-
ного уравнения МКТ газов:
p |
1 |
nm КВ2. |
(15.1) |
|
3 |
||||
|
|
|
||
|
|
|
|
Здесь учтён множитель ⅓, о котором говорилось выше, и проведено усреднение квадратов скоростей всех N молекул:
|
|
|
|
|
|
|
|
|
|
|
N |
2 |
|
|
|
|
|
2 |
|
2 |
|
2 |
|
i |
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
КВ2 1 |
2 |
|
... N |
|
|
i 1 |
. |
|||||
|
|
|
N |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
2 |
|
|
|
|
|
|
|
|
|
Скорость КВ |
|
i |
|
|
|
|
|
|
|
|
|
||
i 1 |
|
|
называется среднеквадратичной, она |
||||||||||
N |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
характеризует среднюю кинетическую энергию хаотического поступательного движения молекул газа.
Очевидно: общая кинетическая энергия хаотического поступательного движения молекул газа
WК |
m |
2 |
… |
m |
|
2 |
|
Nm[( 2 |
,.. |
2 ) / N ] |
|
M |
|
2 |
|
1 |
|
|
N |
|
1 |
|
N |
|
КВ |
|
, |
||||
|
2 |
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
||
где M Nm nVm – общая масса всех молекул, поэтому уравнение (15.1) может быть представлено в виде
|
|
|
|
pV |
2 |
WК, |
|
|
|
|
|
|
(15.2) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
m КВ |
2 |
|
2 |
|
или, согласно формулам (15.1) и (15.2), p |
n |
|
|
n‹wК*›, |
|||||||||
3 |
2 |
|
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
m |
|
2 |
|
|
|
|
|
|
|
|
|
|
где ‹wК*› |
КВ |
|
– средняя кинетическая энергия поступатель- |
||||||||||
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ного движения одной молекулы.
132
Таким образом, давление идеального газа равно двум третям энергии поступательного хаотического движения молекул, находящихся в единице его объёма.
Примечание 1
|
M КВ |
2 |
|
|
|
|
|
Μ |
|
|
Поскольку WК |
|
, и для идеального газа pV |
RT, |
|||||||
|
|
|||||||||
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
можно сделать вывод о том, что КВ |
3RT |
|
, или, с учётом соот- |
|||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
||
ношений k R/NА, mNА (здесь k – постоянная Больцмана, NА – число Авогадро),
КВ |
|
3kT |
|
. |
(15.3) |
|
|||||
|
|
m |
|
||
При этом средняя кинетическая энергия ‹wК*› поступательного хаотического движения молекулы любого идеального газа определяется только его температурой и не зависит от природы самого газа:
|
m |
|
2 |
|
3 |
|
‹wК*› |
КВ |
|
|
kT. |
||
2 |
|
2 |
||||
|
|
|
|
|||
Мы видим, что термодинамическая температура характеризует скорость поступательного хаотического движения молекул газа или соответствующую этой скорости кинетическую энергию.
Молекулы могут не только двигаться поступательно, но вращаться и колебаться: как мы отметим далее, энергия этих видов движения также зависит лишь от T.
Ситуация, при которой все молекулы вещества покоятся, в классической физике соответствует абсолютному нулю температуры.
15.2 Распределение Максвелла молекул по скоростям
В каждый конкретный момент времени молекулы газа имеют различные скорости: одни движутся быстрее, другие – медленнее,
133

есть и такие, которые в этот момент практически остановились. Задачу о распределении молекул идеального газа по скоростям поступательного движения впервые теоретически решил Дж. Максвелл. Он показал, какое число dN из общего числа молекул N, при данной температуре T обладает скоростью, значение модуля которой принадлежит интервалу d в пределах от до d . Соответствующая формула имеет вид:
|
|
|
|
|
|
|
|
3 |
|
|
m 2 |
|
|
|
|
|
|||
dN N |
|
m |
|
|
|
2 |
|
|
4 2d . |
|
|||||||||
|
|
e |
|
2kT |
(15.4) |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dN |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
m 2 |
|
|
|
|
|
|
|
|
m |
|
|
|
2 |
|
|
|
|
|||||
F( ) |
|
|
N |
|
|
|
|
e |
2kT 4 2 |
(15.5) |
|||||||||
d |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2kT |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называется полной статистической функцией распределения мо-
лекул по скоростям.
Очевидно: при 0 и F( ) 0; при F( ) 0. Из усло-
вия dF 0 можно найти значения , соответствующие экстре- d
мумам функции. Легко показать, что при 0 имеет место минимум: F( ) 0; максимальному значению F( ) соответствует наиболее вероятная (чаще других встречающаяся) скорость
ВЕР |
|
2kT |
|
. |
|
|
(15.6) |
||||
|
|
|
|||||||||
|
|
m |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Зная вид функции F( ), дли модуля можно определить сред- |
|||||||||||
|
|
|
|
|
|
|
|
||||
нюю арифметическую скорость молекул газа: ‹ › |
|
8 |
|
kT |
|
. И |
|||||
|
|
||||||||||
|
|
|
|
|
|
|
m |
||||
наиболее вероятная, и средняя арифметическая скорости, так же, как и среднеквадратичная, зависит от температуры, при этом
ВЕР ‹ › 1,13 ВЕР КВ 1,22 ВЕР.
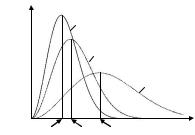
Графики полной статистической функции распределения молекул идеального газа по скоростям для трёх значений температуры представлены на рис. 15.1.
134
F( ) |
T1 |
|
|
Из рисунка следует: |
||
|
|
- |
чем выше температура, |
|||
|
|
|
|
|||
|
|
T2 T1 |
|
тем больше ВЕР, но молекулы, |
||
|
|
|
обладающие этой |
скоростью, |
||
|
|
|
|
|||
|
|
|
T3 T2 T1 |
встречаются реже, то есть со- |
||
|
|
|
|
ответствующее значение F( ВЕР) |
||
|
|
|
|
становится меньше. |
||
0 ВЕР1 |
ВЕР2 |
ВЕР3 |
|
- |
При неизменном коли- |
|
|
Рис. 15.1 |
|
честве молекул |
N площади |
||
|
|
под кривыми на рис. 15.1 оди- |
||||
|
|
|
|
|||
наковы, поскольку эти площади численно равны этому количеству:
|
|
dN |
|
|
|
F ( )d |
d |
dN N const. |
|||
|
|||||
0 |
0 |
d |
0 |
||
|
|
||||
Ещё раз отметим: закон Максвелла – статистический, то есть выполняется тем точнее, чем больше N. Он справедлив лишь для хаотического (теплового) движения молекул идеального газа.
Примечание 2
Об атмосфере планет. При функция F( ) хотя и стремится к нулю, но остаётся больше него, а это означает, что среди молекул газа атмосферы, окружающей планету, должны встречаться такие, скорость которых больше, чем вторая космическая для данной планеты. Такие молекулы способны улететь в космос, и атмосфера планеты будет «таять». Существенно, что снижение числа молекул в газе при данной температуре приводит лишь к уменьшению площади под кривой на графике функции F( ), сама же форма кривой не меняется: после ухода быстрых молекул появляются новые с такими же скоростями, которые тоже покидают атмосферу, и так далее. В итоге любая планета должна со временем потерять свою атмосферу. Процесс идёт тем быстрее, чем меньше масса планеты (ниже значение второй космической скорости), поэтому, например, пытаться создать атмосферу вокруг астероидов смысла не имеет.
135

Потери могут компенсироваться в результате выбросов газа из недр планет. Так, потери земной атмосферы полностью перекрываются поступлением газов из недр Земли при тектонических процессах (извержениях вулканов, землетрясениях и так далее). На Марсе, например, подобных явлений не наблюдается, и это – одна из причин, по которым его атмосфера является гораздо более разрежённой, чем земная.
15.3 Опыт Штерна
Экспериментальное подтверждение справедливости закона Максвелла впервые дал. Штерн. Опыт Штерна заключался в следующем.
По платиновой проволоке, покрытой слоем серебра, пропускался электрический ток. Проволока нагревалась, серебро испарялось: пары серебра, испускаемые проволокой, играли роль идеального газа. Вокруг проволоки располагались два цилиндра с радиусами r1 и r2 так, что их оси совпадали с проволокой (схема установки, вид сверху, показана на рис. 15.2). В цилиндре меньшего радиуса была прорезана щель, параллельная его оси; атомы серебра, пролетев сквозь щель, оседали на внутренней поверхности большого цилиндра, формируя тёмную полоску – чёткое изображение щели (рис. 15.а).
Изображение фиксировалось при неподвижных цилиндрах, а затем сравнивалось с тем, которое получалось в случае, когда оба цилиндра начинали вращаться относительно проволоки с одинаковой угловой скоростью . Из-за того, что пролёт промежутка между цилиндрами занимает некое время, изображение щели на его внутренней поверхности большого цилиндра оказывается смещённым на угол , такой, что
r2 r1 ,
где – скорость атомов серебра, вылетевших из щели.
136
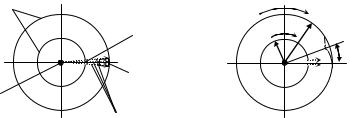
Цилиндры |
|
|
|
|
Щель |
|
r2 |
|
|
||
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
Изображение |
|
|
|
|
|
|
Проволока |
щели |
|
|
|
|
|
|
|
Атомы серебра |
|
|
|
а) |
|
б) |
Рис. 15.2
Если бы скорости всех атомов были одинаковы, изображение щели всё равно получалось бы чётким. Но скорости у атомов – разные, причём, чем больше , тем меньше оказывается угол (рис. 15.2б). Анализируя угловое распределение плотности осажденного серебра (по степени потемнения поверхности цилиндра), можно сделать вывод о распределении атомов серебра по скоростям. Сопоставление результатов эксперимента с теоретическими расчётами подтвердило правильность выводов Максвелла.
Примечание 3
Прямая интерпретация результатов опыта Штерна не совсем корректна: распределение Максвелла справедливо для хаотического движения частиц, а в опыте сравнивались скорости их направленного движения. Учёт этого фактора необходим при анализе получаемых в ходе опыта данных.
Примечание 4
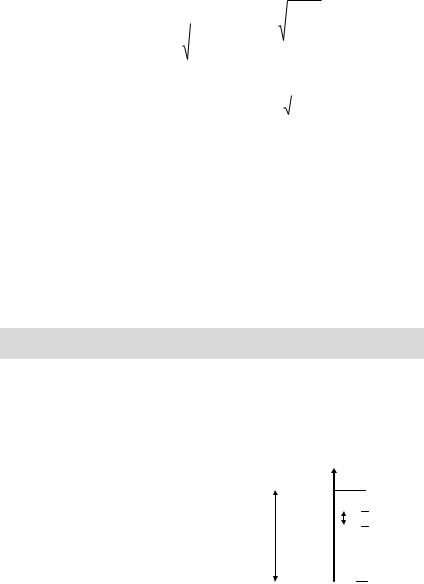
От формулы полной статистической функции распределения молекул газа по скоростям F( ) можно перейти к формуле для полной статистической функции распределения молекул газа по их кинетическим энергиям F(wК). Для этого следует преобразо-
вать выражение (15.5), учитывая, что |
m 2 |
wК, 2 |
2 |
wК, а |
|
2 |
m |
||||
|
|
|
137
d |
2 |
dwК |
|
|
2 |
|
|
dwК |
2 |
dwК. |
m |
|
|
|
|
|
mw K |
||||
|
|
2 |
|
|||||||
|
|
m |
w K |
|
||||||
|
|
|
|
|
|
|||||
|
|
|
m |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
В результате получим:
|
dN |
|
2 |
wК |
|
|
|||
F(wК) |
N |
e kT |
w |
K |
(15.7) |
||||
dw |
|
( kT )3/2 |
|||||||
|
K |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
15.4 Распределение Максвелла-Больцмана
15.4.1 Барометрическая формула
Известно, что чем выше мы поднимаемся над поверхностью Земли, тем разрежённее становится воздух, тем меньше оказывается атмосферное давление. Выведем барометрическую формулу
– уравнение, описывающее, как давление идеального газа меняется с высотой.
Известно, что вертикальный столб газа или жидкости высотой h оказывает на горизонтальную поверхность давление
p gh, |
(15.8) |
где – плотность газа (жидкости), g – ускорение свободного падения. Подъём над поверхностью на высоту dy означает уменьшение на то же dy высоты столба или снижение давления на величину dp – см. рис. 15.3. Если считать, что ни плотность газа (жидкости), ни ускорение свободного падения с высотой практически не меняются, то
dp g dy |
(15.9) |
|
|
|
|
Y |
|
|
|
|
p |
(знак «минус» означает, |
что чем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y dy |
|
|
|
|
p(y) dp |
||||
больше высота подъёма, тем меньше |
|
|
|
|
|
|
|||||
|
|
dy |
|
||||||||
|
|
|
y |
|
|
p(y) |
|||||
становится давление). |
|
h |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Для атмосферы – идеального газа, |
|
|
|
|
|
|
|
|
|
|
|
подчиняющегося закону Клапейрона |
|
|
|
|
|
|
|
|
|
p0 |
|
– Менделеева, можно записать: |
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Рис. 15.3 |
|
|||||
138

p |
M |
RT, |
или p |
|
RT, |
откуда |
p |
. |
|
|
|
||||||
|
V |
|
|
|
|
RT |
||
Подставим полученное выражение для в формулу (15.9): dp p g dy
|
|
|
RT |
|
и преобразуем её к виду |
|
|
||
|
dp |
|
|
g dy. |
|
|
RT |
||
|
p |
|
||
Проинтегрируем левую и правую части уравнения, принимая во внимание, что при y 0 давление равно некоторому значению p0, а при y h давление равно искомому p (параметры , g и T будем считать постоянными):
p |
dp |
h |
|
|
||
|
|
|
|
gdy , или |
|
|
p |
RT |
|
||||
p0 |
|
0 |
|
|
|
|
|
p p0 e |
gh |
|
|||
|
RT . |
(15.10) |
||||
Мы получили барометрическую формулу, показывающую, как атмосферное давление меняется с высотой подъёма над земной поверхностью. Учитывая, что молярная масса NАm, а R NАk, где m – масса молекулы, NА – число Авогадро, а k – постоянная Больцмана, барометрическую формулу можно переписать в виде
mgh |
|
p p0 e kT . |
(15.11) |
15.4.2 Распределение Больцмана
Сделаем следующий шаг.
Поскольку для идеального газа справедлива формула p nkT, где n – концентрация молекул, из (15.11) следует, что
mgh |
|
n n0 e kT . |
(15.12) |
139
