
Lektsii_Fizika_chast_II
.pdf
Лекция № 2 КОЛЕБАНИЯ. ЧАСТЬ II
2.1 Затухающие колебания
Учтём теперь то, что в реальной системе всегда имеют место силы трения, сопротивления. Наличие таких сил отражается введением добавочных слагаемых в исходные формулы, описывающей поведение системы со временем (то есть в уравнения второго закона Ньютона, основного закона динамики вращательного движения, закона Ома). При небольших скоростях величина сил трения, сопротивления пропорциональна скорости движения тела:
|FТР| | |, или |FТР| | x |, поэтому, с учётом того, что векторы скорости и силы сопротивления направлены в противоположные сто-
роны, можно записать: FТР r x , где r – коэффициент сопротивления.
Уравнение второго закона Ньютона для пружинного маятника:
kx r x m x . |
(2.1) |
Приведём данное дифференциальное уравнение к канониче-
скому виду: |
x |
|
r |
x |
|
k |
|
x 0, и, обозначив |
r |
, 0 |
|
|
k |
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
m |
|
|
|
2m |
|
|
|
m |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
2 x |
0 |
2 |
x 0. |
|
|
|
(2.2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Множитель называется коэффициентом затухания; [ ] c 1.
Рассмотрим теперь электрический колебательный контур (рис. 2.1). Запишем для него формулу закона Ома и учтём, что в реальности сопротивлением R его элементов пренебречь нельзя:
|
IR 2 1 |
EСИ, но EСИ L I |
, I q , |
I |
q , С q/( 1 2), |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
причём 1 2 U, следовательно, |
||||||||
|
|
|
1 |
|
2 |
I |
|
q R |
q |
L q . |
(2.3) |
||||
|
|
|
|
||||||||||||
R |
|
|
C |
|
C |
||||||||||
|
|
K |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Приведём данное дифференциальное уравне- |
|||||||||||
|
|
|
|
L |
|
ние к каноническому виду: |
q |
R |
q |
1 |
q 0 |
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
EСИ |
|
|||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
L |
LC |
|||||
|
Рис. 2.1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
10
и, введя обозначения |
R |
|
, 0 |
|
1 |
|
, запишем окончательно: |
||
|
|
|
|||||||
|
|
|
|
||||||
|
2L |
|
|
LC |
|
||||
q |
2 q |
0 |
2 |
q 0. |
(2.4) |
||||
|
|
|
|
|
|
|
|
||
Уравнения (2.2) и (2.4) идентичны, поэтому и их решение должно описываться одинаковыми формулами. Однако сам вид этих формул зависит от того, какой из параметров, входящих в уравнения, больше: 0 или .
Затухающие колебания (случай 0 )
Решение уравнения вида (2.2) в этом случае можно записать так:
x A0e t cos( t ); |
(2.5) |
||
|
|
|
|
здесь использовано обозначение |
|
2 2 . |
|
|
0 |
|
|
Формула (2.5) описывает процесс, который называется зату-
хающими колебаниями. Амплитуда этих колебаний A A0e t
уменьшается со временем тем быстрее, чем больше коэффициент затухания . Циклическая частота этих колебаний меньше, чем она была бы в отсутствие сопротивления ( 0), а период –
больше: T |
|
2 |
T0 |
2 |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
T0 |
|
|
|
T |
|
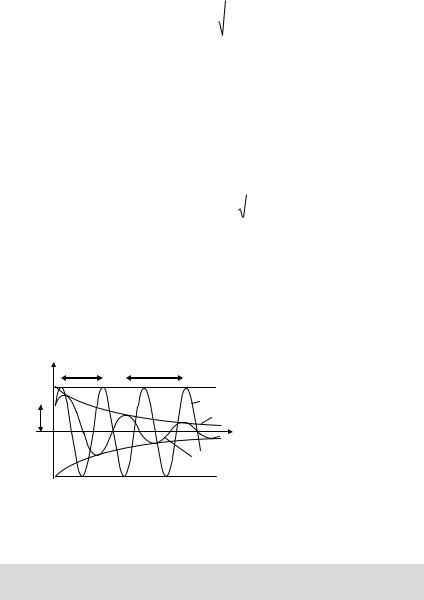
Графики |
сво- |
|||||
|
|
|
|
|
|
бодных |
незатуха- |
||||||||
|
A0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
A0cos(0t 0) |
ющих |
и |
затухаю- |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
A0cos 0 |
|
|
|
|
|
|
|
|
A0e t |
щих |
колебаний |
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
t |
приведены |
на |
|||
|
|
|
|
|
|
|
|
|
рис. 2.2. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
A0e tcos( t 0) |
Перемен- |
|||
A0 |
|
|
|
|
|
|
|
|
ная x |
может |
яв- |
||||
|
|
|
|
|
|
|
|
ляться |
|
координа- |
|||||
|
|
|
|
|
|
|
Рис. 2.2 |
|
|||||||
|
|
|
|
|
|
|
той |
пружинного |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
маятника – см. уравнение (2.2), а может – зарядом конденсатора, см. уравнение (2.4) или (так как U q/C) – напряжением на нём.
Параметры, характеризующие затухающие колебания:
– коэффициент затухания, [ ] c 1;
11

1/ – время релаксации (за которое амплитуда уменьшается в e раз);
|
A(t) |
– декремент затухания (или |
A e |
t |
|
A e T ); |
|
|
0 |
|
|||||
A(t T ) |
A e t T ) |
||||||
|
|
|
0 |
||||
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
ln – логарифмический декремент затухания (очевидно, что
T).
Постепенное уменьшение амплитуды обусловлено постепенной потерей (диссипацией) энергии. Для количественного описания подобных потерь используется энергетическую характери-
стику Q, которая называется добротностью колебательной системы.
По определению добротностью называется домноженное на 2 отношение энергии, запасённой системой в некоторый момент времени, к энергии, теряемой за следующий период колебаний:
Q 2 |
E(t) |
. |
(2.6) |
|
|
||||
E(t) E(t T ) |
||||
|
|
|
Пусть, например, в колебательном контуре в некоторый момент времени заряд конденсатора максимален, q(t) A0e t (при
этом ток в катушке индуктивности I 0), тогда энергия системы
E(t) WЭ макс(t) q(t)2/(2C) A02 e 2 t/(2C).
Через период энергия, запасённая в контуре, становится меньше:
E(t T) WЭ макс(t T) q(t T)2/(2C) A02 e 2 (t T)/(2C), тогда:
|
E(t) |
|
A 2e 2 t |
1 |
|
|
Q 2 |
|
2 |
0 |
2 |
|
. |
E(t) E(t T ) |
A02e 2 t A02e 2 (t T ) |
1 e 2 T |
||||
При малом затухании (2 T 1) можно записать: e 2 T 1 2 T,
или
Q |
|
|
|
|
0 |
. |
(2.7) |
|
|
|
Τ |
|
2 |
|
|
На практике коэффициент затухания часто мал, 2 T 1, и формула (2.7) хорошо описывает связь между добротностью Q и логарифмическим декрементом затухания .
Заметим: и Q, и размерности не имеют.
12
Апериодический процесс (случай 0)
Если 0, решение дифференциального уравнения вида (2.2) записывается следующим образом:
|
|
|
|
|
|
|
|
|
|
x A0 e( |
2 0 2 )t |
B0 e( 2 0 2 )t , |
|
(2.8) |
|||||
x |
|
|
где A0 |
и B0 |
– константы, значе- |
||||
|
|
ния |
которых |
задаются |
для |
||||
|
|
|
|||||||
|
|
|
начального |
момента времени. |
|||||
|
|
|
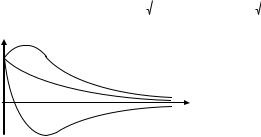
Возможные варианты графиков |
||||||
0 |
t |
изменения x со временем t изоб- |
|||||||
|
|
|
ражены на рис. 2.3. |
|
|||||
Рис. 2.3 |
|
|
Условие 0 , когда колеба- |
||||||
|
|
тельная система |
быстрее |
всего |
|||||
|
|
|
|||||||
приходит в положение равновесия, называется демпфированием. Примеры демпфирования – движение мягко закрывающейся двери, снабжённой демпферным тормозом-доводчиком, работа
амортизаторов автомобиля и т. д.
2.2 Вынужденные колебания
Реальный колебательный процесс сопровождается потерями энергии, поэтому для его поддержания система должна периодически получать энергию извне, компенсирующую потери. Коле-
бания, происходящие под действием внешней периодически действующей силы, называются вынужденными.
В случае механических колебаний учёт действия этой силы сводится к добавке соответствующего слагаемого в формулу второго закона Ньютона; для описания процессов в электрическом колебательном контуре дополнительное слагаемое, соответствующее включению в контур источника с переменной э.д.с., вводится в формулу закона Ома (для неоднородного участка цепи).
Поскольку, как мы уже убедились, вид соответствующих дифференциальных уравнений (и их решений) одинаков для самых разных колебательных систем, далее мы будем рассматривать
13
процессы, происходящие лишь в одной из них: в электрическом колебательном контуре.
Рассмотрим контур, в который кроме конденсатора с электро-
|
|
|
1 |
|
2 |
|
|
|
ёмкостью C, катушки с индуктивностью |
|||||||||||||||||||
|
|
|
|
|
|
|
L |
|
и |
|
|
резистора |
с |
сопротивлением R |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
C |
|
K |
|
|
|
|
|
|
|||||||||||||||||
R |
|
|
|
|
|
|
включён |
|
источник |
переменной |
э.д.с., |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
E E0cos t |
|
|||||||||||||||||||||||
|
|
меняющейся по косинусоидальному за- |
||||||||||||||||||||||||||
|
|
|
|
L |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
кону E E0cos t (здесь E0 – амплитуд- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
EСИ |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
ное значение э.д.с., – частота). Схема |
||||||||||||||||||||||
|
|
|
Рис. 2.4 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
контура приведена на рис. 2.4. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Формула закона Ома теперь имеет вид: |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
IR 2 1 EСИ E0cos t, |
|
||||||||||||||||||
а с учётом того, что EСИ |
|
|
|
, |
I |
|
|
|
|
|
|
2) |
||||||||||||||||
L I |
q , |
|
I |
q , С q/( 1 |
||||||||||||||||||||||||
q/ U, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
E0cos t. |
(2.9) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
q R |
C |
L q |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Приведём данное дифференциальное уравнение к канониче- |
|||||||||||||||||||||||||||
скому виду: q |
|
R |
q |
|
|
1 |
|
|
q |
|
E0 |
cos t, а затем, вновь введя |
||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
LC |
|
|
|
|
|
L |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
обозначения |
R |
, 0 |
|
1 |
|
|
, запишем окончательно: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2L |
|
|
|
|
|
|
LC |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
E0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
q |
|
|
|
cos t. |
(2.10) |
||||||||||||
|
|
|
|
|
|
|
|
|
q 2 q |
|
|
|
||||||||||||||||
L
Данное уравнение относится к неоднородным (в его правой части стоит не ноль, а некоторое выражение). В теории дифференциальных уравнений показано, что общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения данного неоднородного уравнения. В нашем случае это означает, что решение уравнения (2.10) при 0 можно представить следующим образом:
q A0e t cos( t ) q0cos( t ), |
(2.11) |
14

где q0 |
|
|
E0 |
|
, tg |
2 |
. |
|||
|
|
|
|
|
2 |
2 |
||||
L ( 2 |
2 ) 2 |
4 2 2 |
0 |
|||||||
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|||
Первое слагаемое в формуле (2.11) описывает затухающие колебания в контуре, которые со временем прекращаются. Таким образом, после краткого переходного периода первое слагаемое станет практически равным нулю, и заряд на конденсаторе будет изменяться по гармоническому закону
q q0cos( t ), |
(2.12) |
однако колебания теперь будут вынужденными, происходящими с частотой внешней вынуждающей (электродвижущей) силы.
Существенно, что амплитуда q0 этих колебаний зависит от частоты этой силы, а это означает, что при некотором значении функция q0( ) может иметь максимум, то есть колебания окажутся особенно сильными.
Контрольные задания и вопросы
1.На примере пружинного маятника запишите дифференциальное уравнение затухающих колебаний и его решение.
2.На примере электрического колебательного контура запишите дифференциальное уравнение затухающих колебаний и его решение.
3.Проведите аналогию между механическими и электрическими колебательными процессами.
4.Дайте определения основным параметрам, характеризующим затухающие колебания: коэффициенту затухания, декременту затухания, логарифмическому декременту затухания, добротности.
5.Что называется демпфированием? Какое условие должно выполняться для демпфирования?
6.Какой процесс называется апериодическим, и каково условие его возникновения?
7.На примере электрического колебательного контура объясните, как возникают затухающие колебания. Запишите уравнение этих колебаний.
15
Лекция № 3 |
КОЛЕБАНИЯ. ЧАСТЬ III |
3.1 Явление резонанса
Резонансом называется явление резкого возрастания амплитуды колебаний под действием внешнего периодической силы.
Резонанс по напряжению в колебательном контуре наблюдается, когда амплитуда U0 напряжения на обкладках конденсатора принимает максимальное значение,
U0 |
q0 |
|
|
|
|
E0 |
|
|
|
|
|
|
U0( ). (3.1) |
|
C |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
LC ( 0 |
2 |
|
) |
2 |
4 |
|
2 |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
||||
Очевидно: максимум функции U0( ) достигается в случае, когда подкоренное выражение y ( 02 2)2 4 2 2 минимально. Для получения условия данного экстремума введём обозначение2 z, найдём производную yz 2( 02 z) 4 2, после чего приравняем её нулю: 2( 02 z) 4 2 0. Экстремум имеет место при z 02 2 2, то есть резонанс по напряжению достигается при частоте переменной вынуждающей силы (в нашем случае –
электродвижущей), равной
U0( )
|
1 0 |
|
2 1 |
E0 |
3 2 |
0 |
|
|
РЕЗ1 0 |
РЕЗ2 
 02 2 2 0РЕЗ3
02 2 2 0РЕЗ3 
 02 2 2 РЕЗ2 0
02 2 2 РЕЗ2 0
|
|
|
|
|
|
2 |
2 2 . |
(3.2) |
|
|
0 |
|
|
|
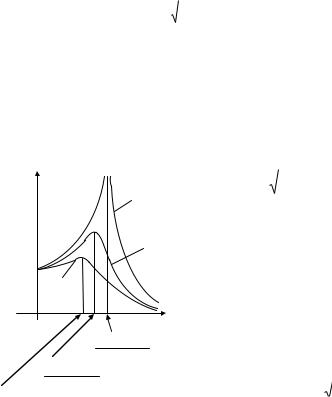
Графики зависимости амплитуды U0( ) напряжения на конденсаторе от частоты внешней вынуждающей силы представлены на рис. 3.1.
Отметим:
- чем меньше , тем больше амплитуда колебаний (при 0 U0( ) ), кроме того, при 0
РЕЗ 0 |
|
1 |
|
; |
|
|
|
||
|
|
|
||
|
||||
|
|
LC |
||
Рис. 3.1
- чем меньше , тем больше ча-
стота , при которой наблюдается резонанс (при 0 частота РЕЗ1 0);
16

- при частоте 0 колебаний в системе не происходит, напряжение на конденсаторе постоянно и равно E0;
- при резонансе |
2 2 2 и, |
|
подставив это значение в |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
формулу |
(3.1), |
получим, что |
при |
|
резонансе U0 U0макс |
|||||||||||||
|
|
E0 |
|
|
|
. Учитывая, что 0 |
|
|
|
1 |
|
, для 0 можно запи- |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
LC |
|
|
||
|
2 LC |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сать: |
U 0 макс |
|
|
0 |
Q, где, согласно формуле (2.7), Q – доброт- |
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
E0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
ность контура. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Резонанс по току в колебательном контуре наблюдается, когда максимального значения достигает амплитуда I0 силы тока в цепи:
I |
d[q0cos( t - )] |
q0 sin( t ) I0cos( t |
|
|
), где |
|||||||||||
dt |
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
I0 I0( ) |
|
|
|
|
E0 |
|
|
|
|
|
E0 |
|
|
. |
(3.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
L ( 2 |
|
|
|
|
|
|
||||||||||
|
|
2 ) 2 4 2 2 |
|
|
|
|
( 2 |
2 ) 2 |
|
|
|
|
||||
|
0 |
|
|
|
|
|
L |
0 |
|
4 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимум функции I0 ( ) достигается в случае, когда подкоренное выражение минимально, то есть – когда минимально первое слагаемое. Но оно всегда положительно, и его минимальное
I0( ) |
|
значение может быть только нулём. |
|
Так мы получаем условие резонанса |
|
1 |
0 |
по току: |
|
|
2 1
|
3 2 |
0 РЕЗ1 0 |
|
Рис. 3.2 |
|
0. |
(3.4) |
Графики зависимости амплитуды I0( ) силы тока в контуре от частоты возбуждающей э.д.с. представлены на рис. 3.2.
Отметим:
- чем меньше , тем больше амплитуда колебаний (при 0 I0( ) ),
17
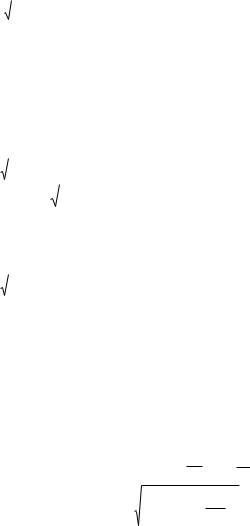
-резонансная частота РЕЗ1 не зависит от коэффициента затухания ;
-при частоте 0 колебаний в системе не происходит, сила тока в цепи равна нулю;
- при резонансе I0макс |
|
E0 |
|
E0 |
. |
|
|
|
|
|
|||
|
L |
|
4 2 |
|
R |
|
Примечание 1
Очевидно, что в случае механических колебаний формулы (3.1) и (3.2) соответствуют условиям резонанса «по координате». Так, для амплитуды A колеблющегося под действием переменной силы F F0cos t пружинного маятника массой m можно записать:
A |
|
|
|
F0 |
|
|
|
. |
(3.5) |
||
|
|
|
|
|
|
|
|
||||
|
m ( 2 |
2 )2 |
4 2 2 |
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
r |
. |
|||
Резонанс достигается при |
|
|
2 |
22 |
, где |
||||||
|
|
|
|||||||||
|
|
|
|
0 |
|
|
|
2m |
|||
|
|
|
|
|
|
|
|
|
|
||
Условия (3.3) и (3.4) соответствуют резонансу «по скорости» ( x ), в частности:
0 |
|
|
F0 |
|
|
, |
(3.6) |
|
|
|
|
|
|
||||
m ( 2 |
2 )2 4 2 2 |
|||||||
|
|
|
|
|||||
0 |
|
|
|
|
|
|||
и резонанс происходит при 0.
Примечание 2
Отметим некоторые особенности цепи переменного тока, которой является колебательный контур, содержащий последовательно соединённые конденсатор с электроёмкостью C, катушку с индуктивностью L, резистор с сопротивлением R и источник переменной э.д.с. (с частотой ).
1. Используя закон Ома, уравнение (3.3) и то, что 02 1 , R ,
LC 2L
запишем для полного сопротивления цепи: Z |
R |
2 |
|
|
L |
||
|
|
|
|
2
1 .C
18
Если R 0, |
L 0, то Z |
XC |
1 |
– реактивное емкостное |
||
|
||||||
C |
||||||
|
|
|
|
|
||
сопротивление (при 0 |
XC ). |
|
|
|||
Если R 0, |
C , то |
Z XL L – реактивное индуктив- |
||||
ное сопротивление (при 0 |
XL 0). |
|
||||
Разность XL XC L |
1 |
– реактивное сопротивление кон- |
||||
C |
||||||
|
|
|
|
|
||
тура. |
|
|
|
|
|
|
2. Напряжение на активном сопротивлении (резисторе) меняется |
||||||
в фазе с током: UR |
IR RI0cos( t ) URмаксcos( t |
). |
|||||||
|
|
|
|
2 |
2 |
||||
Напряжение на конденсаторе отстаёт по фазе от силы тока на : |
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
UС |
q |
|
q0 |
cos( t ) UСмаксcos( t ). |
|
||
|
|
|
|||||||
|
|
|
C |
|
C |
|
|||
Напряжение на катушке индуктивности на опережает по фазе |
|||||||||
|
|
|
|
2 |
|
||||
ток: |
|
|
|
|
|
|
|||
UL L |
dI |
I0 Lsin( t |
|
) I0 Lcos( t ) ULмаксcos( t ). |
|||||
|
|
||||||||
|
dt |
2 |
|
|
|||||
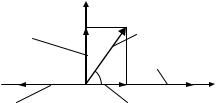
3. Связь между значениями напряжения на элементах колебательного контура может быть отображена с помощью векторной диаграммы (рис. 3.3).
В момент времени t1 когда t1 |
0, U1 |
ZI1 Uмаксcos t1. |
|||||||||
UR |
|
|
|
|
Из рисунка, в частно- |
||||||
|
|
|
|
сти, следует, что |
|
|
|
||||
|
|
|
|
|
|
|
|
||||
URмакс RIмакс |
|
Uмакс ZIмакс |
|
|
tg |
U |
RMAKC |
|
|
R |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
UCMAKC ULMAKC |
|
1 |
L |
|
||
|
|
UCмакс Iмакс |
|
|
|
C |
|
|
|||
|
C |
|
|
|
|
|
|
||||
0 |
|
U |
|
|
что |
соответствует |
фор- |
||||
ULмакс L Iмакс |
UCмакс ULмакс |
|
|
муле (2.11). |
|
|
|
|
|||
Рис. 3.3
19
