
Lektsii_Fizika_chast_II
.pdf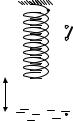
3.2Автоколебания
Вавтоколебательных системах колебательные движения возникают и поддерживаются за счёт постоянного, не меняющего свои параметры со временем источника энер-
|
|
|
|
|
|
|
|
|
|
|
гии. Колебательная система сама управляет |
|
|
|
|
|
|
|
|
|
|
|
|
П |
|
|
|
|
K |
внешним воздействием, периодический харак- |
|||||
|
|
|
|
|
|
|
|
|
|
E |
тер носит процесс управления. |
|
|
|
|
|
|
|
|
|
|
Пример подобной системы дан на рис. 3.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
Металлический груз Г подвешивают на про- |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
водящей пружине П так, чтобы он касался по- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Э |
|
|
|
|
|
верхности проводящей жидкости – электролита |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Э (например, подсоленной воды). К системе |
Рис. 3.4 |
подключают источник постоянной э.д.с. E: один |
|
из электродов погружается в электролит, другой подсоединяется к пружине. При замыкании ключа K в цепи возникает электрический ток, витки пружины (по ним токи идут в одну сторону) начинают притягиваться друг к другу: груз поднимается, перестаёт касаться электролита, и цепь разрывается. Разрыв цепи означает исчезновение тока, витки перестают притягиваться, но тогда груз снова опускается в электролит: цепь восстанавливается и в ней вновь возникает электрический ток. Процесс носит периодический характер, колебаниями груза управляет сама система.
Контрольные задания и вопросы
1.Что называется резонансом? Приведите примеры.
2.Начертите графики резонанса по напряжению и резонанса по току. Что общего между графиками и в чём состоит отличие?
3.Сравните резонансные кривые механических и электрических колебательных систем.
4.Запишите выражение для полного электрического сопротивления колебательного контура и продемонстрируйте, что оно действительно измеряется в омах.
5.Постройте векторные диаграммы, поясняющие процессы, протекающие в колебательном контуре.
6.Что называется автоколебаниями? Приведите примеры.
20
Лекция № 4 КОЛЕБАНИЯ. ЧАСТЬ IV
4.1 Сложение колебаний, происходящих в одном направлении
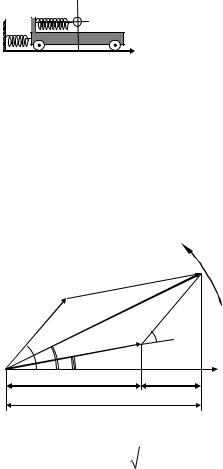
Рассмотрим ситуацию, когда тело одновременно участвует в двух гармонических колебаниях, происходящих вдоль оси X (при-  мер – шарик на тележке, рис. 4.1), одно
мер – шарик на тележке, рис. 4.1), одно 
 (шарика относительно тележки) описы-
(шарика относительно тележки) описы-
вается уравнением x1 A1cos( 1t 1), а второе (тележки относительно земли) –
0 |
X |
уравнением x2 |
A2cos( 2t 2). Резуль- |
Рис. 4.1 |
|
||
|
тирующее движение шарика относи- |
||
|
|
||
тельно земли будет периодическим, но в общем случае соответствующую формулу временнòй зависимости смещения шарика от положения равновесия x(t) записать не так легко. Однако можно выделить несколько частных случаев, когда результат сложения колебаний представляется достаточно просто.
a) Сложение колебаний одинаковой частоты ( 1 2 ):
x1 A1cos( t 1),
t 0
A2 |
|
A |
|
|
|
|
|
2 |
1 |
2 |
|
A1 |
||
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
|
|
|
x |
|
|
Рис. 4.2
x2 A2cos( t 2).
Результат сложения этих
колебаний – также гармоническое колебание, происходящее с той же частотой , амплитудой A и начальной фазой :
x x1 x2 Acos( t ).
X Значения A и можно получить, пользуясь методом векторных диаграмм (см. рис. 4.2). Из рисунка следует:
|
|
|
|
|
|
|
|
|
|
|
|
A A |
2 |
A 2 |
2A A cos( |
2 |
) , |
(4.1) |
|||||
1 |
2 |
1 |
2 |
|
1 |
|
|
||||
tg |
|
A1sin 1 |
A2sin 2 |
. |
|
|
|
(4.2) |
|||
|
|
|
|
|
|
|
|||||
|
|
|
A1cos 1 |
A2cos 2 |
|
|
|
|
|||
21
Если 2 1 2 m (здесь m – целое неотрицательное число), то амплитуды колебаний складываются: A A1 A2 (колебания
синфазны).
Если 2 1 (2m 1) , амплитуды вычитаются: A |A1 A2| (колебания совершаются в противофазе). В частном случае при A1 A2 тело покоится, A 0.
b) Сложение колебаний с сильно различающимися частотами
( 1 2)
Результат сложения таких колебаний поясняется рисунком 4.3. В подобных случаях говорят о том, что колебание с частотой
2 модулировано колебанием с частотой 1. x Результирующий процесс x(t)
0  t
t
x1 A1cos(1t 1) |
x2 A2cos(2t 2) |
Рис. 4.3
c) Сложение колебаний с близкими частотами ( 1 2). Биения
Пусть складываются два колебания вида
x1 Acos( t), и |
x2 Acos[( )t)], |
где . Для простоты считаем, что амплитуды колебаний одинаковы, и начальные фазы равны нулю.
Тогда для результирующего процесса можно записать:
x x1 |
x2 |
Acos( t) Acos[( )t)] 2Acos |
|
t cos[( |
|
|
)t], |
||
|
2 |
|
|||||||
|
|
2 |
|
|
|
|
|||
или, поскольку и, тем более, /2, получаем: |
|
, |
|||||||
|
|
|
|||||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
||
22
x 2Acos t cos( t) A*(t) cos( t). |
(4.3) |
2 |
|
Таким образом, результат сложения гармонических колебаний, происходящих в одном направлении с близкими частотами, можно рассматривать, как гармоническое же колебание, амплитуда которого сама меняется со временем по закону косинуса (синуса): см. рис. 4.4. Данный процесс называется биениями.
x |
Биения x(t) A*(t) sin(t) |
2A |
|
0  t
t
2A
A*(t) 2Acos t
2
Рис. 4.4
4.2Сложение взаимно перпендикулярных колебаний
4.2.1Сложение взаимно перпендикулярных колебаний с равными частотами
|
|
Рассмотрим ситуацию, когда тело |
||||
|
|
одновременно участвует в двух гар- |
||||
|
|
монических колебаниях, одно из ко- |
||||
0 |
X |
торых происходит вдоль оси X, а дру- |
||||
гое вдоль оси Y (пример – шарик на |
||||||
|
|
|||||
|
|
тележке, |
вид |
сверху |
показан на |
|
Y |
|
рис. 4.5). |
Одно |
колебание (шарика |
||
|
относительно тележки) |
описывается |
||||
|
|
|||||
Рис. 4.5 |
|
уравнением x Acos( t 1), а второе |
||||
|
(тележки относительно земли) – урав- |
|||||
|
|
|||||
нением y Bcos( t 2).
Результирующее движение шарика относительно земли будет периодическим, но в общем случае соответствующая формула
23

временнòй зависимости смещения шарика от положения равновесия x(t) записать не так просто. Однако можно выделить несколько частных случаев, когда результат сложения колебаний представляется достаточно легко.
a)Разность начальных фаз колебаний 2 1 2 m (m – целое
число)
xAcos( t 1),
yBcos( t 2), причём (по условию) 2 1 2 m. Это означает: y Bcos( t 1 2 m) Bcos( t 1), или
y |
B |
x. |
(4.4) |
|
|||
|
A |
|
|
|
|
|
|
Формула показывает: траектория шарика является отрезком прямой линии; координата x меняется в пределах от A до A, а координата y – в пределах от B до B. (см. рис. 4.6а).
b)Разность начальных фаз колебаний 2 1 (2m 1)
xAcos( t 1),
yBcos( t 2) Bcos( t 1 2 m) Bcos( t 1), или
y |
B |
x. |
(4.5) |
|
|||
|
A |
|
|
|
|
|
|
Траекторией шарика и в этом случае является отрезок прямой линии, однако в системе координат XY он проходит не через первый и третий, а через второй и четвёртый квадранты (рис. 4.6б).
|
Y |
|
Y |
|
||
|
B |
|
B |
|
||
A |
|
0 A X |
A 0 |
A X |
||
|
|
|
|
|
|
|
|
B |
B |
|
|||
|
а) |
|
б) |
|
||
|
|
|
Рис. 4.6 |
|
||
24
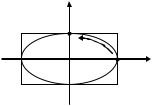
c) Разность начальных фаз колебаний 2 |
1 (2m 1) |
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
x Aсos( t 1) |
или cos( t 1) |
x |
, а |
cos2( t 1) |
x2 |
, |
||||
|
A2 |
|||||||||
|
|
|
|
A |
|
|
|
|
||
y Bcos( t 2) Bcos( t 1 |
) Bsin( t 1), |
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
или sin( t 1) |
y |
, а |
sin2( t 1) |
y2 |
. |
|
||||
|
|
|
||||||||
|
|
B |
|
|
|
B2 |
|
|||
Поскольку sin2( t 1) cos2( t 1) 1, уравнение траектории шарика приобретает вид:
|
Y |
|
|
|
|
|
x2 |
|
y2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1. |
(4.6) |
|||||
|
B 2 |
|
|
|
|
|
A2 |
|
B2 |
||||||||
|
|
|
|
1 |
|
|
|
Это – каноническое уравнение эллип- |
|||||||||
A |
0 |
|
|
A X |
|
са (при A B – окружности), рис. 4.7. |
|||||||||||
|
B |
|
|
|
|
Если 1 0, 2 |
, то x Acos( t), y |
||||||||||
|
Рис. 4.7 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
Bsin( t). В момент времени t 0 x A, |
||||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y 0 (точка 1 на рис 4.7). Через четверть |
|||||||||||
периода (t |
T |
, где T |
2 |
) |
x Acos( |
1 |
|
2 |
) Acos |
0, зато |
|||||||
|
4 |
|
|
|
4 |
|
|
2 |
|
||||||||
y Bsin( ) B (точка 2 на рис. 4.7), то есть движение шарика
2
происходит против часовой стрелки (от точки 1 к точке 2 и далее).
Аналогично можно показать, что при 2 1 |
|
движение |
|
2 |
|
осуществляется в направлении по часовой стрелке.
Примечание 1
Если 2 1 m, траекторией является эллипс, оси
2
которого повёрнуты относительно осей X и Y на некоторый угол. Каноническое уравнение такого эллипса имеет вид:
x2 |
|
y2 |
|
2xycos( |
sin2( ). |
(4.6) |
A2 |
B2 |
|
||||
|
|
AB |
|
|||
25

Примечание 2
Если частоты колебаний неодинаковы, но близки ( 2 1 ), уравнения колебаний можно записать в виде
xAcos( 1t 1),
yBcos( 2t 2) Bcos( 1t 2 t) Bcos[ 1t 2*(t)].
Вэтом случае разность 2* 1 оказывается зависящей от
времени и принимает все возможные значения, а траектория движения непрерывно меняется, превращаясь то в отрезок, то – в эллипс и обратно. Данный процесс удобно наблюдать на экране осциллографа, подавая на пластины, отклоняющие электронный луч по вертикали и горизонтали напряжение с близкими частотами.
4.2.2 Сложение взаимно перпендикулярных колебаний с кратными частотами
В этом случае траекторией будет замкнутая линия, число са-
мопересечений которой зависит от отношения частот 1 : 2. Соответствующие кри-
0 |
|
|
|
|
|
3 |
|
вые называются фи- |
|||
|
|
|
|||||||||
|
4 |
2 |
|
4 |
|
гурами |
Лиссажу. |
||||
|
|
|
|
|
|
|
|
||||
1 : 2 1 1 |
|
|
|
|
|
|
|
Реальный вид фигур |
|||
|
|
|
|
|
|
|
зависит |
от |
соотно- |
||
|
|
|
|
|
|
|
|
||||
1 : 2 1 2 |
|
|
|
|
|
|
|
шения |
амплитуд, |
||
|
|
|
|
|
|
|
частот |
и |
разности |
||
|
|
|
|
|
|
|
|
||||
1 : 2 1 3 |
|
|
|
|
|
|
|
фаз |
складываемых |
||
|
|
|
|
|
|
|
колебаний. |
Приме- |
|||
|
|
|
|
|
|
|
|
||||
1 : 2 2 3 |
|
|
|
|
|
|
|
ры |
некоторых из |
||
|
|
|
|
|
|
|
таких фигур приве- |
||||
|
|
|
|
|
|
|
|
||||
1 : 2 3 4 |
|
|
|
|
|
|
|
дены на рис. 4.8. |
|||
|
|
|
|
|
|
|
Если |
отношение |
|||
|
|
|
|
|
|
|
|
частот |
не |
является |
|
|
|
|
Рис. 4.8 |
|
|
целым |
|
числом, |
|||
|
|
|
|
|
|
|
|
форма фигур непре- |
|||
рывно меняется. Этот процесс соответствует изменению со временем разности фаз (t) 2* 1.
26

|
|
|
|
|
Примечание 3 |
|
|
|
|
|
|
|
|
|
|
||||
В заключение раздела «Колебания» напомним основные соот- |
|||||||||||||||||||
ношения, используемые при решении задач по данной теме. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
КОЛЕБАНИЯ |
|
|
|
|
|
|
|
|
|
|
||
МЕХАНИЧЕСКИЕ |
|
|
|
|
|
|
ЭЛЕКТРИЧЕСКИЕ |
|
|
|
|
|
|||||||
дифференциальное |
x 2 |
r |
|
x |
k x 0 |
дифференциальное |
|
|
R |
q |
|
1 |
q 0 |
||||||
|
2m |
m |
|
|
q 2 |
|
|
|
|||||||||||
уравнение |
|
|
|
|
уравнение |
|
|
|
2L |
|
LC |
|
|||||||
|
|
|
|
|
2 |
|
|
или |
q 2 q |
2q 0 |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
или x |
2 x 0 |
x 0 |
|
|
|
|
|
|
|
|
0 |
|
||||||
смещение |
|
|
|
x |
|
|
|
|
заряд |
|
|
|
|
q |
|
|
|
|
|
масса |
|
|
m |
|
|
|
|
индуктивность |
|
|
|
|
L |
|
|
|
|
||
коэффициент |
|
|
|
r |
|
|
|
|
электрическое |
|
|
|
|
R |
|
|
|
|
|
сопротивления |
|
|
|
|
|
|
|
сопротивление |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
коэффициент |
|
|
|
k |
|
|
|
|
величина, обратная |
|
|
|
1/C |
|
|
|
|||
жёсткости |
|
|
|
|
|
|
|
электроёмкости |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
коэффициент затухания |
|
r/(2m) |
|
|
коэффициент затухания |
|
|
R/(2L) |
|
||||||||||
скорость |
|
x |
|
|
|
сила тока |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
I q |
|
|
|
||||||||
потенциальная |
WП kx 2 |
|
|
энергия электрическо- |
|
|
WЭ |
|
q2 |
|
|
||||||||
энергия |
|
|
|
|
2 |
|
|
|
го поля конденсатора |
|
|
|
|
2C |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
кинетическая |
WК m |
2 |
|
|
энергия магнитного |
|
|
WМ LΙ |
2 |
|
|||||||||
|
|
|
поля катушки |
|
|
|
|
|
|
||||||||||
энергия |
|
|
|
|
2 |
|
|
|
индуктивности |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Собственная частота |
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
пружинного |
0 |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
маятника |
|
|
|
|
|
Собственная частота |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
математического |
|
|
|
|
g |
|
|
|
электрического |
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
колебательного |
|
|
|
0 |
|
|
|
|
|
||||
маятника |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
l |
|
|
|
контура |
|
|
|
|
|
|
LC |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
физического |
0 |
|
|
mgd |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
маятника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
циклическая частота |
|
k |
|
|
r |
|
2 |
циклическая частота |
|
|
|
1 |
|
|
|
R |
2 |
||
затухающих колебаний |
|
|
|
затухающих колеба- |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
пружинного маятника |
|
m |
|
2m |
|
ний |
|
|
|
LC |
|
2L |
|
||||||
логарифмический |
|
|
|
|
|
|
|
|
T 2 / 0 |
|
|
|
|
|
|
|
|
|
|
декремент затухания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
добротность |
Q 2 |
|
|
|
W |
; |
при малых |
Q |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
W (t) W (t T ) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
Контрольные задания и вопросы
1.Рассмотрите сложение колебаний одинаковой частоты и одного направления. Получите выражения для расчёта амплитуды
ифазы результирующего колебания.
2.Что называется биениями?
3.Рассмотрите сложение взаимно перпендикулярных колебаний с равными частотами и следующими значениями разности
фаз: 2 m, (2m 1) , (2m 1) . Получите уравнения траектории
2
итогового движения колеблющейся точки.
4.Что называется фигурами Лиссажу?
5.Проведите сопоставление параметров, характеризующих механические и электрические колебания.
28
Лекция № 5 |
ВОЛНЫ. ЧАСТЬ I |
5.1 Определения
Волной называется процесс распространения колебаний в пространстве. Если волна распространяется в упругой среде, она называется упругой волной.
Волны, распространяющиеся в неограниченной среде, называются бегущими. Основное свойство таких волн – перенос энергии без переноса вещества.
Если колебания совершаются вдоль направления распространения волны, такие волны называются продольными (пример: звуковые волны в газах).
Если колебания совершаются в направлении, перпендикулярном направлению распространения волны, такие волны назы-
ваются поперечными (примеры: волны на поверхности воды, электромагнитные волны, в частности – свет).
При распространении волны в каждый момент времени можно мысленно выбрать поверхность, отделяющую часть пространства, в которой уже происходят колебания, от той части, где их ещё нет. Эта поверхность называется фронтом волны.
Если фронт волны – плоскость, волна называется плоской, ес-
ли сфера – сферической.
Фронт волны непрерывно движется. Скорость движения фронта называется скоростью волны (фазовой скоростью).
Расстояние, которое фронт проходит за время одного колебания (рис. 5.1), называется длиной волны :
T или / , |
(5.1) |
где – скорость волны, T – период колебаний, – частота колебаний.
Очевидно: длина волны – это расстояние между соседними ча-
стицами упругой среды, колеблющимися в одной фазе.
Геометрическое место точек, колеблющихся в одной фазе,
называется волновой поверхностью.
29
