3.3.3 Построение простых планов контроля с заданными свойствами

Ранее было показано, что применению однократного плана контроля по качественному признаку соответствует проверка параметрической гипотезы типа

При этом накопленное число дефектных изделий в выборке выступает в роли контролируемой величины, и критическая область имеет вид. С помощью оперативной характеристикиили других параметров плана можно охарактеризовать полностью или приблизительно критерий проверки гипотезы:

партия отвечает требованиям к качеству;

партия не отвечает требованиям к качеству.

В настоящем разделе ставится обратная задача, и исследуется вопрос о том, как должен выглядеть план контроля, чтобы его оперативная характеристика имела заданные свойства. Поскольку однократный план при объеме партии (который можно считать заданным) описывается, как и раньше, посредством параметрови, то для их определения необходимо знать две величины, с помощью которых можно вывести выражения дляи. Определить параметры можно с помощью следующих данных:

• координат двух точек 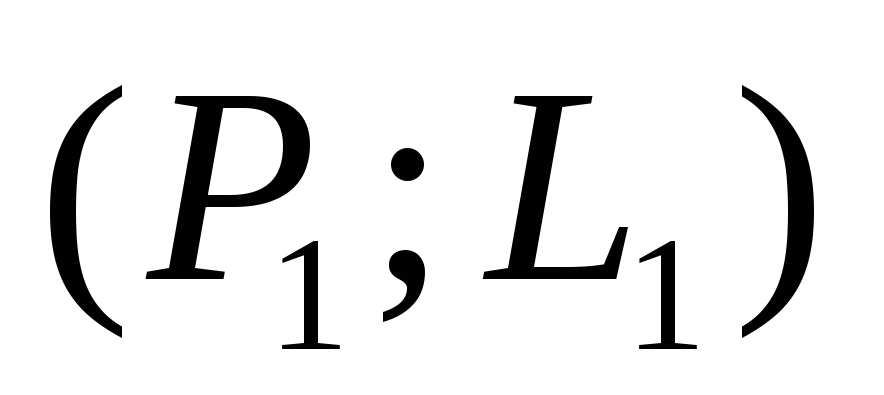и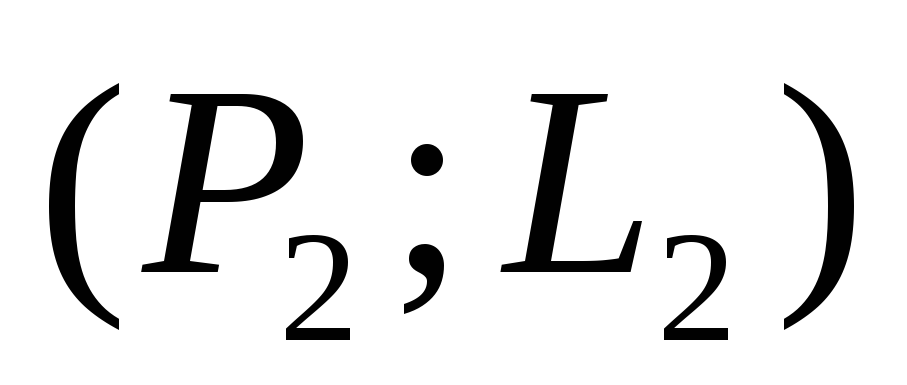, которые должны лежать на оперативной характеристике;

• координат одной точки 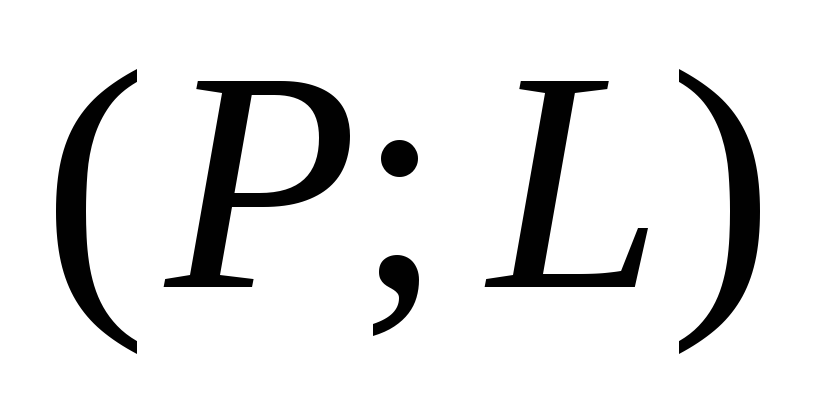оперативной характеристики и крутизны или чувствительности в этой точке;

• координат одной точк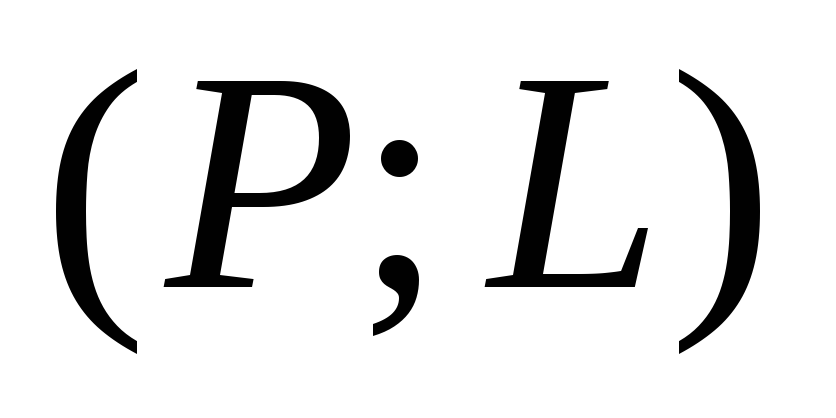и оперативной характеристики и значения среднего выходного уровня дефектности. Внутри группы планов контроля, соответствующих этим данным, выбирается план с минимальным числом проконтролированных изделий.

Остановимся подробно на первых двух возможностях построения плана контроля.

3.3.3.1 Задание риска потребителя и риска поставщика

Наиболее распространенный метод построения однократных планов контроля связан с заданием уровней дефектности ии соответствующих рисков производителяи поставщика. Оперативная характеристика искомого плана должна проходить через обе точкии, то есть должно выполнятьсяи. Из-за целочисленности обоих параметровиэти требования, как правило, выполняются лишь приближенно

, (3.111а)

(3.111б)

с и. Чтобы заданные рискиине были превышены, нужно выполнение условияи, то есть

, (3.112а)

. (3.112б)

Выполнение (3.112) означает, что параметры плана контроля иопределяются так, что значения рисков, то есть действительного риска производителяи действительного риска поставщика, по крайней мере, не превышают пред­писанного риска производителяи предписанного риска потребителя.

Зависимости (3.111) означают, что квантили оперативной характеристики иявляются квантилями оперативной характеристики порядкаи.

, (3.113а)

. (3.113б)

Обозначим заданные значения какпредписанные квантили оперативной характеристики. Относящиеся к предписанному риску и предписанному рискуквантили

, (3.114а)

(3.114б)

называются действительными квантилями оперативной характеристики.

В силу (3.112) для названных квантилей выполняются условия

, (3.115а)

. (3.115б)

Графическая иллюстрация полученных соотношений приведена на рис.3.29.

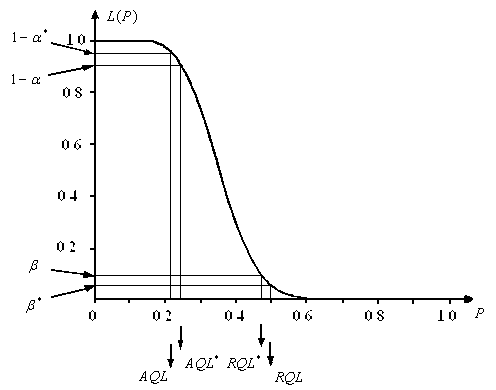
Рис.3.29 Предписанные и действительные квантили и предписанный и действительный риски для плана контроля по качественному признаку

Однократный план контроля по качественному признаку, удовлетворяющий неравенству (3.112) или эквивалентному ему неравенству (3.115), называют допустимым планом контроля. Ранее отмечалось, что путем выбора достаточно большого при постоянномможно всегда добиться того, чтобы оперативная характеристика однократного плана контроляв точкеотвечала условию. С увеличениемпри постоянномфункциюв точкеможно сделать большей, чем.

Какой из допустимых планов следует выбрать? По экономическим соображениям выбирают план, при котором выполняется неравенство (3.112) с минимальным . Из всего количества парцелых чисел, гдеи, выбирают ту пару, в которойминимально. Определитьипри дискретных распределениях (гипергеометрическом, биномиальном, распределении Пуассона) невозможно аналитически, можно использовать только численно - итеративные методы (рис.3.30).

Основная идея алгоритма заключается в следующем: начинают с приемочного числа и объема выборкии вычисляют для выбранного распределения (гипергеометрического, биномиального или распределения Пуассона) значения оперативной характеристикив точке, с тем, чтобы проверить условие. Объем выборкипри постоянномво внутреннем цикле увеличивается на единицу до тех пор, пока не будет выполнено условие. Потом с найденнымиивычисляют значение функциив точке, и проверяют условие.

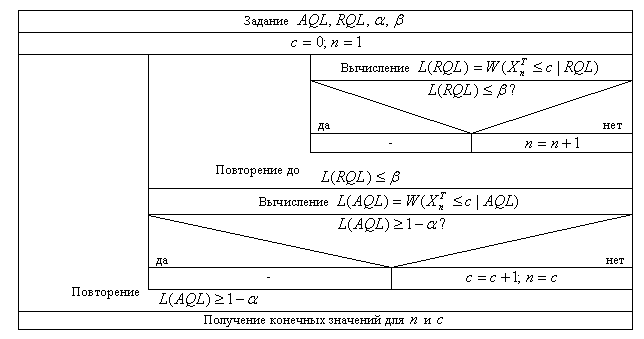
Рис.3.30 Структурограмма поискового алгоритма

Если это условие выполняется, то это означает, что найден минимальный по объему план контроля. В противном случае величину во внешнем цикле увеличивают на единицу, подставляюти снова входят во внутренний цикл. По­лученный таким способом минимальный по объему план имеет наибольшее отклонениеот предписанного риска изготовителя и наименьшее отклонениеот предписанного риска поставщика.

Применение изображенного на рис.3.30 алгоритма не связано с определенной гипотезой относительно распределения контрольной величины . Если алгоритм хотят применить на практике, то для определенияинужно исходить из конкретного распределения. Для вычислений требуется достаточно подробная таблица распределений или соответствующее программное обеспечение для проведения вычислений на компьютере. Если использовать действительно имеющее место трехпараметрическое гипергеометрическое распределение, то вышеназванные предпосылки для вычисленияичасто не выполняются. Если дляпринять биномиальное распределение или распределение Пуассона, то ситуация будет более благоприятной. Неравенства (3.112) вбиномиальном случае можно записать в виде:

, (3.116а)

, (3.116б)

а в случае распределения Пуассона как:

, (3.117а)

, (3.117б)

так что для применения данного алгоритма необходимо знание только опреде­ленных значений функции распределения Фишера (распределения) илираспределения. Поскольку системы неравенств (3.112) и (3.115) эквивален­тны, то неравенства (3.116) и (3.117) можно выразить через соответствующие квантили. При использованиибиномиального распределения получим:

, (3.118а)

, (3.118б)

а в случае распределения Пуассона:

, (3.119а)

. (3.119б)

На использовании неравенств (3.119), которые можно представить в виде цепочки

, (3.120)

основывается способ для определения параметров ипри использовании распределения Пуассона. Согласно этому способу в неравенства подставляют последовательно значенияи сравнивают значенияииз (3.120), применяя таблицыквантилей. То значениеявляется приемочным числом искомого плана, начиная с которого выполняется. Если полученное таким образом значение подставить в (3.120), то каждое натуральное число, при котором (3.120) выполняется, является объемом выборки допустимого плана. Значение, которое нужно выбрать – это наименьшее из всех значений.

Если допустимый план с минимальным объемом выборки получен с помощью приближения Пуассона, то возникает вопрос, отвечает ли определенная через значения иоперативная характеристика Пуассона соответствующей гипергеометрической оперативной характеристики с тем же самым риском производителя и поставщика, или точнее, выполняются ли для полученных результатовиприитакже и неравенстваи. Поскольку гипергеометрическая оперативная характеристикаочень сложна в обращении, но через биномиальную оперативную характеристикуаппроксимируется лучше, чем через оперативную характеристику Пуассона, то на практике часто ограничиваются проверкой того, в достаточной ли степени найденная оперативная характеристика Пуассона соответствует биномиальной оперативной характеристике. Последнее имеет место, если найденная пара значенийудовлетворяет условию (3.116) или, соответственно, условию (3.118).

Нужно еще отметить, что определенный с помощью (3.112) при заданных значениях иплан контроля по качественному признаку может в значительной степени зависеть от того, какое распределение случайной величиныберется за основу. Если за основу берут гипергеометрическое распределение, то получающийся объемвыборки будет меньше, чем в случае распределения Пуассона. Определенный при использовании распределения Пуассона план является также допустимым, хотя необязательно минимальным по объему планом для биномиального и гипергеометрического случая.

Имеется метод прямого, то есть одношагового вычисления и, базирующийся на преобразовании биномиального распределения с его последующей аппроксимацией нормальным распределением. Это приводит к следующей формуле для определения объема выборки:

, (3.121а)

где ;;- квантили нормированного нормального распределения.

При найденном вычисляют приемочное числосогласно выражению:

, (3.121б)

где .

При получении не целочисленных значений и, последние округляются до следующего целого числа.

Пример 3.51 Для партий объемом ищут план, который имеет приемлемый уровень качествас риском потребителяи браковочный уровеньс риском поставщика. Итак, нужно определить план, для которого, во-первых, согласно (3.112) выполняются неравенстваии, во-вторых, объем выборкиминимален. Будем исходить из того, что оперативная характеристика имеет распределение Пуассона.

Если случайная величина распределена по закону Пуассона, функцияимеет вид. Для вычисленияивоспользуемся таблицей квантилейраспределения. Итак,

;

…………………………………

.

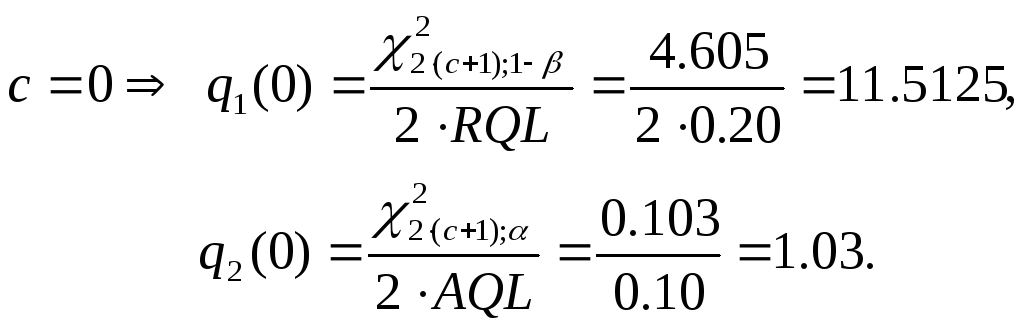
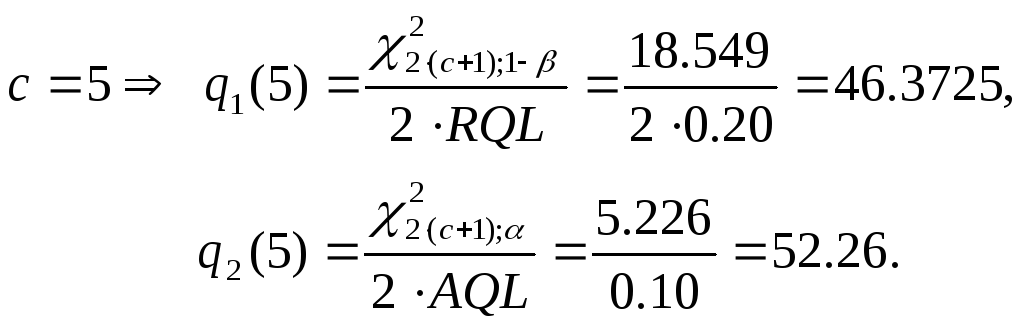
Итак, приемочным числом искомого плана контроля является . Каждое целочисленноев силу (3.120) может быть объемом допустимого плана, если выполняется условие. Здесь возможны значения. Выбираем наименьшее из этих значений.

Таблица 3.25 показывает, как выбор значения при том же числевлияет на действительные риски

,

.

Таблица 3.25 Влияние допустимых объемом выборок на действительные значения рисков в случае простого плана контроля

47	0.033	0.093
48	0.036	0.084
49	0.039	0.075
50	0.042	0.067
51	0.045	0.06
52	0.049	0.053

Пример 3.52 В предыдущем примере определялся план для случая распределения Пуассона, который обеспечивает приемлемый уровень качества си браковочный уровеньпри. Покажите, что найденный пландопустим и в биномиальном случае. Будет ли он в биномиальном случае также минимальным по объему.

Воспользуемся зависимостью (3.18) при и, получим:

Требуемые неравенства действительно выполняются, и поэтому план приемлем и в биномиальном приближении. Однако он уже не является минимальным по объему выборки, так как для этого случая и-.

Пример 3.53 Пусть приипри. Какие значения дляисогласно (3.120) получим при использовании распределения Пуассона? В каких пределах может изменятьсябез нарушения требований (3.120). Вычислите для каждого допустимогодействительный риск производителяи действительный риск поставщика.

……………………………………

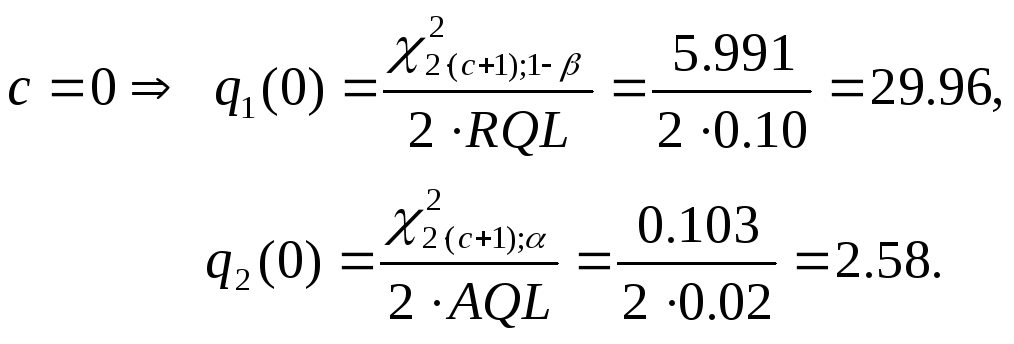
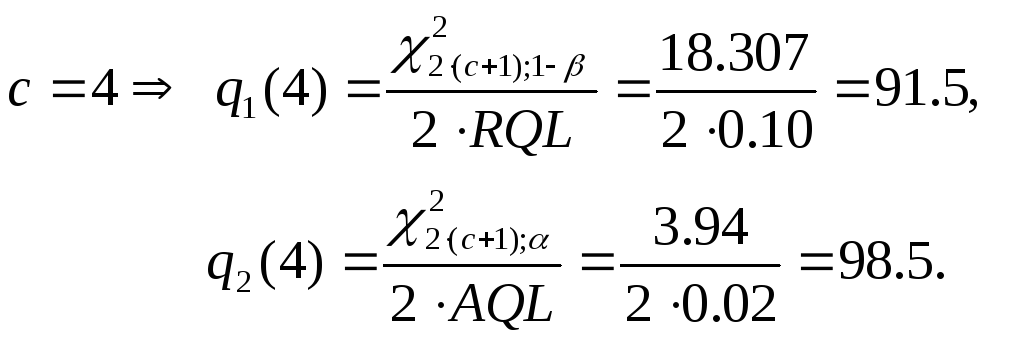
Итак, имеем .

Объем выборки может принимать следующие значения:. Для действительного рискаиприи названных значенияхпо формуламиполучаются значения, приведенные в табл.3.26.

Таблица 3.26 Влияние допустимых объемом выборок на действительные значения рисков в случае простого плана контроля

92	0.039	0.049
93	0.041	0.046
94	0.042	0.043
95	0.044	0.040
96	0.046	0.038
97	0.047	0.035
98	0.049	0.033

Пример 3.54 Найдите ипри данных из примера 3.51 по формуле (3.121).

;

;

; .

Используя эти значения, получаем:

,

то есть . С учетом этого,

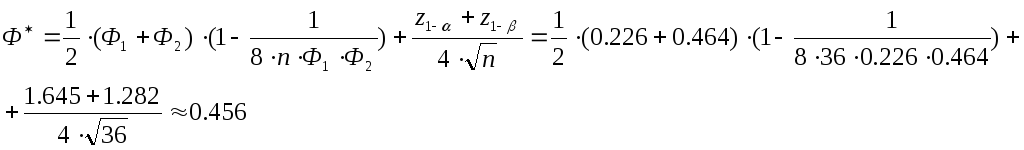Поэтому , то есть.

Таким образом, получаем и. Поверим условие (3.116), имеем

.

Таким образом, условие по предельно допустимому уровню дефектности не выполняется, поэтому план не приемлем.