2.2.1.2.1.6 Последовательный анализ

Для проверки статистических гипотез наряду со статистиче­скими критериями, основанными на анализе выборок заданного объема, находят также применение статистические критерии, в которых требуемый объем выборки , число взятия выбо­рок, необходимых для принятия решения, заранее не заданы. При использовании таких критериев в процессе проверки гипотез объем выборки последовательно увеличивают на единицу и каждый раз решают, достаточны ли имеющиеся данные для принятия реше­ния или нужно увеличивать выборку.

Такой вид статистических критериев относится к последова­тельному анализу и используется при разработке последователь­ных планов выборочного контроля и построении контрольных карт кумулятивных сумм.

Применяя этот вид статистических критериев, можно обойтись меньшими объемами выборок. Рассмотрим теорию последовательного анализа на примере, когда наблюдаемым показателем качества является, например, доля несоответствующих изделий и необходимо проверить только простую гипотезу против конкурирующей гипотезы.

Пусть задана случайная переменная , распределение которой в генеральной совокупности зависит от параметра. Переменнаяможет быть дискретной или непрерывной. Упрощенно примем, чтоможет иметь только значенияи. Проверить нужно гипотезы:

.

. (2.110)

Если из генеральной совокупности взять случайную выборку ) с возвращением, тоотношение вероятностей обнаружения в выборке несоответствующих изделий

(2.111)

является мерой правдоподобия для гипотез и. Значениебольшее единицы, говорит в пользу, значениеменьшее единицы - в пользу. Критерий, базирующийся на применении контрольной величины, называетсякритерием отношения вероятностей, сокращенно критерием (сокращение для словосочетания Likelyhood-Quotient) .

Классический критерий Ноймана-Пирсона построен по схеме, когда перед началом проведения процедуры проверки задается объем выборки и граничное значениеи по ним определяютсяи.

Разработанный А.Wald (1947) последовательный критерий отношения вероятностей работает с двумя граничными значениями и() и переменным объемом выборки. Основная идея этого критерия - контроль нужно продолжать до тех пор, пока не выполнится условие, то есть до тех пор, пока значениене будет близко к единице (для этого берут следующую выборку и для нее вычисляюти так до тех пор, пока не будет принята одна из гипотез). При наступлении событияпринимают решение в пользу, при- в пользу. На практике обычно определяют верхние границыидля вероятностей ошибок и с их помощью вычисляют граничные значенияи. Обычно принимается:

, (2.112а)

. (2.112б)

Применим последовательный критерий отношения вероятностей к случаю, когда наблюдаемый признак качества в конечной генеральной совокупности может принимать только два значения, соответствующие годному и дефектному изделию.

Генеральная совокупность (партия) распределена по закону Бернулли и параметр распределения , то есть доля брака в партии, неизвестен. Сначала примем для упрощения, чтоможет принимать только значенияи. Проверяем гипотезы

, (2.113)

.

при и заданных вероятностях ошибоки. Если из партии взять случайную выборку с возвращением объемом(при достаточно большом объеме партии это практически не имеет значения), тоявляется вероятностью получения реализациивыборочного вектораи поэтому функция правдоподобия для выборки имеет вид

.

При этом обозначает число обнаруженных в выборке дефектных изделий. Тогда отношение вероятностей (135) составляет

. (2.114)

Граничные значения иможно вычислить согласно (2.112) и в случаепринять гипотезу, а при- гипотезу. В случае, если, решение не принимается, берется еще одно изделие и вычис­ляетсяи т.д. Для практического использования критерия отношения вероятностей целесообразнее исходить не из условия, а из эквивалентного условия:

. (2.115)

Введем обозначения:

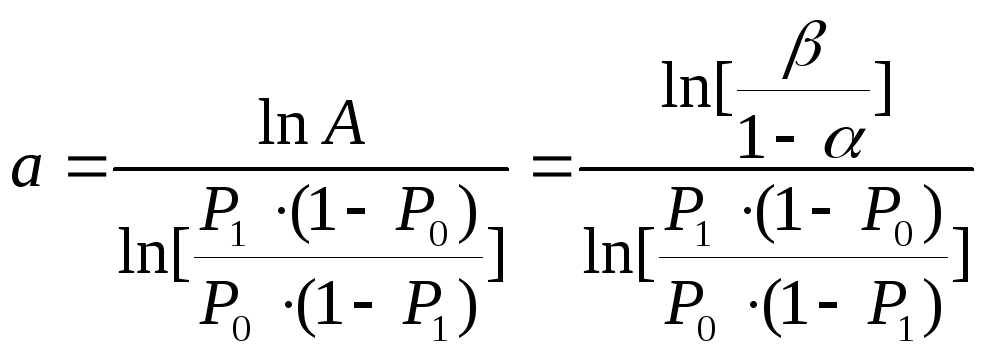, (2.116а)

, (2.116б)

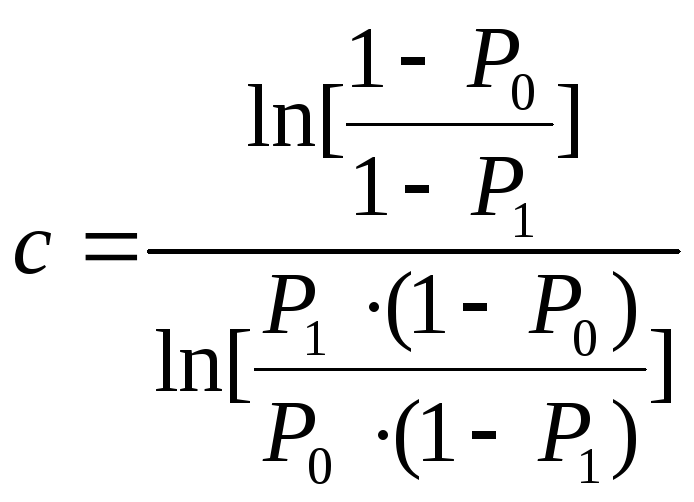, (2.116в)

и определим по (2.116) интервал

, (2.117)

где - накопленное число дефектных изделий.

Тогда получим цепочку эквивалентных отношений

.

При использовании последовательного критерия отношения вероятностей возможен и другой подход. Для начального объема выборки при заданныхвычисляют коэффициенты (2.116), а затем - границы интервала. Если число дефектных изделий отвечает условию, то принимается гипотеза; припринимается конкурирующая гипотеза. Если, то выборку увеличивают на одно изделие и процедура повторяется с новым значением.

Если границы интервала представить графически в виде функции от, то получим две последовательности точек, лежащих на параллельных полупрямых с наклоном. Верхняя полупрямая называетсябраковочной границей, нижняя - приемочной границей, а лежащее между ними пространство - областью продолжения испытаний (рис. 2.17).

Вышеизложенное без особых изменений можно применить и для сравнения гипотез:

(2.118)

при . Вероятности ошибок 1-го или 2-го рода здесь не определяются однозначно, как при проверке гипотез (2.113). Здесь можно только задать наибольшую вероятность ошибки 1-го рода на интервалеи наибольшую вероятность ошибки 2-го рода на интервале.

Пример 2.38 Пусть задано ии. Вычислите с этими значениями отношение вероятностей и объясните результат.

Решение. При заданных значениях

.

Этот результат свидетельствует о том, что выборочные данные при верности гипотезы в 41.58 раз более вероятны, чем при верности нулевой гипотезы.

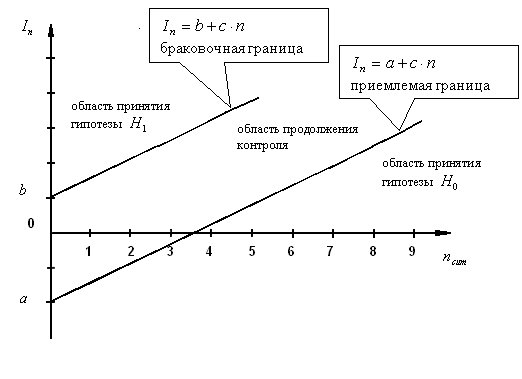
Рис.2.17 Диаграмма хода последовательного контроля

Применим последовательный критерий отношения вероятностей к генеральной совокупности, элементы которой (носители признака качества) обладают нормально распределенным признаком качества . Математическое ожиданиенеизвестно, дисперсия- известна. Предположим, что интересующий нас параметр может иметь только два возможных проявления: требуемый уровень настройкии нежелательный уровень. В этом случае проверяют гипотезы

(2.119)

с параметром и с заданными вероятностями ошибоки. Функция правдоподобия имеет вид:

.

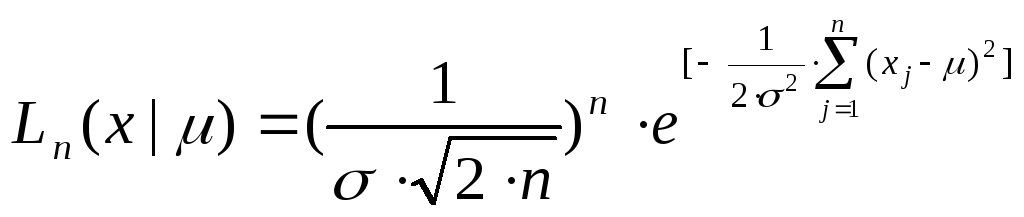Для отношения вероятностей получаем:

. (2.120)

Для начального значения вычислим контрольную величину и проверим, выполняется ли условиеили, гдеиопределяются по (2.112). В первом случае принимают гипотезу, во втором случае - гипотезу, а в последнем случаеувеличивается дои процедура повторяется.

Путем логарифмирования можно упростить процедуру проверки. Для контрольной величины получаем:

. (2.121)

При этом обозначает нормализованную путем деления насуммуотклонений выборочных значенийот математического ожидания

. (2.122)

Введем обозначения:

, (2.123а)

, (2.123б)

(2.123в)

и определим аналогично (2.117) интервал

. (2.124)

Тогда можно записать цепочку отношений эквивалентности

.

При использовании последовательного критерия отношения вероятностей можно действовать и другим способом: для начального значения при заданныхивычисляют параметрыи_, и тем самым - границы интервала . Если контрольная величинаимеет такое значение, чтоили, то принимают соответственно гипотезуили; в противном случае - продолжают проверку. Если верхние и нижние границы интервалананести на график в зависимости от, то получим две полупрямые, которые называются соответственнобраковочной и приемочной границами, а область между ними - областью продолжения контроля.

При проверке гипотез (2.119) предполагалась возможность положительного отклонения от математического ожидания . Соответственно можно проверить и гипотезы

(2.125)

при (проверка на отрицательное отклонение). Контрольный интервал определяется здесь как

,

где ивычисляются по (2.123). Комбинируя (2.119) и (2.125), приходим к возможности проверки гипотез

. (2.126)

Если вероятность ошибки 1-го рода распределить поровну между двумя возможными при гипотезе отклонениями, тообласть продолжения контроля определится интервалом

. (2.127)

В силу того, что делится на два возможных прислучая, тов (2.112) нужно заменить на, то есть необходимые для определенияпараметрыивычислять не по (2.123а, б), а как:

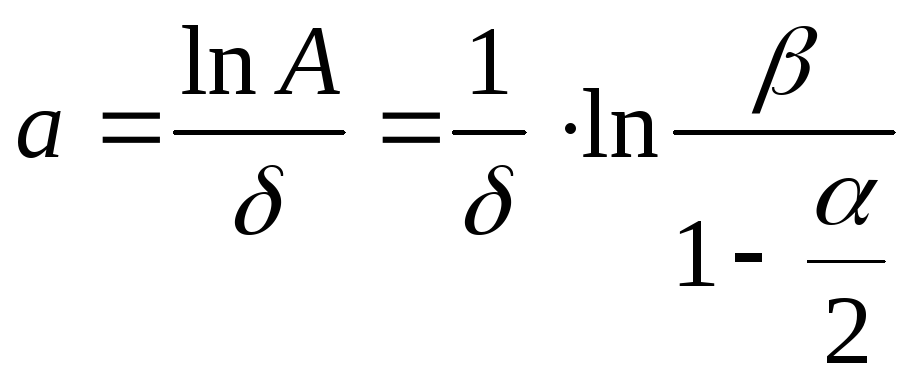, (2.128а)

. (2.128б)

Графически области продолжения контроля имеют форму двух полос, составляющих букву , лежащую вдоль горизонтальной оси. Внутренние и внешние границы этих полос и образуют здесь браковочные и приемочные границы.