2.2.1.2 Примеры проверки статистических гипотез

2.2.1.2.1Доверительные интервалы для оценки математического ожидания нормального распределения

2.2.1.2.1.1Среднее квадратическое отклонениеизвестно

Пусть количественный признак генеральной совокупности распределен нормально, причем среднее квадратическое отклонениеэтого распределения известно. Требуется оценить неизвестное математическое ожидание по выборочной средней. Необходимо определить доверительные интервалы, покрывающие параметрс надежностью, где- некоторое малое число.

Будем рассматривать выборочную среднюю как слу­чайную величину (изменяется от выборки к выборке) и выборочные значения признака- как одинаково распределенные независимые случайные вели­чины(эти числа также изменяются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равнои среднее квадратическое отклонение.

Как уже отмечалось выше, если случайная вели­чина распределена нормально, то выборочная средняя, найденная по независимым наблюдениям, также рас­пределена нормально.

Потребуем, чтобы выполнялось соотношение , где- заданная доверительная вероятность (надежность).

Воспользуемся формулой (2.66):

,

где . (2.73)

Кроме того, обозначим параметры распределения :

; (2.74а)

. (2.74б)

Выразим точность оценки через зависимость (2.74б) получим:

. (2.75)

Таким образом, при заданной вероятности окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим):

. (2.76)

Смысл полученного соотношения таков: с надежностью можно утверждать, что доверительный интервалпокрывает неизвестный параметр. Точность оценки.

Итак, поставленная задача решена. Число определяется из равенства, или. По табл.2.2 находят аргумент, которому соответствует значение функции, равное.

Примечание 1. Оценку называют классической. Из формулы , определяющей точность классической оценки, можно сделать следующие выводы:

- при возрастании объема выборки числоубывает и, следовательно, точность оценки увеличивается;

- увеличение надежности оценки (доверительной вероятности) приводит к увеличению[возрастающая функция] и, следовательно, к возрастанию . Другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.

Примечание 2. В национальном стандарте ГОСТ Р 50779.21 «Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение» приведен следующий алгоритм точечного и интервального оценивания среднего значения при известной дисперсии.

Исходные данные: объем выборки - ; сумма значений наблюдаемых величин -; известное значение дисперсии -; выбранная доверительная вероятность -.

Алгоритм вычислений: по таблицам определяют квантили нормированного нормального закона распределения - и; вычисляют

Тогда точечная оценка математического ожидания - .

Двухсторонний симметричный доверительный интервал для математического ожидания :

или .

Односторонние доверительные интервалы для математического ожидания :

или

.

Следствием настоящих зависимостей является алгоритм решения задачи сравнения неизвестного среднего значения с заданным значением математического ожидания(центром поля допуска контролируемого параметра) при известной дисперсии:

- в двухстороннем случае предположение равенства выборочного среднего значения и заданного математического ожидания(нулевая гипотеза)отклоняется, если:

;

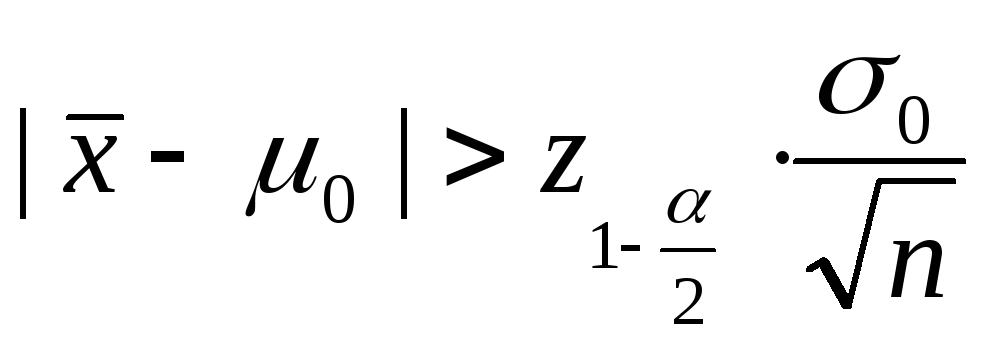- в одностороннем случае предположение о том, что выборочное среднее не меньше чем(нулевая гипотеза)отклоняется, если:

;

- в одностороннем случае предположение о том, что выборочное среднее не больше чем(нулевая гипотеза) отклоняется, если:

.

В качестве примера использования – проверка правильности настройки технологического процесса на середину поля допуска или на заданное значение, при этом точность технологического процесса предполагается известной или заранее оцененной. Невы­полнение этих условий свидетельствует о несоответствии фак­тического центра группирования контролируемого параметра в изготавливаемой партии изделий центру поля допуска, что мо­жет привести к повышению уровня брака на последующих тех­нологических операциях.

Настоящий подход применяется и при решении задачи о сравнении двух неизвестных средних значений ипри известных дисперсияхи. В этом случае высчитывают:

- ;

-

- .

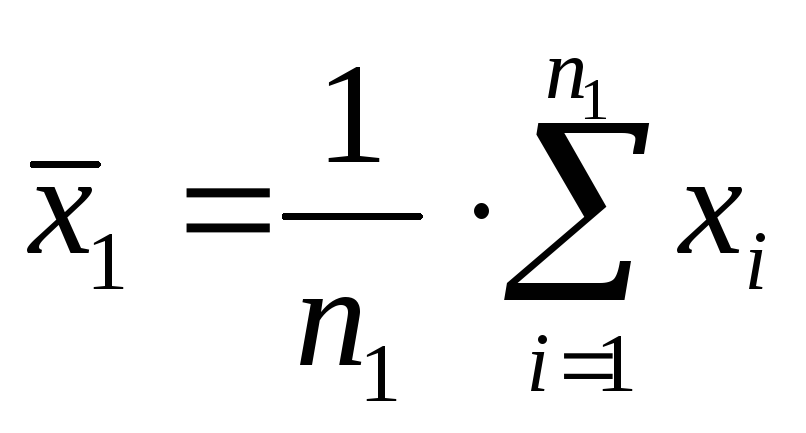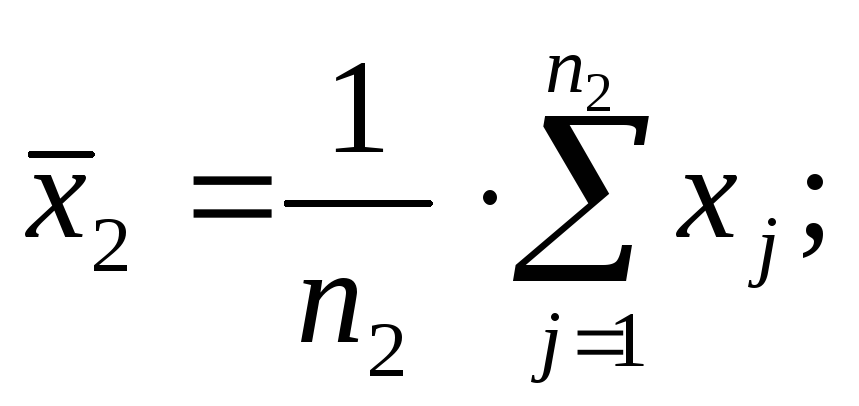
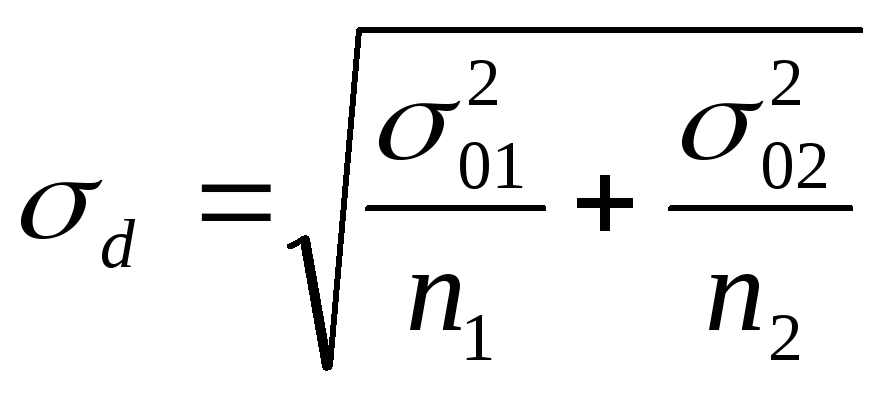Тогда сравнение средних значений двух совокупностей:

- в двухстороннем случае предположение равенства средних значений (нулевая гипотеза) отклоняется, если:

;

- в одностороннем случае предположение о том, что первое среднее не меньше второго(нулевая гипотеза) отклоняется, если:

;

- в одностороннем случае предположение о том, что первое среднее не больше второго(нулевая гипотеза) отклоняется, если:

.

В качестве примера использования – технологический процесс проводят на двух станках, точность каждого из них известна и. Можно ли считать, что оба процесса одинаковы, и смешивать детали, произведенные на этих двух станках.

Пример 2.31. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением. Найти доверительные интервалы для оценки неизвестного математического ожиданияпо выборочным средним, если объем выборкии задана доверительная вероятность.

Найдем . Из соотношения, получим. По табл.2.2 находим. Найдем точность оценки:.

Доверительный интервал таков: . Например, если, то доверительный интервал имеет следующие доверительные границы -.

Таким образом, значения неизвестного параметра , согласующиеся с данными выборки, удовлетворяют неравенству. Подчеркнем, что было бы ошибочным написать. Действительно, так как- постоянная величина, то либо она заключена в найденном интервале (тогда событиедостоверно и его вероятность равна единице), либо в нем не заключена (в этом случае событиеневозможно и его вероятность равна нулю). Другими словами, доверительную вероятность не следует связывать с оцениваемым параметром. Она связана лишь с границами доверительного интервала, которые, как уже было указано, изменяются от выборки к выборке.

Поясним смысл, который имеет заданная надежность. Надежность (доверительная вероятность) указывает, что если произведено достаточно большое число выборок, то 95 % из них определяет такие доверительные интер­валы, в которых параметр действительно заключен. Только в 5 % слу­чаев он может выйти за границы доверительного интервала.

Примечание 3. Если требуется оценить математическое ожида­ние с наперед заданной точностьюи надежностью, то минималь­ный объем выборки, который обеспечит эту точность, находят по формуле

(2.77)

(следствие равенства ).
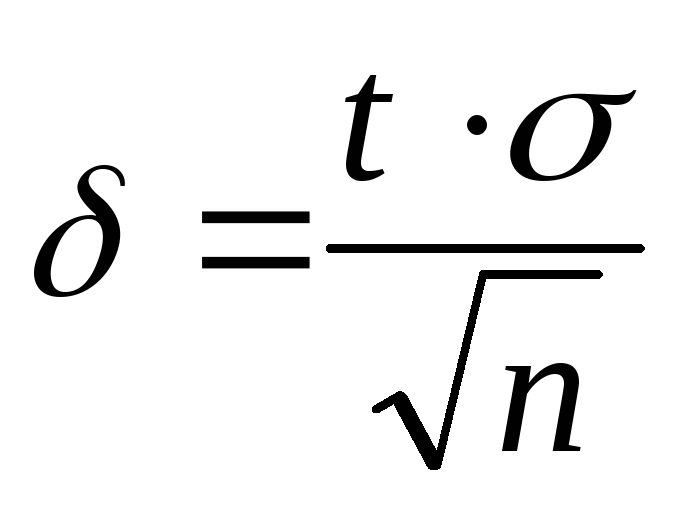