
telnov-machanika-and-TO
.pdf
X
x(t)
|
|
|
|
|
|
|
t0 |
|
t |
|
|
||
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
|||
Производная функции x(t) в точке t0 |
|
|
|
(7.1) |
|||||||||
|
|
dx(t0) = x(t0 +dt) -x(t0) . |
|
||||||||||
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
Рассмотрим |
простейший пример: x(t) = at2 , |
где a = const . |
|||||||||||
Подставляя в (7.1) получаем |
|
|
|
dt 0 |
|
||||||||
|
|
|
|
|
|
2at dt +a(dt) |
|
|
|
||||
dx(t) = a(t +dt) |
-at |
= |
|
|
|
|
2 |
= 2at +adt |
= 2at . |
(7.2) |
|||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
|
|
|
|
|
dt |
|
|
|
|
Используются различные обозначения производной:
dx(t) - по Лейбницу dt
x¢(t)- по Лагранжу
x - по Ньютону
Все это мгновенная скорость v(t). Ускорение, по определению
a(t) = |
v(t +dt) -v(t) |
|
dv |
¢ |
(7.3) |
||
|
dt |
|
= dt |
º v (t) º v(t) |
|||
Выразивv(t) через x(t) , получаем |
|
|
|
||||
|
a(t) = |
d2x(t) |
º x |
¢¢ |
|
(7.4) |
|
|
dt2 |
(t) = x(t). |
|||||
Выпишем производные от элементарных функций, часто встречающихся в физических задачах (подробности в курсе мат. анализа)
21

f (x)
const
xn
1
xn x
x
1 x
f ¢(x)
0
nxn-1
-xnn+1
1
1
2x
-x12
f(x) |
¢ |
|
f (x) |
|
|
ex |
ex |
|
ln x |
1 / x |
|
sin x |
cos x |
(7.5) |
cos x |
- sin x |
|
tg x |
1 / cos2 x |
|
ctg x |
-1 / sin2 x |
|
Дифференцирование произведения и дроби функций: Пусть f (x) = u(x)v(x) , тогда
df |
= |
|
u(x +dx)v(x +dx) -u(x)v(x) |
= |
|
|
|
dx |
|
|
|
||||
|
|
|
dx |
|
|
|
|
|
¢ |
¢ |
|
|
|
||
|
= |
(u(x) +u (x)dx)(v(x) +v (x)dx) -u(x)v(x) |
= |
(7.6) |
|||
|
|
||||||
|
|
|
|
dx |
|
|
|
|
dx 0 |
|
|
|
|
||
|
¢ |
¢ |
|
|
|
||
|
= u (x)v(x) +u(x)v (x) |
|
|
|
|||
Аналогично находятся производные от любых произведений и дробей, в частности
f (x) |
|
|
¢ |
|
|
|
|
|
|
f (x) |
|
|
|
||
u(x)v(x) |
¢ |
¢ |
|
|
|
||
u (x)v(x) +u(x)v (x) |
|
|
|||||
u(x)v(x)g(x) |
¢ |
|
¢ |
¢ |
(7.7) |
||
u (x)v(x)g(x) +u(x)v |
(x)g(x) +u(x)v(x)g (x) |
|
|||||
u(x) |
¢ |
¢ |
|
|
|||
|
u (x)v(x) -u(x)v |
(x) |
|
|
|||
v(x) |
|
|
|
v2(x) |
|
|
|
22
Дифференцирование сложной функции: Пусть естьf (u), где u = g(x). Тогда
|
|
|
df = df du . |
|
(7.8) |
|
|
|
|
dx |
du dx |
|
|
Например: |
f (x) = sin2 x . Здесь |
f = u2 , где |
u = sin x . Находим |
|||
df |
= 2u, |
du |
= cos x , следовательно df |
= 2 sin x cos x = sin 2x . |
||
du |
|
dx |
|
dx |
|
|
Используя эти довольно простые правила, можно найти производную от любой функции, являющейся комбинацией элементарных математических функций. Задача всегда имеет решение.
При движении в пространстве удобно использовать векторное описание, при этом мгновенная скорость, рис. 12,
r |
v(t) = lim r(t + Dt) - r(t) |
= dr |
(7.9) |
||||||||
|
Dt 0 |
|
Dt |
|
|
|
|
|
dt |
|
|
r(t dt) |
Аналогично |
a(t) = dv |
= d2r . |
(7.10) |
|||||||
r(t) |
|
|
|
dt |
|
|
dt2 |
|
|||
|
В декартовых кординатах |
|
|
|
|
||||||
|
|
|
|
æ |
|
dy |
|
dz |
ö |
|
|
|
v = (v |
,v |
,v |
çdx |
, |
, |
÷ |
(7.11) |
|||
Рис. 12 |
) = ç |
|
|
|
÷. |
||||||
x |
y |
z |
ç |
|
dt |
|
dt |
÷ |
|
||
|
|
|
|
èdt |
|
|
ø |
|
|||
vz |
Годограф |
Конец вектора r(t) |
описывает |
|||
траекторию в X,Y,Z -пространстве. |
||||||
|
скорости |
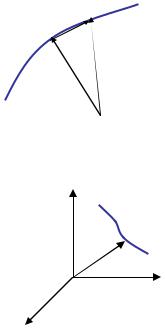
По аналогии можно нарисовать то же |
||||
|
v(t) |
для скорости, рис. 13. Такую кривую в |
||||
|
|
|||||
|
vy |
пространстве скоростей |
называют |
|||
vx |
годограф |
скорости. |
Он |
показывает |
||
|
||||||
|
какие значения принимает скорость во |
|||||
|
|
время |
движения. |
Это |
понятие |
|
|
Рис. 13 |
используется редко. |
|
|
||
|
|
|
|
|
||
23

§ 8. Обратная задача кинематики
При движении под действием силы известно ускорение a(t) и необходимо найти v(t) и r(t).
В одномерном случае перемещение – это плошадь под кривой v(t),
рис, 14, которая находится как сумма малых перемещений. При стремлении шага суммирования к нулю сумма переходит в
определенный интеграл
t |
|
x -x0 = åviDti = ò v(t)dt . |
(8.1) |
i |
t0 |
|
Примечание: следует различать «перемещение» и «пройденный телом путь». Перемещение в (одномерном случае) – это разница координат конечной и начальных точек
|
|
|
|
t2 |
|
||||
|
|
|
|
|
|||||
|
|
|
|
S = ò v(t)dt. |
(8.2) |
||||
|
|
|
t |
t1 |
|
||||
|
|
|
Путь пройденный телом – это |
|
|||||
t0 |
|
t |
t2 |
|
|||||
|
S = ò |
|
v(t) |
|
dt. |
(8.3) |
|||
|
|
||||||||
|
|
|
Рис. 14 |
t1 |
|
||||
|
|
|
|
Например, автомобиль |
целый |
||||
день ездил по городу и вернулся в гараж, тогда перемещение равно нулю, а путь равен изменению показаний одометра (счетчика пробега). Таким образом, путь и перемещение равны только при одномерном движения в одном направлении.
Итак, известна скорость v(t), нужно найти путь S(t), как это сделать математически? Поскольку мы знаем, что v(t) = S ¢(t) , то задача сводится к нахождению такой функции S(t), чтобы ее производная равнялась скорости v(t). Эта задача, обратная нахождению производ-
ной, называется взятием интеграла от функции. Интеграл от f(x)записывается так
ò f (x)dx =F(x) +const , |
(8.4) |
где функция F(x) такая, что F ¢(x) = f (x) , ее называют первообразной функцией от f(x). Константа в (8.4) отражает тот факт, что
24
первообразная определена с точностью до константы, поскольку
¢ |
¢ |
производная от константы равна нулю: ((F(x) +const) |
= F (x) . |
Поэтому такой интеграл называют неопределенным интегралом. Можно представить, что неопределенный интеграл – это площадь под кривой f(x), где x меняется от некого постоянного, но
неопределенного значения, до переменного значения x .
Для того, чтобы найти площадь S в области a < x <b нужно от значения неопределенного интеграла в точке b отнять его значение в точке a , при этом константа выпадет и получается определенный интеграл, равный разности значений первообразной в точках b и a
b |
|
S = ò f (x)dx = F(b) -F(a). |
(8.5) |
a
Таким образом обратная задача кинематики сводится к взятию интегралов, т.е. нахождению первообразных.
Для некоторый функций интеграл находится сразу, например, поскольку (sin x)¢ = cos x , то ò cos x dx = sin x +const . В отличие от
процедуры нахождения производной, взятие интеграла является более сложной задачей. Не для всякой функции, состоящей из элементарных функций, можно найти первообразную, выражающуюся через элементарные функции.
Если функция сложная и интеграл не берется, то для физиков это не проблема, т.к. любой определенный интеграл можно быстро найти с помощью компьютера, разбив отрезок ab на малые отрезки Dx и
просуммировав f (xi )Dx . Однако, всегда приятно когда ответ задачи
можно выразить не числом, а формулой для произвольных a и b . Техника нахождения интегралов излагается в курсе
математического анализа. Ниже приведена таблица некоторых простейших интегралов
ò xndx = |
xn+1 |
|
, (n - действ. число, n ¹ -1) |
ò |
|
n +1 |
|||||
|
|
|
|||
ò dx = ln | x |, |
(x ¹ 0) |
ò |
|||
x |
|
|
|||
ò exdx = ex |
|
ò |
|||
sin x dx = -cos x |
|
cos x dx = sin x |
(8.6) |
tg x dx = -ln | cos x |. |
|
Пример: пусть скорость v =bt2 (b –число), найти перемещение за время от t1 до t2 . Ответ находится путем взятия определенного
интеграла
25

t2 |
|
|
|
|
|
x = òbt2dt = b t3|t2 |
= b |
(t23 |
-t13 ). |
(8.7) |
|
3 |
t1 |
3 |
|
|
|
t1 |
|
|
|
|
|
Эту же задачу можно сформулировать несколько иначе: пусть скорость v =bt2 , найти как путь (перемещение) зависит от времени,
если x = x0 в момент t0 . В этом случае берется неопределенный интеграл, а константу находится из начальных условий:
x = òbt2dt = b t3 |
+const . |
(8.8) |
3 |
|
|
Подставляя сюда x = x0 , t = t0 находим const = x0 - b3 t03 . Окончательный ответ
x = x |
0 |
+ b (t3 -t3 ). |
(8.9) |
|
|
3 |
0 |
|
|
|
|
|
|
|
Мы расмотрели прямую и обратную задачю кинематики в декартовой системе кординат. Она сводиться к простому дифференцированию и интегрированию по каждой из проекций.
В векторной форме
t
r(t) = ò v(t) dt + r(t0 ),
t0 |
(8.10) |
t |
v(t) = ò a(t) dt + v(t0 ).
t0
Здесь каждое векторное уравнение является удобной записью трех уравнений для движения по каждой проекции.
Еще немного математики.
В физике часто требуется упростить формулы, содержащие малые величины, сохранив при этом главные члены содержащие эти малые величины. Приведем некоторые полезные математические приемы.
1. |
f (x) = 1 + x » 1 + x |
, где x 1. |
(8.11) |
|
2 |
|
|
Это нетрудно проверить, возведя обе части в квадрат, получается слева 1 + x , справа 1 + x + x2/4 . Последним членом можно
пренебречь, т.к. он следующего порядка малости по сравнению со вторым членом, содержащим x .
26

2.f (x) = 11 ++ ab , где a, b 1.
Домножая числитель и знаменатель на (1 -b) и пренебрегая членами второго порядка малости, получаем
f (x) = 1 + a = (1 + a)(1 - b) = 1 + a - b -ab » 1 + a - b . (8.12) 1 + b (1 + b)(1 -b)
Ряд Тейлора
Любую гладкую функцию вблизи точки точки a можно разложить в ряд Тейлора
¢ |
1 |
|
¢¢ |
2 |
|
1 |
|
n |
|
n |
. |
(8.13) |
2! f |
|
+ n ! f |
|
(a)x |
|
|||||||
f (a + x) = f(a) + f (a) x + |
(a)x |
|
|
|
||||||||
Действительно, продифференцировав выражение один раз (учитывая, что (xn )¢ = nxn-1 ), получаем f ¢(a + x) = f ¢(a) + члены, содержащие
малый параметр x . Продифференцировав дважды, получаем
f ¢¢(a +x) = f ¢¢(a)+ малые члены, и т.д., Тем самым мы проверили, что
при малых x производные всех порядков у функций слева и справа равны. Такое может быть только, если равны сами функции. Разложение в ряд некоторых функций, которые нам понадобятся в дальнейшем,
ex = 1 +x + x2 + x3 |
, |
(8.14) |
||
2 |
6 |
|
|
|
ln(1 + x) = x - x2 |
, |
(8.15) |
||
2 |
|
|
|
|
sin x = x - x3 |
, |
|
|
(8.16) |
6 |
|
|
|
|
cos x = 1 - x2 |
, |
|
|
(8.17) |
2 |
|
|
|
|
tg x = x + x3 . |
|
|
(8.18) |
|
3 |
|
|
|
|
Во всех приведенных примерах предполагается x 1.
27

§ 9. Ускорение при криволинейном движении
Движение по окружности
Y |
|
Сначала |
|
рассмотрим |
равномерное |
||||||||
|
движение по окружности в декартовых |
||||||||||||
|
|
кординатах, рис.15. Пусть точка |
|||||||||||
v |
|
движется по окружности радиуса R . |
|||||||||||
R |
|
Радиус |
|
вектор |
|
|
точки составляет |
угол |
|||||
|
X |
j = wt |
отностительно оси |
X , где |
w – |
||||||||
|
|
угловая скорость. За период обращения |
|||||||||||
|
|
T = 2pR v |
|
приращение угла поворота |
|||||||||
|
|
равно wT = 2p , отсюда |
|
|
|||||||||
Рис. 15 |
|
w = |
2p |
= |
|
v |
|
|
|
(9.1) |
|||
|
|
T |
R |
|
|
|
|||||||
Учитывая, что x = R cosj, y = R sinj , получаем |
|
|
|||||||||||
x = R cos wt |
|
x = -Rw sin wt |
|
|
|
|
|
x = -Rw2 cos wt |
(9.2) |
||||
y = R sin wt |
y = Rw cos wt |
|
|
|
|
|
y = -Rw2 |
sin wt |
|||||
|
|
|
|
|
|
||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = -w2x, |
y = -w2y |
|
|
|
(9.3) |
|||||||
|
|
2 |
|
|
|
v2 |
çæ r ÷ö |
|
|
||||
или |
|
r = -w |
r = - |
|
|
ç |
|
|
÷, |
|
(9.4) |
||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
R |
ç |
|
÷ |
|
|
||
|
|
|
|
|
|
èRø |
|
|
|||||
|
где |
r = i x + jy |
– |
радиус-вектор точки, |r|º R . |
|||||||||
vПолучается, что ускорение направлено к центру
vокружности.
d |
|
|
Рассмотрим тоже самое в полярной системе |
|
координат, рис. 16. При смещении точки на угол |
||
|
R |
||
|
dj |
вектор v поворачивается на этот же угол. |
|
|
|
||
Изменение вектора скорости находим совместив начала начального и конечного векторов скорости. Тогда вектора начальной, конечной скорости и изменения скорости образуют равнобедренный треугольник с углом при
вершине dj. Изменение скорости по модулю равно
dv = 2v sin(dj/2) » vdj, |
(9.5) |
а вектор изменения скорости направлен к центру окружности
28

dv = -er vdj |
(9.6) |
где er – вектор единичной длины, направленный вдоль радиусавектора точки. Отсюда ускорение
a |
|
= dv |
= -e |
v dj |
= -e |
v w = -e |
v2 . |
(9.7) |
|
n |
dt |
r |
dt |
r |
|
r R |
|
При равномерном |
движении |
по |
окружности точка |
имеет |
||||
центростремительное ускорение an , перпендикулярное скорости
(«нормальное» ускорение). Этот результат эквивалентен формуле (9.4). Если меняется абсолютное значение скорости, то кроме центростремительного ускорения добавляется тангенциальное
ускорение at , направленное вдоль окружности (вдоль направления скорости) равное
a |
|
= e |
dv |
, |
(9.8) |
|
t |
|
j dt |
|
|
где ej - единичный вектор в направлении скорости, v – модуль скорости (скаляр). Полное ускорение при движении по окружности
a = a |
|
+ a |
|
= -e |
v2 |
+ e |
dv . |
(9.9) |
|
n |
|
t |
|
r R |
|
j dt |
|
Тангенциальное и нормальное ускорение при произвольном движении
Рассмотрим случай произвольного движения. Известно , что через любые три точки можно провести окружность. Выберем три ближайшие точки на траектории и проведем окружность. Как было показано выше, полное ускорение будет суммой тангенцального и нормального ускорений
a = a |
n |
+ a |
t |
= n v2 |
+ tdv |
(9.10) |
|
|
R |
dt |
|
||
|
|
|
|
|
Здесь n = -er – единичный вектор в направлении центра окружности, t = ej – единичный вектор в направлении скорости. Отсюда получаем способ нахождения R. Поскольку t и n перпендикулярны, то
1 |
= |
an |
= |
a2 -at2 |
= |
v2 -v2 |
. |
(9.11) |
R |
v2 |
v2 |
|
|||||
|
|
|
v2 |
|
||||
29

Для равномерного движения |
v |
= v dj = vw, |
v |
= 0, |
|
тогда |
1 |
= w . |
|||||||||||||||
R |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
v |
||
Другой способ нахождения радиуса кривизны: |
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
= |
an |
; |
a |
|
=| a |
|
|=| a - a |
|
|= |
a - |
|
(av) |
v |
. |
|
(9.12) |
||||
|
R |
|
n |
n |
t |
|
|
||||||||||||||||
|
|
v2 |
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
||||||||
Здесь (av) – |
скалярное |
произведение, |
модуль |
|
вектора—это |
||||||||||||||||||
A = Ax2 + Ay2 . Если, известны декартовы компоненты скорости и
ускорения, то по этой формуле легко найти радиус кривизны. Рассмотрим еще один способ нахождения R, используя векторное
произведение. Поскольку нормальная составляющая ускорения равна полному ускорению умноженному на синус угла между ускорением и скоростью, то она может быть записана в виде
a |
n |
=| a |
n |
|= | a × v | . |
(9.13) |
|
|
| v | |
|
||
|
|
|
|
|
Если ускорение и скорость лежат в плоскости X-Y, то единственная составляющая векторного произведения неравная нулю направлена по Z. Используя формулу (6.6) для векторного произведения, находим
|
|
| a × v |=| xy -yx |, |
(9.14) |
||||||
1 |
= |
an |
= |
| a × v | |
= |
|
| xy -yx | |
. |
(9.15) |
R |
v2 |
|v |3 |
|
||||||
|
|
|
(x2 +y2 )3/2 |
|
|||||
§ 10. Прямая задача кинематики в полярной системе кординат
В некоторых случаях, например при описании движении планет, удобно ползоваться не декартовой, а полярной системой координат.
e er |
Введем |
вектор |
er вдоль |
радиус-вектора, |
ej |
|||
поперек |
радиус-вектора |
в |
направлении |
|||||
r |
увеличения угла. |
Радиус-вектор |
произвольно |
|||||
движущейся точки |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
j |
|
r = err . |
|
(10.1) |
|
|||
Рис. 17 |
При движении |
|
меняется |
и |
длина |
r |
и |
|
направление er . Нетрудно видеть, что |
|
|
||||||
|
|
|
||||||
der = eφdj, |
dej = -erdj или |
er |
= eφj, |
ej = -erj. |
(10.2) |
|||
30
