
telnov-machanika-and-TO
.pdf
Решение. В лабораторной |
системе Fx =e cos q , |
Fy =e sin q |
|||||
Учитывая, чтоV º v º vx из (43.4), (43.5) получаем |
|
||||||
|
F -V |
(Fv) |
|
||||
Fx¢ = |
x |
c2 |
|
|
= e cos q , |
(43.17) |
|
1 - |
Vvx |
|
|||||
|
|
|
|
||||
|
c2 |
|
|||||
|
|
|
|
||||
Fy¢ = |
Fy 1 -V 2 c2 |
= |
e sin J |
, |
(43.18) |
|||
|
Vvx |
|
||||||
|
1 - |
|
1 -v2 c2 |
|
||||
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. продольная сила та же, а поперечная в g раз больше. |
|
|||||||
§44. Релятивистская ракета
Впредыдущих параграфах были рассмотрены физические основы Специальной теории относительности (СТО), имеющей дело с инерциальными системами отсчета. Далее мы рассмотрим несколько примеров использования СТО. Сначала совершим увлекательный полет на релятивистской ракете через всю Вселенную; затем рассмотрим столкновения и распады частиц – основной метод изучения материи; далее покажем, что вся электродинамика является следствием закона Кулона, СТО и инвариантности заряда.
Для разминки рассмотрим простую задачу. У нас есть ракета, которая может летать со скоростью V, и нужно слетать до звезды, находящейся на расстоянии L. Какое потребуется время?
Здесь можно рассуждать двумя способами:
а) время полета в лабораторной системе t = L/V , часы на ракете
идут в g = 1 / 1 -V 2/c2 раз медленнее, значит, по часам на ракете пройдет время t = t/g = L/gV ;
б) в системе ракеты расстояние Земля-звезда сокращается в g раз,
звезда летит навстречу со скоростью V , значит, по часам в ракете пройдет время t = L/gV , т.е. столько же.
А теперь перейдем к основной задаче: Релятивистская ракета,
равноускоренная в собственной системе отсчета. Кинематика
В качестве интересного упражнения по теории относительности рассмотрим движение космического корабля, имеющего постоянное
111

ускорение в собственной системе отсчёта, направленное вдоль скорости. Космонавты предпочитают лететь с комфортом, и их корабль имеет ускорение g.
В сопутствующей системе отсчёта S ¢ уравнение движения имеет
вид |
|
Fx¢ = max¢ = mg . |
(44.1) |
Найдем уравнение движения в системе Земли (S ), относительно которой корабль имеет мгновенную скорость v =V . Из формулы
преобразования сил (43.6) видим, что поскольку vx ¢ корабля равна
нулю, |
|
то |
Fx = Fx¢ |
|
|
Отсюда |
|
|
получаем уравнение |
|
движения в |
||||||||||||||||||||||||||||||||||||
неподвижной системе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
dp º |
d |
(gmv) = F = mg . |
|
|
|
|
|
|
|
|
|
|
|
(44.2) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
dt |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при t |
= |
|
0, |
находим |
||||||||||||||||
Интегрируя уравнение с учётом того, что v = 0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
mgv = mgt или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
v |
|
= gt |
v = |
|
|
|
|
|
|
|
|
gt |
|
|
g = 1 + g2t2 |
c2 |
. |
(44.3) |
||||||||||||||||||||||||||
|
1 -v2 c2 |
|
|
|
1 + g2t2 c2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Используя разложение |
|
|
1 + a » 1 + a 2 |
|
|
при a 1, получаем |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
2 2 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
g t |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
gt c 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
v |
» gt ç1 - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
÷, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
2c |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(44.4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
c |
2 |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
gt c 1. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
v |
» c ç1 |
- 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
÷, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
2g t |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Путь, пройденный кораблем в неподвижной системе |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
t |
|
|
gtdt |
|
|
|
|
|
|
|
c |
2 (gt c)2 |
|
|
dy |
|
|
|
|
c |
2 |
æ |
|
|
|
|
2 2 |
|
|
|
|
ö |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
g t |
|
|
|
|
÷ |
|
|
|||||||
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
÷ |
. |
(44.5) |
||
|
x = |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
1 |
+ |
|
2 |
|
|
|
|
÷ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
g |
ç |
c |
|
|
-1÷ |
|||||||||||||||||||||
|
|
|
|
|
|
|
2 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
2 1 +y |
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
÷ |
|
|
||||||||||
|
|
|
0 |
1 + g t |
c |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При gt |
c 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = gt2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(44.6) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при gt |
c 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
c |
2 |
æ |
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
ö |
|
|
c |
3 |
|
|
|
c |
2 |
|
|
|
|
c |
2 |
|
|
|
|||||||
|
|
|
|
|
|
çgt |
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
» |
g |
ç |
|
g2t2 |
+1 |
|
-1÷ » ct + |
|
|
2g2t |
- |
|
g |
~ ct - |
|
g |
. |
|
(44.7) |
||||||||||||||||||||||||
|
|
|
|
|
ç c |
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
112
Предположим, что через время T после старта ракеты вслед ей с Земли посылают световой сигнал. Пройденный им путь
x = c(t -T) = ct -cT. |
(44.8) |
Сравнивая с (44.7), видим, что при T >c g свет никогда не догонит
g свет никогда не догонит
ускоряющийся космический корабль! При земном ускорении свободного падения g = 103 см/сек T = c/g = 3 107 сек » 1 год.
Космонавты всё время будут "видеть" в свой телескоп изображение Земли, но движение на ней будет замедляться, и в пределе будет застывшая картинка Земли, "состарившейся" всего на 1 год. Кроме того, за счет эффекта Доплера изображение будет «краснеть», а также тускнеть.
Найдем теперь время t , прошедшее по часам на корабле. В соот-
ветствии с (16.3) или (25.12)
dt = dt 1 -v2 c2 = 1 g . |
(44.9) |
Подставляя сюда g из (44.3), получаем
|
|
t |
|
|
|
|
|
|
|
|
|
|
æ |
ö |
|
|
|
ò |
|
|
dt |
|
|
|
|
|
c |
|
çgt ÷ |
|
|
t = |
|
|
|
|
|
|
= |
|
|
arcshç |
÷ |
º |
|||
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
2 2 |
c |
2 |
|
|
g |
|
ç |
÷ |
|
|||
|
|
0 |
+ g t |
|
|
|
|
è c ø |
|
||||||
|
c |
|
æ |
|
|
|
2 |
2 |
|
2 |
ö |
|
|
||
º |
|
çgt |
|
|
|
c |
÷ |
|
|
||||||
|
lnç |
+ 1 + g t |
|
|
÷. |
|
|
||||||||
|
g |
|
ç |
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
è c |
|
|
|
|
|
|
|
|
ø |
|
|
||
И наоборот |
|
|
|
|
|
|
|
æ |
|
ö |
|
|
|
||
|
|
|
|
|
gt |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
çgt÷ |
|
|
|
||||
|
|
|
|
|
|
= shç |
|
÷. |
|
|
|||||
|
|
|
|
|
c |
|
|
ç |
|
÷ |
|
|
|
||
|
|
|
|
|
|
|
è |
c ø |
|
|
|
||||
(44.10)
(44.11)
Выше мы использовали гиперболические косинус и синус, имеющие следующие свойства
chx |
= |
ex +e-x |
, shx = |
ex |
-e-x |
2 |
2 |
x = 1, |
|
2 |
|
2 |
, ch |
x -sh |
(44.12) |
||||
|
¢ |
¢ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
(chx) = shx, |
(shx) = chx. |
|
|
|
|
||||
При gt c <<1, |
|
t » t , |
|
|
|
|
(44.13) |
||
gt c >> 1 |
|
|
t » c |
ln |
2gt . |
|
|
|
(44.14) |
|
|
|
g |
|
c |
|
|
|
|
113

Подставляя (44.11) в (44.3),(44.5) находим скорость и путь по часам на корабле
v = |
|
gt |
|
|
|
= c th gt |
, |
|||
|
|
|
|
|
|
|
||||
|
1 +g2t2 |
c2 |
|
c |
|
|||||
|
|
c |
2 |
æ |
|
gt |
|
ö |
|
|
|
|
|
ç |
|
|
÷ |
|
|||
|
x = |
|
|
çch |
|
|
|
÷ |
|
|
|
|
|
|
|
-1 . |
|
||||
|
|
g |
ç |
|
c |
|
÷ |
|
||
|
|
è |
|
|
ø |
|
||||
При gt c 1 |
x = c2 |
exp gt |
, |
|
||||||
|
|
|
|
2g |
|
|
|
c |
|
|
|
t = c ln |
2gx . |
|
|
||||||
|
|
|
|
g |
|
c2 |
|
|
||
(44.15)
(44.16)
(44.17)
(44.18)
Ниже приведена таблица движения для g 103 см/с |
(c/g 1 год). |
|||
|
|
|
|
|
t |
t |
v |
|
x |
1 год |
0.88 года |
0.7 с |
0.41 св. года |
|
10 лет |
3 года |
0.995с |
|
9.5 св. года |
1010 лет |
23 года |
» c |
|
1010 св. лет |
Последняя строка соответствует достижению видимого горизонта Вселенной (с более удаленных областей свет ещё до Земли еще не дошел). Космонавтам на это путешествие понадобится всего 23 года!
Расход горючего
Найдем, сколько потребуется топлива космическому кораблю. Вспомним сначала эту задачу для нерелятивистского случая. Ускорение ракете сообщают выброшенные назад продукты горения. Пусть их
скорость относительно ракеты равна u0 . Перейдем в систему ракеты. Из закона сохранения импульса (нерелятивистский случай)
m dv = dmгu0 , |
(44.19) |
где m – текущая масса ракеты, v – скорость ракеты, dmг |
– масса |
порции выброшенного газа, равная убыли массы ракеты -dm. Отсюда получаем уравнение
dm |
= -dv , |
(44.20) |
m |
u0 |
|
m = m0 exp(-v u0 ). |
(44.21) |
|
114

Это формула Мещерского-Циолковского, дающая связь между оставшейся массой ракеты и набранной скоростью.
Найдем теперь решение этой задачи в релятивистском случае. Перейдем в систему ракеты (S ¢ ). Из закона сохранения импульса при выбросе очередной порции "газов"
mdv¢ = dmгu 0gг, gг = 1 1 - u02 c2 . |
(44.22) |
Здесь считается, что скорость истечения газов может быть релятивистской, а изменение скорости ракеты в ее исходной системе мало и можно пользоваться нерелятивистскими выражениями. Из закона сохранения энергии находим
|
|
¢ 2 |
|
|
|
-d(mc2 ) = dm |
g c2 |
+m |
(dv ) |
. |
(44.23) |
|
|||||
г |
г |
2 |
|
|
|
|
|
|
|
||
Опуская последний член второго порядка малости, получаем
dmг г dm . |
(44.24) |
Подставляя (44.24) в (44.22), находим уравнение движения в системе ракеты
mdv¢ = -u0dm . |
(44.25) |
Заметим, что в системе ракеты релятивистское и нерелятивистское уравнения движения (44.25) и (44.19) совпадают.
Найдем связь между dv¢ и приращением скорости ракеты в неподвижной системе Земли. Для этого воспользуемся формулой преобразования скоростей (22.3)
|
|
|
|
V +dv¢ |
|
2 |
|
|
||
dvx |
» |
|
|
|
x |
|
-V » dvx¢(1 - |
V |
) . |
(44.26) |
1 |
¢ |
c |
2 |
2 |
||||||
|
|
+dvxV |
|
|
c |
|
||||
В нашем случае v º vx ºV , поэтому (44.26) можно переписать как
|
¢ |
|
|
dv |
|
|
|
dv |
= |
|
- |
v2 . |
(44.27) |
||
|
|
||||||
|
|
1 |
c2 |
|
|||
|
|
|
|
|
|
||
Подставляя dv¢ в (44.25), получаем
dm |
= - |
|
dv |
|
|
, |
(44.28) |
|
m |
u |
(1 -v2 |
c2 ) |
|||||
|
|
|
||||||
|
|
0 |
|
|
|
|
|
|
откуда
115

m |
æ |
1 -v c ÷öc 2u0 |
|
|||
ç |
|
÷ |
|
|||
|
|
= çç |
|
|
÷ . |
(44.29) |
m |
|
|
|
|||
0 |
ç1 |
+v c÷÷ |
|
|||
|
ç |
|
ø |
|
||
|
|
è |
|
|
||
Это и есть решение задачи Циолковского в общем случае.
(Интеграл в правой части (44.28) берется, используя разложе-
|
|
|
1 |
|
|
1 |
æ |
1 |
|
1 |
ö |
|
ние |
|
|
|
|
ç |
|
÷ |
, после чего интеграл легко берется.) |
||||
|
|
|
|
= |
|
ç |
|
- |
|
÷ |
||
|
|
|
|
|
|
|
||||||
|
1 |
-x |
2 |
|
2 |
ç |
|
|
|
÷ |
|
|
|
|
|
èx +1 x -1ø |
|
||||||||
Из полученной формулы видно, что самым экономичным является
фотонный двигатель. При u0 = c |
|
|
|
|
|
|||
|
m |
= |
|
1 |
-v c |
. |
(44.30) |
|
|
m |
|
1 |
|
||||
|
0 |
|
+v c |
|
||||
|
|
|
|
|
|
|
|
|
Последнюю формулу можно вывести более коротким способом. Заметим, что импульс ракеты равен импульсу фотонов, который связан с изменением полной энергии ракеты
p = |
Eg |
= |
m0c2 -E |
, |
(44.31) |
|
c |
c |
|||||
|
|
|
|
где E, p –энергия и импульс ракеты. Энергия и импульс ракеты
связаны соотношением (42.7) |
|
E2 - p2c2 = m2c4 . |
(44.32) |
Учитывая, что p = cE2 v , уравнения (44.31) и (44.32) можно переписать в виде
|
|
æ |
|
ö |
|
|
|
|
E |
ç |
|
v ÷ |
2 |
, |
|
(44.33) |
|
ç1 + |
÷ = m0c |
|
||||||
|
|
ç |
|
÷ |
|
|
|
|
|
|
è |
|
c ø |
|
|
|
|
E |
2 |
çæ |
- |
v2 ÷ö |
2 |
4 |
. |
(44.34) |
|
ç1 |
2 ÷÷ |
= m c |
|||||
|
|
ç |
|
÷ |
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
c ø |
|
|
|
|
|
Подставляя E из первого уравнения во второе, получаем искомое решение
m |
= |
|
1 |
-v c |
, |
(44.35) |
||
m |
0 |
1 |
+v c |
|||||
|
|
|
||||||
|
|
|
|
|
|
|
||
совпадающее с ранее полученным выражением (44.30).
116

Вернемся снова к движению равноускоренной ракеты, в которой мы хотели долететь до "горизонта". Пусть ракета имеет фотонный двигатель. Конечную массу ракеты можно найти подставив v из формулы (44.15) в (44.35), однако мы поступим иначе.
Импульс, уносимый порцией света в системе корабля
dpg¢ = dEg¢ c = -(dm)c |
(44.36) |
где dm – убыль массы корабля. Такой же импульс приобретет корабль в сопутствующей системе. Действующая на корабль cила
dp¢ |
|
(dm)c |
|
|
F ¢ = dt |
= mg = - |
|
, |
(44.37) |
dt |
||||
откуда |
|
|
|
|
m = m0 exp(-gt c). |
|
(44.38) |
||
Для путешествия до горизонта Вселенной с ускорением g потребуется 23 года в системе корабля (см. таблицу). Учитывая, что c/g = 1 год, получаем
m |
= e |
-23 |
. |
(44.39) |
m0 |
|
Если вначале ракета имела размер Земли (R = 6400 км), то в конце путешествия останется астероид радиусом 3 км!
Всю массу в фотоны просто так не превратишь, нужно столько же антивещества, чтобы получать фотоны путем аннигиляции, а антивещества нигде поблизости нет. Но почему бы не помечтать. Кстати, физики не просто мечтают, а могут подробно объяснить, что можно, а что нельзя, и почему.
§ 45. Упругие столкновения частиц
Все задачи на столкновения и распады решаются на основании закона сохранения 4-импульса.
В случае упругого столкновения двух частиц с массами m1 и m2 закон сохранения 4-импульса имеет вид
P1 +P1 = P2¢+ P2¢ , |
(45.1) |
здесь и далее большая буква P = {E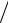 c, p} означает 4-импульс.
c, p} означает 4-импульс.
Уравнение, записанное в форме (45.1) является на самом деле четырьмя уравнениями. Однако, часто удобней оперировать с целыми
117
4-векторами. Для упрощения вычислений будем полагать с = 1. В конце вычислений всегда видно, где по размерности нужно добавить c.
Пусть две частицы сталкиваются навстречу друг другу с энергиями E1 и E2 и задан угол рассеяния первой частицы q . Нужно найти энер-
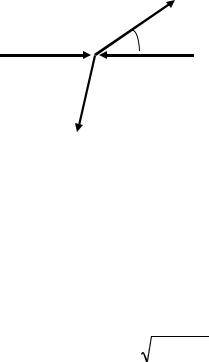
гию этой частицы. Параметры второй частицы после этого находятся простым вычитанием. В принципе, можно записать закон сохранения покомпонентно. Получится 3 уравне-
|
P1¢ |
ния (одно уравнение для сохранения |
|||
P1 |
q P2 |
импульса в направлении, перпендику- |
|||
лярном плоскости разлета, выпадает). |
|||||
|
|
Имеется |
также три |
неизвестных |
|
|
|
| p1¢ |, | p2¢ | |
и q2 , так что система одно- |
||
P ¢ |
|
значно разрешается. Однако эту задачу |
|||
2 |
|
можно решить проще. Исключим од- |
|||
|
|
||||
Рис. 35 |
|
ним шагом 2 неизвестные величины, |
|||
|
относящиеся ко второй частице |
||||
¢ 2 |
¢ 2 |
2 |
(c = 1) . |
(45.2) |
|
(P2 ) |
= (P1 |
+ P2 -P1 ) = m2 |
|||
После этого остается одно уравнение с одной неизвестной| p1¢ |,
которое легко решить.
Рассмотрим, для примера, рассеяние фотона на летящем навстречу электроне (эффект Комптона), рис. 35. Вначале электрон (летит справа) и гамма квант (слева) имели 4-импульсы
|
Pg = {Eg, pg, 0, 0}, |
Pe |
= {Ee,-pe, 0, 0} , |
(45.3) |
||||||
при этом| p |º p = |
E2 -m2 , |
| p |
g |
|= E |
g |
. |
|
|||
e |
e |
e |
|
|
|
|
|
|
||
В соответствии с (45.2) |
|
|
|
|
|
|
|
|
||
|
|
(P |
+P |
-P |
¢)2 |
= m2 |
(45.4) |
|||
|
|
e |
g |
g |
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
Pe2 |
+Pg2 + Pg¢2 |
+ 2PePg -2PePg¢ -2PgPg¢ = m2 . |
(45.5) |
|||||||
Учитывая, что(AB) = a0b0 - ab, |
, имеем |
|
||||||||
|
|
Pe2 = m2, Pg2 = Pg¢2 = 0 , |
(45.6) |
|||||||
|
PePg |
= EeEg + pe pg = Eg(Ee + pe ), |
(45.7) |
|||||||
|
|
PePg¢ = EeEg¢ + peEg¢ cos q, |
(45.8) |
|||||||
118

PgPg¢ = EgEg¢ -EgEg¢ cos q. |
(45.9) |
Подставляя эти выражения в (45.5) получаем |
|
Eg(Ee + pe ) -EeEg¢ - peEg¢ cos q -EgEg¢ + EgEg¢ cos q = 0 . |
(45.10) |
Откуда (возвращаем "с" на место) получаем энергию фотона после рассеяния
Eg¢ = Eg |
|
|
Ee + pec |
|
|
|
. |
|
E |
+ p c cos q + E |
g |
-E |
g |
cos q |
|||
|
e |
e |
|
|
|
|
||
Для покоящегося электрона
Eg¢ = Eg |
mc2 |
|
; l¢ = l +le(1 - cos J), |
|
mc2 + E |
(1 |
-cos J) |
||
|
g |
|
|
|
(45.11)
(45.12)
где le = /mc – комптоновская длина волны.
Рассмотрим интересный случай – «обратное комптоновское рассеяние» света лазера на ультрарелятивистском электроне Ee 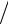 mc2 1,
mc2 1,
вблизи q = p (рассеяние лазерного фотона назад). В этом случае в числителе (45.11) можно положитьpec = Ee , а в знаменателе сделаем
замену p c |
= E2 -m2c4 » E - |
m2c4 |
|
, |
cos q » -1 + a2 |
, где |
||||||
|
||||||||||||
|
e |
e |
e |
2Ee |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|||||
a = p -q . Тогда ответ преобразуется к виду |
|
|||||||||||
|
|
Eg¢ = Ee |
x |
|
, где |
|
|
4EeEg |
(45.13) |
|||
|
|
|
|
x = |
|
. |
||||||
|
|
x +1 + a2g2 |
|
m2c4 |
||||||||
Например: |
Ee |
= 100 ГэВ, Eg = 2.5эВ (видимый свет), тогда x = 4 и |
||||||||||
при a = 0 |
получаем Eg¢ = 80 |
ГэВ, т.е. |
|
рассеянные назад |
фотоны, |
|||||||
летящие в направление исходных электронов, уносят 80 % начальной энергии электрона. Этот метод получения высокоэнергичных фотонов лежит в основе будущих фотон-фотонных коллайдеров на энергию
100-1000 ГэВ.
Если параметр x 1, то
Eg¢ = 4g2Eg, |
(45.14) |
что совпадает с формулой (42.17) для отражения света назад от движущегося зеркала.
119
§46. Распад частиц
1.Сначала рассмотрим распад покоящейся частицы с массой M на две частицы с массами m1 и m2 . Закон сохранения 4-импульса при та-
ком распаде имеет вид
P = P1 + P2 . |
(46.1) |
Из сохранения нулевой компоненты (энергии) следует, что распад возможен при (с = 1)
|
|
M = E1 + E2 |
> m1 +m2 . |
|
(46.2) |
|||||||||||
Найдем энергию первого осколка. Из (46.1) имеем |
|
|||||||||||||||
|
|
(P -P )2 = P |
2 = m2 . |
|
(46.3) |
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
2 |
|
|
|||
Учитывая, что P = {M,0}, P1 = {E1, p1 } |
, получаем |
|
||||||||||||||
|
|
M 2 -2ME |
1 |
+m2 |
= m2 , |
|
(46.4) |
|||||||||
откуда (возвращаем "с") |
|
|
|
|
|
|
|
1 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
M 2 |
+m2 |
-m2 |
|
(46.5) |
||||||
|
|
E |
|
= |
|
|
|
|
1 |
|
2 |
|
c2 |
|
||
|
|
1 |
|
|
|
2M |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и из симметрии (1 « 2) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
M 2 |
+m2 |
-m2 |
|
|
||||||
|
|
E |
|
|
= |
|
|
|
|
2 |
|
1 |
c2 . |
|
(46.6) |
|
|
|
2 |
|
|
|
2M |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это есть решение в системе покоя распадающейся частицы. |
|
|||||||||||||||
2. Пусть теперь первичная частица движется со скоростью V и при |
||||||||||||||||
распаде одна из конечных частиц с массой m1 |
º m имеет в системе |
|||||||||||||||
центра инерции (ц.и.) энергию E0 |
º E1 , импульс p0 = |
E02 -m2c4 |
||||||||||||||
(полученные выше) и скорость v0 |
= p0c / E0 . |
Найдем зависимость |
||||||||||||||
энергии данной частицы Е от угла q . |
|
|
|
|
|
|
||||||||||
Из преобразований 4-импульсов следует (с = 1) |
|
|||||||||||||||
E |
0 |
= g(E - pV cos J), |
|
где |
p = |
E2 -m2 . |
(46.7) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда для E получается квадратное уравнение |
|
|
||||||||||||||
E2(1 -V 2 cos2 q) -2EE0 1 -V 2 +E02(1 -V 2 ) +V 2m2 cos2 q = 0 |
(46.8) |
|||||||||||||||
Из геометрических соображений (также как и в случае нерелятивистского распада, рис. 26) ясно, что если v0 <V , то одному углу соот-
ветствует два решения.
120
