telnov-machanika-and-TO

Рассмотрим движение тела вдоль спицы вращающего колеса. Мо-

мент инерции тела L = mwr2 увеличивается при движении от центра. Изменение момента импульса за единицу времени равно моменту сил

Эта сила, с которой спица действует на тело, сопротивляясь силе Кориолиса. Поскольку сила Кориолиса перпендикулярна угловой скорости и скорости тела, то в векторном виде ее можно записать как

Далее мы получим это выражение строго математически.

Рассмотрим снова рис. 83. Система S является неподвижной, а система S ¢ движется относительно ее как поступательно, так и вращательно. Скорость материальной точки относительно неподвижной системы

где v0 поступательная скорость начала отсчета системы S ¢ , [ω× r] –

скорость, связанная с вращение системы S ¢ (как для твердого тела), vотн – скорость точки относительно начала отсчета системы S ¢ . Дейст-

вительно

231

находим

центробежное

Рассмотрим смысл каждого члена.

aабс = F/m – это ускорение, вызванное реальной силой;

a0 +[ω× r] +[ω×[ω× r]] – переносное ускорение, связанное с движением системы S ¢ ;

2[ω× vотн ] – ускорение Кориолиса.

Член [[ω× r]×ω] в переносном ускорении – это центробежное ускорение. Полагая r = r + r^ (относительно ω), находим

Перегруппировав члены в (91.14) с учетом (91.15), получим уравнение относительного движения

Примеры силы Кориолиса:

Маятник Фуко – это обычный тяжелый маятник на длинном подвесе. Впервые публичная демонстрация была осуществлена Фуко в 1851 г. в Парижском Пантеоне. Плоскость колебаний такого маятника повора-

232

верхности Земли. Составляющая угловой скорости параллельная поверхности Земли не влияет, т.к. создает силу вдоль троса. Период вращения плоскости колебаний

На рис. 87 показаны фигуры, описываемые нижним концом маятника, если его оттянуть и опустить (слева) и толкнуть из центра (справа).

Подмывание берегов

В северном полушарии сила Кориолиса направлена вправо от направления движения, поэтому правые берега рек в Северном полушарии более крутые – их подмывает вода. В Южном полушарии всё происходит наоборот.

Колеса поезда

Правые колеса (в северном полушарии) поезда сильнее прижимаются к рельсу сбоку и быстрее снашивается.

Ураганы

Ураганы закручиваются силой Кориолиса. Наиболее сильные на сороковых «ревущих» широтах. На экваторе не бывает.

§92. Приливы

Уберегов морей и океанов дважды в сутки наблюдается подъем уровня воды до некого максимального значения и столько же раз опускание до минимального уровня. Они являются результатом изменения положений Луны и Солнца относительно Земли совместно с эффектами вращения Земли и особенностями рельефа. В некоторых местах подъем достигает 10-15 м, но в среднем перепад составляет порядка одного метра. Аномальные подъемы связаны с увеличением высоты волны при набегании ее на берег и геометрией береговой линии.

233

C

O

Рис. 88

Рассмотрим механизм возникновения приливной волны в идеализированном случае, когда имеется сплошной океан. Приливные силы зависят не от величины гравитационного поля (Луны, Солнца), а от степени его неоднородности (градиента). Ниже будет получено соотношение приливных эффектов от Луны и Солнца. Пусть для определенности Луна притягивает Землю, рис.88. Рассмотрим ускорения, действующие в точках А, B и С, вычитая при этом ускорение центра масс Земли.

Поскольку точка А ближе у Луне, то в ней дополнительная гравитационная сила направлена к Луне, в то время как в противоположной точке В сила такая же, но направлена от Луны. В точке C имеется составляющая перпендикулярная линии, соединяющей Луну и Землю. Приливы в точках А и В будут происходить одновременно и одинаковой величины.

Ускорение в точке находящейся между О и А на расстоянии x от центра Земли за вычетом ускорения центра Земли равно

Потенциал в точке А относительно О, связанный с этим градиентным полем,

Потенциал между точками С и О может быть найден непосредственно как разность потенциалов в этих точках, поскольку в этом направлении центр масс Земли не имеет ускорения.

234

Отсюда разность эффективная разность потенциалов между А и С (эффективная потому, что вычтено поле, действующее на ц.м. Земли) равна

Эта разность потенциалов равна gh , где h разность уровней подъема воды в точках А относительно точки С, g – ускорение свободного па-

дения на поверхности Земли. Учитывая, что g = GMЗ находим пере-

RЗ2

пад подъемов воды при приливах, связанный с Луной,

3M R4

hЛ = 2r3 ЛMЗ » 0.55 м. (92.5)

ЛЗ З

Ответ для прилива за счет Солнца находится заменой MЛ MС ,

rЛЗ rСЗ :

3M R4

h С = 2r3 СMЗ ~ 0.24 м. (92.6)

СЗ З

Выше была рассмотрена статическая теория приливов, в которой горбы на воде появляются на линии Луна-Земля (средневзвешенным направлением между Луной-Солнцем и Землей). Более точная, динамическая теория учитывает движение приливной волны вокруг Земли. Не вдаваясь в детали можно сказать, что приливные силы можно считать вынуждающей силой, а период обхода волны вокруг Земли собствен-

Луна

Динамическая

Рис. 89

ной частотой осциллятора. Период обхода волны вокруг Земли оказывается больше периода вынуждающей силы. В этом случае, в соответ-

235

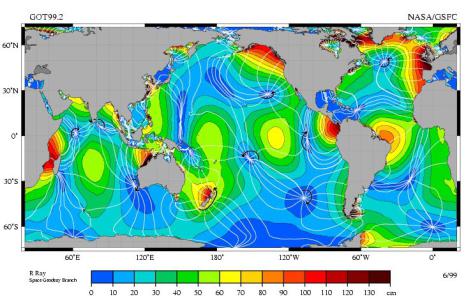
Рис. 90

ствие с теорией вынужденных колебаний осциллятора с малым затуханием (§ 57), амплитуда отстает от силы на p , т.е. на половину периода. Это приводит к тому, что горбы на воде будут находиться прямо противоположно тому, что предсказывает статическая теория (минимумы вместо максимумов и наоборот), рис 89.

Реально, наличие материков меняет эту картину до неузнаваемости, рис. 90. Точно только, что приливы происходят дважды в сутки, но высота зависит от места и может отличаться от наших расчетов в несколько раз в большую или меньшую сторону.

236

Г Л А В А XII

ГРАВИТАЦИЯ, ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

§ 93. Введение

Ранее мы рассмотрели Специальную Теорию Относительности (СТО), которая описывает движение тел относительно инерциальных систем отсчета. При этом предполагалось, что пространство евклидово и сигналы связи, например, свет, распространяются по прямым линиям. При известном законе взаимодействия СТО, в принципе, позволяет рассчитать все движения тел при любых скоростях.

В таком подходе, однако, имеются проблемы при рассмотрении гравитационных взаимодействий. Силы гравитации действуют на все тела без исключения, в том числе и на свет. Траектории фотонов становятся "кривыми", и само пространство становится искривленным. Еще одна особенность – гравитационные поля создаются не только самими телами, но и любым видом энергии (в том числе гравитационной). Принцип суперпозиции в достаточно сильных гравитационных полях не выполняется.

Явления, связанные с гравитацией, описывает Общая Теория Относительности (ОТО), созданная А. Эйнштейном (1916). Принцип относительности был распространен на системы, находящиеся в гравитационных полях. Ключом к решению задачи стал принцип эквивалентности. Гравитационные поля по своему действию очень похожи на силы, возникающие в неинерциальных (ускоренных) системах отсчета. В падающем лифте сила инерции и гравитационная сила компенсируются. Законы физики в такой системе будут совпадать с законами в инерциальных системах. Сидя в лифте нельзя сказать, какая часть силы вызвана гравитацией, а какая ускорением лифта. Разница заключается только в том, что силы инерции можно полностью исключить выбором системы отсчета, а истинно гравитационные силы можно скомпенсировать силами инерции только в точке. Так в падающем лифте пробное тело, помещенное в центре лифта, будет иметь нулевое ускорение относительно лифта, в верхней точке лифта сила тяжести немного меньше, поэтому тело будет ускоряться вверх, соответственно в нижней точке вниз.

237

Еще один принципиально важный момент. Пусть наблюдатель на вращающемся диске разложил вдоль радиуса и обода короткие одинаковые линейки. Какое он получит отношение длины периметра к радиусу? Ответ на этот вопрос проще всего найти, взглянув на эту картину из неподвижной инерциальной системы отсчета. Линейка, лежащая на диске вдоль радиуса, будет иметь одинаковую длину в системе диска и в неподвижной системе отсчета, т.к. поперечные размеры при движении не изменяются. Однако, линейка, лежащая вдоль обода на вращающемся диске, будет в неподвижной системе отсчета в

рый в неподвижной системе отсчета имеет длину 2pR , можно уложить движущихся линеек в g раз больше, чем в случае покоящегося диска.

Число линеек, лежащее на диске, не зависит от системы отсчета, следовательно, наблюдатель на диске получит отношение длины обода к радиусу равное 2pg . Это означает, что геометрия на вращающемся

диске отличается от евклидовой! Инерциальные силы искривляют пространство. К таким же эффектам приводит и истинная гравитация. Кривизна пространства является неотъемлемой составляющей Общей теории относительности.

Примером искривленного двумерного пространства является поверхность сферы. Говоря о ее кривизне, мы обычно воображаем сферу, помещенную в трехмерное пространство. Реально, наблюдатель, живущий в n-мерном мире, не может выбраться в n+1 –мерное пространство, чтобы увидеть кривизну своего пространства. Однако он может определить геометрию своего пространства, измерив сумму углов в треугольнике. Для окружности на сфере отношение периметра к радиусу будет меньше 2p. На вращающемся диске это отношение было больше 2p. Если вместо вращающегося диска, на котором центробежные силы направлены от центра, рассмотреть пространство вокруг массивного тела, то там отношение периметра к радиусу будем меньше 2p, как на выпуклой сфере.

Математический аппарат Общей теории относительности довольно сложен. ОТО пользуются в основном астрономы и космологи. Ее использование необходимо при рассмотрении эффектов вблизи компактных объектов, таких как нейтронные звезды и черные дыры, а так же для описания динамики расширяющейся Вселенной. Имеется ряд эффектов, предсказанных Общей теорией относительности и проверен-

238

ных экспериментально. Пока не найдено ни одного эффекта, противоречащего ОТО.

Хотя закон Кулона для электрических взаимодействий совпадает с законом тяготения Ньютона, хорошо описывающего гравитационные взаимодействия при слабых полях и небольших скоростях ( в обоих

случаях F µ 1/r2 ), эти два типа взаимодействий принципиально раз-

личные. Они отличаются не только тем, что у них различные константы взаимодействия, у них переносчики взаимодействия имеют разные спины (внутренние моменты импульсов), сила взаимодействия поразному зависит от скорости частиц. Эти непростые вопросы и здесь их обсуждать не будем, рассмотрим только несколько явлений, для объяснения которых достаточно принципа эквивалентности.

§ 94. Инертная и гравитационная масса, принцип эквивалентности

Масса, входящая во второй закон Ньютона, характеризует инертность тела и называется инертной массой

В законе всемирного тяготения сила притяжения пропорциональна произведению гравитационных масс

Оказывается, что с огромной точностью инертные массы пропорциональны гравитационным. Именно поэтому имеет место принцип эквивалентности, о котором мы говорили во Введении. Как это можно проверить? Рассмотрим падение двух тел 1 и 2 в поле тяжести Земли. Ускорения тел находятся из соотношений

где mi, mg – инертная и гравитационная масса пробных тел, М – гравитационная масса Земли. Отсюда находим

239

Галилей первым заметил, что все тела в пустоте падают с одинаковым ускорением: a (2)= a(1) и, следовательно,

Если это отношение одно и то же для всех тел, то путем выбора значения гравитационной постоянной это отношение можно сделать равным единице, т.е. считать гравитационную массу равной инертной.

В отличие от Галилея Ньютон использовал для проверки этого утверждения маятник, период которого

Из этого опыта следует равенство mi и mg для различных тел с точно-

стью 10-5 .

Большая точность достигается в статических экспериментах. Если на тело действует две силы, одна пропорциональная mi , а другая mg ,

то направление результирующей силы зависит от mi/mg . Такая уста-

новка создана самой природой. Земля вращается вокруг оси и является неинерциальной системой отсчета. На тело, покоящееся относительно Земли, действуют две силы: гравитационное притяжение, пропорцио-

нальное mg , и центробежная сила, пропорциональная mi .

В 1890-1920 годах Этвеш провел основанные на этом принципе эксперименты, используя крутильные весы с подвешенными на коромысле гирями из различных материалов, но с одинаковыми гравитационными массами (коромысло параллельно Земле), рис. 91. Если инертные массы этих гирь, сделанных из разных веществ, были бы не равны, то за счет центробежных сил коромысло получило бы крутильный момент. Действительно, коромысло уравновешенно в вертикальной плоскости при

Вращающий момент в горизонтальной плоскости

240