telnov-machanika-and-TO

Границы области движения по радиусу соответствуют r = 0 в (69.14), т.е. r находится из уравнения

Если имеется две границы rmin и rmax , то движение называется финитным (ограниченным). Угол поворота при движении от rmin до rmax и обратно

Траектория замкнута, если Dj = 2p nk , где k,n - целые числа (траек-

тория замыкается после n колебаний по радиусу и k полных оборотов по j). В общем случае траектория незамкнута. Оказывается, она замк-

Поскольку E – конечная величина, но последний член в выражении равен нулю. Отсюда следуют условия падения на центр

.

171

В слабом гравитационном поле U µ -r1 , поэтому частицы не па-

дают на центр, однако в сильном гравитационном поле (вблизи черных дыр) в потенциале появляются члены более высокой степени

U µ -ar - rb2 ..., что приводит к падению материи на центр тяготения.

Примеры эффективного потенциала

1) Притягивающий кулоновский (гравитационный) потенциал

2) Пространственный осциллятор

Пространственный осциллятор – это тело на пружинке, которое может не только колебаться вдоль пружинки, но и вращаться вокруг закрепленного конца. В этом случае

Движение финитно при любой физически возможной энергии.

rmin

rmin rmax

Рис. 50

172

Движение по круговым орбитам

Это получается как из приравнивания ускорения вызванного силой ус-

Казалось бы, все просто, при каждом радиусе найдется скорость, необходимая для кругового движения. Но будет ли это движение устойчиво? Движение устойчиво, когда на круговой орбите эффективный потенциал имеет минимум, и неустойчиво (падение на центр) когда в

этой точке Uэф имеет максимум.

Условия устойчивости движения аналогично условиям падения на центр, рассмотренным ранее:

При устойчивом движении небольшой радиальный толчок тела приведет к колебаниям вблизи исходной круговой орбиты, например, при n = 1 окружность превращается в эллипс.

Гравитационный потенциал удовлетворяет условию (69.30), а пространственный осциллятор условию (69.31). Однако, если потенциал

U(r) = -ra10 , то тело будет двигаться по окружности, но неустойчиво.

Малейшее начальное радиальное движение будет нарастать, и тело упадет на центр или улетит на бесконечность.

173

§ 70. Кеплерова задача

Немецкий математик и астроном Кеплер (1571-1630) из анализа данных датского астронома Тихо Браге (1546-1601) установил три эмпирических закона:

1)Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

2)Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

3)Квадраты периодов обращения планет вокруг Солнца относятся, как

Задача о круговом движении в гравитационном поле довольно простая и еще до Ньютона было известно, что, если F µ -r12 , то получа-

ются законы Кеплера. Исаак Ньютон (1642-1727) математически показал, что, действительно, при F µ -r12 планеты движутся по эллипсам

и при этом выполняется третий закон Кеплера. Рассмотрим эту задачу.

Траектория движения

Итак, имеем

где последнее соотношение соответствует круговому движению. Из (69.18) получаем

174

Выбором начала отсчета делаем const = 0 . Отсюда траектория движения

Это кривые, соответствующие коническим сечениям (кривые, по которым поверхность круглого конуса пересекается плоскостью, см. курс аналитической геометрии). Величины p и e называются

параметром и эксцентриситетом орбиты.

В аналитической геометрии показывается, что при e = 0 – это круг;

e < 1 – эллипс (E < 0 -финитная траектория); e = 1– парабола (E = 0 );

175

e > 1 – гипербола (E > 0 ).

Рассмотрим случай эллиптической траектории. Как известно, у эллипса имеется два фокуса, и сумма расстояний от фокусов до любой

(при финитном движении энергия отрицательна, поэтому здесь использован модуль E , чтобы знак минус не вводил в заблуждение),

отсюда

176

Как мы видим, большая полуось a зависит только от полной энергии, а малая полуось зависит также от момента импульса.

Заметим, что выражение для rmax,rmin и a легко получить из законов

сохранения энергии и момента импульса. Действительно, в перигелии и афелии нет радиального движения, тогда

что совпадает с (70.8) и (70.9).

Период обращения

Из сохранения момента импульса

где T – период обращения. Учитывая, что для эллипса S = pab получаем

Этот закон легко получить в случае кругового движения, но оказывается формула остается справедливой и для эллиптического движения, если вместо радиуса в формуле использовать большую полуось эллипса. Для гравитационного взаимодействия тел с массами M и m подставляем

177

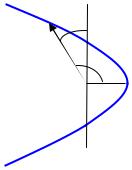
Случай e > 1, E > 0 , — гипербола

Гипербола – геометрическое место точек, для которых абсолютная величина разности расстояний до двух заданных точек (фокусов) (-c, 0),

(c, 0)постоянна и равна 2a < 2c . Уравнение гиперболы в декартовых координатах

тории при пролете мимо центра тяготения, см. рис. 52,

178

параметр (расстояние между продолжением исходной траектории и центром тяготения) r, то подставляя в (70.25)

Случай отталкивающего потенциала

Пусть

После вычислений аналогичных (70.2) получается уравнение траектории, отличающееся от (70.4) только знаком минус перед единицей

179

Из сравнения (70.31) и (70.25) следует, что углы отклонения для притягивающего и отталкивающего потенциалов одинаковы! Это весьма неочевидный результат. Половинный угол поворота для частицы, летящей с бесконечности, будет даваться той же формулой (70.27). Разница только в том, что в случае притяжения частица отклоняется в сторону центра притяжения, а в случае отталкивания в обратную сторону.

Конические сечения.

Выше было декларировано, что формула (70.4) описывает эллипсы, параболы, гиперболы. Покажем это. Учитывая, что cos x / r , запи-

шем (70.4) в виде

Далее, после перегруппировки членов получается

1) e 1 (эллипс)

180