telnov-machanika-and-TO

ной массой с относительной скоростью, равной начальной относительной скорости частиц, т.е.v1 . Записываем уравнения сохранения момен-

та импульса и энергии для начального положения и расстояния минимального сближения d

Подставляя v из первого уравнения во второе, находим ответ задачи

Поскольку расстояние не может быть отрицательным, перед корнем нужно взять знак плюс.

Сечение рассеяния (сечение реакции) – это очень широко используемые характеристики в атомной физике и физике элементарных частиц. Для их расчетов используется квантовая механика, и сечения процессов уже нельзя представлять чисто геометрически, но по-прежнему вероятность рассеяния (или процесса рождения новых частиц) дается формулой dp = nxds .

201

Г Л А В А IX

ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

§ 80. Твердое тело, система координат, угловая скорость, ось вращения

До сих пор рассматривалась, в основном, кинематика и динамика поступательного движения. Кинематика вращательного движения твердого тела обсуждалась кратко в § 11, где было введено понятие угловой скорости, найдено перемещение и скорость точек при вращении тела вокруг оси. Также при рассмотрении законов движения был введен момент импульса системы, и было показано, что для замкнутой системы он сохраняется вследствие третьего закона Ньютона (поскольку сумма моментов внутренних сил равна нулю). Было показано также, что сохранение момента импульса обусловлено изотропностью пространства.

При дальнейшем рассмотрении динамики вращательного движения мы увидим, что имеется много аналогий между динамикой поступательного и вращательного движения: закон сохранения импульса p и

закон сохранения момента импульса L ; поступательная скорость v и угловая скорость ω, импульс p = mv и момент импульса L = I ω, где

I – момент инерции; кинетические энергии K = mv2 2 и K = I w2 2 , за-

коны движения ddtp = F и ddtL = τ, где τ – момент сил. Однако, в об-

щем случае, рассмотрение вращательного движения является более сложной задачей, поскольку момент инерции зависит от формы тела. Это приводит, например, к тому, что вектор угловой скорости может не совпадать с вектором момента импульса и менять направление в пространстве даже в отсутствие внешних сил.

Далее мы проанализируем общие законы движения твердого тела, но конкретное рассмотрение проведем только для достаточно простых случаев. Более детально движения твердого тела будет изучаться в курсе аналитической механика.

Твердое тело – система материальных точек, расстояния между которыми неизменно. Движение будем описывать с помощью двух систем отсчета: инерциальной системы XYZ и системы координат

202

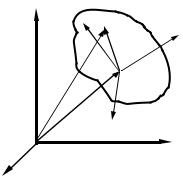
x1,x2,x3 (или x,y,z ), жестко связанной с телом и участвующей во всех

его движениях. Для задания положения тела в неподвижной системе отсчета необходимо задание 6 чисел, три координаты для задания начала отсчета подвижной системы и три угла для ориентации ее осей относительно неподвижной системы, т.е. твердое тело имеет 6 степеней свободы.

где V – поступательная скорость тела, ω– угловая скорость. При чисто поступательном движении линия между двумя произвольными точками на теле перемещается параллельно самой себе; при чисто вращательном тело совершает движение вокруг некоторого направления.

Пока мы не делали никаких предположений о выборе центра подвижной системы. Пусть центр подвижной системы сдвинули на вектор

a , так что r = a + r¢. Подставляя в (80.3), получаем

отсюда

203

Таким образом, угловая скорость не зависит от выбора начала отсчета, скорость же поступательного движения такого абсолютного характера не имеет. Центр подвижной системы отсчета является как бы мгновенной осью вращения, а полная скорость произвольной точки на теле есть сумма скоростей этого центра и вращательной скорости точки (относительно этого центра).

В некоторых случаях выбором a можно сделать V¢ = 0 . Тогда все движение будет сводиться к вращению относительно мгновенного центра вращения. Из (80.6) следует, что для этого необходимо V ^ ω.

Для вращений имеет место закон сложения угловых скоростей. Действительно, вместо одновременного вращения с двумя угловыми скоростями, совершим два последовательных малых поворота за равные

времена, сначала с угловой скоростью 1 , затем с ω2 . Изменение радиус вектора при первом повороте dr1 = [ω1 × r]dt , при втором повороте dr2 = [ω2 ×(r + dr1 ]dt » [ω2 × r]dt (отброшен малый член второго порядка). Откуда dr = dr1 +dr2 = [ω× r]dt , где ω = ω1 + ω2 .

Примеры:

1)Колесо катится по дороге со скоростью V. Нижняя точка является мгновенной осью вращения. Центр колеса движется со скоростью V, а верхняя точка колеса, со скоростью 2V.

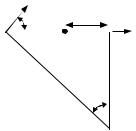
2)Левый конец палки длины L имеет мгновенную скорость VA под уг-

aложение мгновенной оси вращения (точка О).

204

§ 81. Кинетическая энергия и момент импульса вращающегося тела

Кинетическая энергия тела

Кинетическая энергия тела в неподвижной системе координат

åmV[ω× r] = åm r[V ×ω]. Тогда, если начало отсчета подвижной

системы координат помещено в центре масс тела, то второй член равен нулю, поскольку åm r = 0 . В результате получаем, что кинетическая

энергия тела есть сумма энергии поступательного движения тела как целого (M = åm ) и вращательной энергии

sin2 q 1 -cos2 q .

Напомним, что координаты частиц здесь даются в системе координат жестко привязанной к телу и вращающейся вместе с ним. Угловая скорость также определена относительно подвижной системе координат и в общем случае изменяется по направлению и величине (постоянным является момент импульса).

205

Рассмотрим сначала простейший случай, когда угловая скорость постоянна, например, тело вращается на закрепленной оси. Тогда точ-

ки тела движутся вокруг оси на расстояниях ri = ri sin qi со скоростями v^ = riw , тогда выражение для кинетической энергии приобретает простой и понятный вид

Величина I называется моментом инерции тела относительно оси.

Момент импульса тела

Найдем момент импульса вращающегося тела в неподвижной системе отсчета. По определению

Если начало отсчета подвижной системы, прикрепленной к телу, отсчитывается от центра масс тела, то åmr = 0 , поэтому второй и тре-

тий члены равны нулю. В результате получаем

Отсюда видим, что момент импульса есть сумма момента импульса, связанного с поступательным движением, и момента импульса вращательного движения. Если импульс тела равен нулю, то момент импуль-

са не зависит от начала отсчета.

Далее будем считать, что центр масс тела покоится. Используя пра-

Это есть общее выражение для момента импульса тела относительно центра масс тела (точки). Во-первых, замечаем, что направления момента импульса и угловой скорости в общем случае не совпадают. Возьмем, например, гантели, у которой одна масса m расположена в

206

точке r , а вторая масса в точке -r , при этом направление вектора r имеет угол q по отношению к угловой скорости. В соответствие с

(81.9) полный момент импульса L = 2mr2 sin q и направлен ^ r , откуда видно, что направления угловой скорости и момента импульса отличаются.

При вращении тела вокруг закрепленной оси направления L и ω также могут не совпадать, как в рассмотренном выше примере. Кроме того, направление L может не сохраняться, т.к. подшипники могут давить на ось в боковом направлении, создавая момент сил, изменяющий момент импульса (это и будет происходить в рассмотренном примере). Однако, при вращении тела вокруг оси сохраняется проекция момента импульса на направление угловой скорости. Действительно, если сила действует на ось перпендикулярно оси, то создаваемый ей момент сил в направлении оси вращения (пусть это ось Z ) равен нулю (т.к. плечо равно нулю). Момент импульса вдоль оси меняться только за счет сил трения, действующих по касательной к оси. Чтобы они создавали меньший момент сил, ось в месте закрепления обычно делают как можно тоньше.

Итак, при вращении тела, закрепленного на оси направленной вдоль Z , сохраняется проекция момента импульса

где r2 = x2 +y2 – расстояние точки до оси вращения. Это следует непосредственно из (81.9), действительно

Lz = åm(wzr2 - wzz2 ) = åm wz (x2 +y2 ).

Сравнивая общие выражения для кинетической энергии вращения (81.3) и момента импульса (81.9), нетрудно заметить, что

§ 82. Главные оси вращения, главные моменты инерции тела

Проанализируем выражение для момента импульса тела (81.9). Компонента момента импульса вдоль оси x («прибитой» к телу)

207

L = åm(w r2 -x(rω)) =

=wx åm(y2 +z2 ) - wy åmxy - wz åmxz . (82.1)

Внего дают вклады не только угловая скорость wx , но и угловые ско-x x

рости вдоль осей y и z. Аналогичная ситуация и для других проекций. Всего возникает три типа добавочных членов: åmxy , åmxz и

åmyz . Оказывается, можно так направить три взаимно-

перпендикулярные оси координат, привязанные к телу, чтобы все эти добавочные члены занулились. Такие оси называются главными осями инерции. Действительно, направление подвижной системы координат задается тремя числами и, поэтому неудивительно, что варьируя их можно сделать нулевыми три суммы чисел, зависящие от этих направлений. Более подробно это будет обсуждаться в курсе аналитической механики.

В системе главных осей инерции в выражении (82.1) остается только первый член и выражения для компонент момента импульса приобретают вид

Моменты инерции относительно главных осей, проходящих через центр масс, называются центральными главными моментами инерции тела. Учитывая (81.11) и (82.5), кинетической энергии в системе главных осях имеет вид

208

Как видно из (82.2)-(82.4), главные моменты инерции равны сумме произведений масс составляющих тело на их расстояние до соответст-

вующей оси в квадрате: Ii = åmr2 (или ò r2dm) .

Нетрудно видеть, что сумма любых двух моментов инерции больше третьего, так

I1 +I2 = åm(x12 +x22 +2x32 ) > åm(x12 + x22 ) = I3 . (82.7)

Тела можно классифицировать следующим образом: I1 ¹ I2 ¹ I3 – асимметрический волчок;

I1 = I2 ¹ I3 – симметрический волчок;

I1 = I2 = I3 – шаровой волчок.

При вращении вокруг главных осей направление угловой скорости совпадает с направлением момента импульса и сохраняется. При этом оказывается, что вращение относительно главных осей с максимальным и минимальным моментом инерции устойчиво, а относительно среднего по величине неустойчиво, в чем легко убедиться с помощью спичечного коробка.

Нахождение главных осей для тела является непростой задачей, однако часто их направление очевидно из соображений симметрии. Например, для прямоугольного параллелепипеда главные оси проходят перпендикулярно граням через центр тяжести. Для круглого цилиндра

– оси проходят вдоль цилиндра и поперек через ц.м..

Плоское тело, x3 = 0 , имеем

I1 = åmx22, I2 = åmx12, I3 = åm(x12 + x22 ), т.е. I3 = I1 + I2 . (82.8)

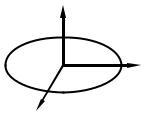
Найдем моменты инерции для круглой тонкой пластинки. Момент от-

1

Рис. 66

209

где r – плотность на единицу площади, интегрирование идет по кольцам. Поскольку из симметрии I1 = I2 , то из (82.7) следует

§ 83. Теорема Гюйгенса-Штейнера

Пусть момент инерции тела относительно, оси проходящей через центр, масс равен I0 . Момент инерции относительно оси сдвинутой

параллельно на расстояние a

Поскольку, по определенью, при расположении начала отсчета в центре масс årdm = 0 , то

Эта формула Гюйгенса-Штейнера.

Данный результат можно получить еще по-другому. Кинетическая энергия (81.2)

Полагая V = wa , получаем K = I w2 2 , где I = Ma2 + I0 , что совпада-

ет с (83.2).

Моменты инерции некоторых тел

Тонкий стержень (палка)

Момент инерции относительно центра палки

тогда, используя теорему Гюйгенса-Штейнера, находим момент инерции относительно конца палки

210