
telnov-machanika-and-TO
.pdfменения параметров могут возникать параметрический резонанс. Рассмотрим такой резонанс на частном примере, обычных качелях.
При раскачке качелей мы внизу встаем, а в верхней точке приседаем. В верхней точке качели покоятся, и приседание на их движение не влияет (только меняется на мгновение натяжение веревок). В нижней точке встаем на dl , при длине качелей l . Из сохранения момента импульса
|
vl |
æ |
ö |
|
|
ç |
dl ÷ |
|
|
v + dv = |
|
» v ç1 + |
÷. |
(58.1) |
|
||||
|
l -dl |
ç |
÷ |
|
|
è |
l ø |
|
Найдем изменение энергии. В нижней точке потенциальная энергия равна нулю, поэтому
E = mv2 |
, |
dE = mvdv = mv2 dl |
= 2E dl . |
(58.2) |
2 |
|
l |
l |
|
Это есть приращение энергии за одно вставание. С учетом того, что за один период качели проходят нижнюю точку дважды, то число вставаний за время dt будет
|
dN = |
2dt |
, |
|
|
|
|
|
(58.3) |
|
T |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
отсюда |
dE = |
4dl dt |
= 4 |
w0 |
dl dt , |
(58.4) |
|||
l |
T |
|
|||||||
|
E |
|
|
2p l |
|
||||
|
E = E0 exp( |
2w0 |
dl |
t) . |
(58.5) |
||||
|
p |
l |
|||||||
|
|
|
|
|
|
|
|||
Энергия качелей растет, потому что при вставании в нижней точке совершается большая работа, чем возвращается при приседании в верх-
ней точке, в виду дополнительной прижимающей вниз силы mv2/l .
Поскольку есть затухание E = E0e-2gt , то для роста амплитуды нужно
2w0 |
dl |
> 2g или |
dl |
> gp |
= |
p |
. |
(58.6) |
|
p |
l |
|
l |
w |
0 |
|
2Q |
|
|
|
|
|
|
|
|
|
|
|
|
§ 59. Адиабатический инвариант
151

Рассмотрим следующую задачу. Пусть маленький шарик летает между неподвижной стенкой и тяжелой пластиной удаляющейся от стенки со скоростью u , упруго отражаясь от них. При этом пластина движется очень медленно, так что за один период движения шарика относительное изменении расстояния между стенкой и пластиной мало. На фазовой плоскости шарик описывает траекторию, показанную на рис. 43 сплошной линией. Через много периодов движения фазовая траектория изменится, как схематично показано пунктирной линией. Как меняется площадь S внутри фазовой кривой?
Поскольку S = xv, то ее изменение |
|
DS = vDx + xDv . |
(59.1) |
Изменение модуля скорости шарика при упругом отскакивании от
стенки, удаляющейся со скоростью u , равно |
|
Dv = -2u . |
(59.2) |
Это следует из того, что в системе стенки шарик до столкновения имеет скорость v -u , которая меняется на противоположную при отскакивании. При переходе в неподвижную систему от этой скорости нужно отнять скорость стенки, в результате, скорость шарика после отскока будет v -2u . Изменения расстояния пластины от стенки за один период движения шарика
Dx = uT = u |
2x |
. |
(59.3) |
|
|||
|
v |
|
|
Подставляя (59.2),(59.3) в (59.1), получаем |
|
||
DS = v u 2x -x 2u = 0 . |
(59.4) |
||
v |
|
||
Итак, при медленном, адиабатическом, изменении параметров системы (расстоянии между стенкой и пластиной) фазовая кривая остается (почти) замкнутой, ее форма меняется, но площадь остается постоян-
ной, является адиабатическим инва-
|
X |
|
риантом. |
|
|
|
|
v |
|
|
Найдем |
теперь |
сохраняющуюся |
||
|
|
||||||
|
|
|
величину при медленном изменении |
||||
|
|
|
параметров (жесткости) гармониче- |
||||
|
|
|
ского осциллятора. |
|
|
||
|
|
|
X |
mx2 |
kx |
2 |
|
|
|
x |
|
||||
|
Рис. 43 |
|
Имеем E = |
2 |
+ |
2 |
, где k мед- |
152

ленно меняется. Продифференцируем и произведем усреднение по большому времени (значков усреднения не пишем, но подразумеваем)
|
|
|
|
2 |
|
2xx |
+ 2mxx = |
|
2 |
|
|
|
|
|
|
E |
|
|
E |
= |
kx |
|
+k |
kx |
|
+ x (kx +mx) |
= k |
|
|
.(59.5) |
|||||||
|
|
|
2 |
|
2 |
|
||||||||||||
|
|
|
2 |
2 |
2 |
|
|
|
|
k |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Отсюда для средней энергии получаем |
|
|
|
|
|
|
|
|
|
|
|
|||||||
dE = |
1 dk |
ln E = |
1 lnk+const |
|
E |
= |
E |
= const , |
|
(59.6) |
||||||||
|
|
|
|
|
||||||||||||||
E |
2 k |
|
|
|
|
2 |
|
|
|
k |
|
w0 |
|
|
|
|
||
где w0 = k/m , m считается постоянной. В случае математического маятника (шарик на нитке), w02 = g/l , значит, инвариантом является величина I = E l/g . При уменьшении длины нитки энергия возрастает, поскольку совершается работа больше, чем mgDl
Итак, при медленном изменении параметров осциллятора инвариантом является величина
|
|
I = |
E |
. |
|
|
|
|
(59.7) |
|
|
|
|
|
|
|
|||||
|
|
|
w |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mw2x2 |
|
|
|
|
|
|
|
|
|
Поскольку E = |
0 0 |
, а максимальная скорость v |
|
= w |
x |
|
, то пло- |
|||
|
0 |
0 |
||||||||
|
2 |
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
щадь внутри фазовой кривой, является адиабатическим инвариантом
x0v0 = const . |
(59.8) |
Формула (59.7) справедлива для случая, когда масса не меняется. Изменение массы означает, что система незамкнута, и для решения задачи нужно учитывать механизм изменения массы (может испаряться, могут прилипать ранее покоившиеся частицы). В случае испарения тело теряет массу без внешнего воздействия, тогда вместо (59.5) получится
|
|
|
2 |
|
|
2xx |
|
|
2mxx |
+m x |
2 |
|
2 |
+m x |
2 |
|
|
|||||
E |
= |
kx |
|
+k |
|
+ |
|
= |
kx |
|
+x (kx +mx) |
= |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
2 |
2 |
|
(59.9) |
||||
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|||||||||||
|
|
|
|
x |
2 |
æ |
|
m |
ö |
|
E |
|
|
|
|
|
|
|
|
|||
|
kx |
+m |
|
çk |
|
÷ |
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
|
= ç |
|
+ |
|
÷ |
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
m |
÷ |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
èk |
|
ø |
|
|
|
|
|
|
|
|
|
|||||||
153

Отсюда
dE |
= |
1 dk |
+ |
1 dm |
ln E = |
1 lnkm +const |
|
E |
= const. |
||
|
|
|
|
||||||||
E |
|
2 k |
|
2 m |
|
2 |
|
|
|
km |
|
|
|
|
|
|
I = |
E |
. |
(59.10) |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
km |
|
|
|
|
Примеры.
1) Математический маятник (маленькое тело на нитке в поле тяжести)
В этом случае уравнение колебаний mx = -mgx/l , т.е. эффективный
коэффициент жесткости |
k* = mg/l. Тогда I = E |
l |
. При испарении |
|
g |
||||
|
m |
|
E µ m , что естественно, т.к. при испарении доля уносимой энергии пропорциональна отделившейся массы. Более удивительным является
возрастание энергии колебаний при укорочении нитки: E µ 1/ l. Это
связано с тем, что при втягивании нитки через точку подвеса совершается работа не только против силы тяжести (mg ), но и против допол-
нительного натяжения нити, связанного с колебаниями (mv2/l ). Именно эта дополнительная работа дает увеличение энергии.
2)Тело на пружинке.
Вэтом случае инвариант дается уравнением (59.10). При медленном
испарении E µ m . Заметим, что при испарении только в точке с максимальной амплитудой энергия не зависела бы от массы, а при испарении только в точке с максимальной скоростью энергия была бы пропорциональна массе. При адиабатическом испарении получается промежуточный результат.
Интересно, что при увеличении коэффициента жесткости энергия колебаний увеличивается. Откуда она берется? Что значит увеличить жесткость в момент, когда пружинка уже частично растянута? Для этого к ней нужно прицепить параллельно еще одну растянутую пружинку. Вот она и приносит дополнительную энергию.
154

Г Л А В А VII
ВОЛНЫ В УПРУГОЙ СРЕДЕ
§ 60. Упругие среды
Деформации тел под действием сил называются упругими, если при снятии напряжения их размеры восстанавливаются. При небольших относительных деформациях относительное удлинение пропорционально приложенной силе, деленной на поперечное сечение
|
T = -P = F |
= E Dl |
º Ee º kDl |
, |
(60.1) |
||||||||||
|
|
|
|
|
S |
|
|
|
l |
|
|
S |
|
|
|
F |
|
|
F |
где E |
– модуль Юнга, |
Dl |
, |
||||||||
|
|
||||||||||||||
|
|
|
|
|
e = l |
||||||||||
|
|
|
Z |
|
|
|
|
F |
|
|
ES |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l . Данное соотношение на- |
||||
|
Рис. 43 |
|
|
|
k |
º Dl = |
|
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
зывается законом Гука. |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
При продольном растяжении (вдоль Z) поперечные размеры стерж- |
|||||||||||||||
ня уменьшаются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
= Dy |
= -m Dz |
º -m Dl , |
|
(60.2), |
|||||||
|
|
|
x |
|
y |
|
|
|
|
z |
|
|
l |
|
|
где m– коэффициент Пуассона. |
|
|
|
|
|
|
|
||||||||
Изменение объема при растяжении в одном направлении |
|
||||||||||||||
|
DV |
|
Dx |
|
Dy |
Dz |
|
Dz |
(1 -2m), |
(60.3) |
|||||
|
V |
|
= |
x |
+ |
|
y + |
|
z |
|
= z |
||||
так, что при m = 1 |
объем сохраняется. Для резины m » 0.5 , металлов |
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m » 0.3 , алмаза 0.07. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
При равномерном обжатии |
|
|
|
|
|
|
|
||||||||
|
|
|
e |
= e = e = -P |
(1 -2m), |
|
(60.4) |
||||||||
|
|
|
x |
|
y |
|
z |
|
E |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отсюда
155
|
DV = Dx + Dy + Dz = e |
+ e |
+ e = - P |
, |
(60.5) |
||||
|
V |
x y z |
x |
y |
z |
K |
|
|
|
|
|
|
|
|
|
||||
гдеK = |
E |
– коэффициент объемного сжатия. |
|
|
|
||||
|
|
|
|
|
|||||
3(1 -2m) |
|
|
|
||||||
Коэффициент Пуассона не может быть больше 0.5, иначе при прикладывании внешнего давления объем будет расти, и тело будет совершать работу. При снятии давления объем вернется к прежнему значению. Процесс можно повторить много раз, получается неисчерпаемый источник энергии, что невозможно.
Рассмотрим стержень, который не может расширяться вбок, т.к. с боков очень твердая среда. Тогда при приложении Pz возникают
Px ,Py , такие, что поперечные размеры не меняются
|
|
|
e |
|
= Dx |
= - |
Px |
+ |
|
m |
|
(P |
+P ) = 0 |
|
|
||||||||||||||
|
|
|
|
E |
E |
|
|
|
|||||||||||||||||||||
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
z |
|
|
|
|
|||||
|
|
|
e |
= |
Dy |
= - |
Py |
+ |
|
|
m |
|
(P |
+ P ) = 0. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
y |
|
|
y |
|
|
|
|
E |
|
|
E |
|
|
x |
|
|
|
z |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= P |
|
= |
|
|
m |
|
|
P , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 - m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
y |
|
|
z |
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
ö |
|
|
|||||||
|
|
P |
|
|
|
(Px + Py ) |
|
|
|
|
P |
|
|
|
2m |
2 |
P |
|
|||||||||||
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
÷ |
z |
|
|
ez |
= - |
|
|
|
+ m |
|
|
|
|
|
|
= - |
|
|
ç |
|
|
|
|
|
÷ = - |
|
, |
||||||
E |
|
|
|
E |
|
|
|
|
|
ç1 - |
|
|
|
|
E ¢ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E ç |
|
1 - m÷ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
1 - m |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
E |
= E (1 + m)(1 -2m) |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(60.6)
(60.7)
(60.8)
– модуль одностороннего сжатия. Например, если резинку поместить в металлическую трубку, то в продольном направлении у нее будет очень малая сжимаемость и, соответственно, очень большой эффективный модуль Юнга.
156

§ 61. Волны в среде, модель с шариками
Представим среду как линейку из стоящих вплотную шариков. Если крайнему шарику сообщить скорость, то он ударится о следующий шарик и остановится, передав ему весь свой импульс. Далее второй шарик ударит по третьему шарику, и остановится, и.т.д. В каждый момент в движении будет находиться только один шарик, а конце будет двигаться только последний шарик.
Если после того как первый шарик остановится, по нему снова ударить, то по цепочке побежит волна, состоящая из двух шариков. В конце, все шарики будут стоять, кроме двух последних.
Теперь заменим шарики тонкими пластинками, стоящими вплотную друг к другу (получается стержень), и начнем ударять по первой пластинке после каждой ее остановки. По стопке побежит волна длительностью равной времени воздействия на торец стержня. При устремлении толщины пластинки к нулю удары становятся бесконечно частыми, и воздействие сводится к действию постоянной силы.
§ 62. Скорость звука в упругой среде
|
A |
B |
Приложим силу F к концу стержня, |
||||||||
F |
тогда он начнет двигаться с некоторой |
||||||||||
v |
|
c |
|
||||||||
|
скоростью v . Пусть v c , тогда |
||||||||||
|
|
||||||||||
|
|
||||||||||
|
|
Рис. 44 |
d(mv) |
= F, |
(62.1) |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
dt |
|
|
|||
|
|
|
|
|
mv » (r + dr)S(c -v)vt » rScvt. |
|
|||||
|
|
Отсюда |
|
P = F/S = rcv . |
(62.2) |
||||||
Относительное сжатие части стержня АВ равно |
|
||||||||||
|
|
|
Dl |
= -vt |
= -v |
(62.3) |
|||||
|
|
|
l |
|
ct |
|
|
t |
|
||
(левый край передвинулся на vt ). Отсюда |
|
||||||||||
|
|
|
P = -E Dl |
= E v . |
(62.4) |
||||||
|
|
|
|
|
|
l |
|
|
c |
|
|
Приравнивая (62.2) и (62.4), получаем скорость звука для среды, подчиняющейся закону Гука,
157
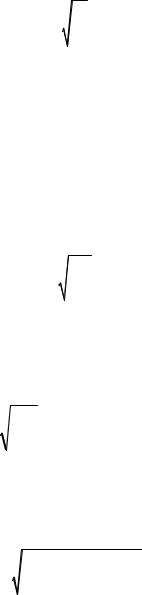
c = |
E . |
(62.5) |
|
r |
|
В общем случае, вместо (62.4) можно записать уравнение непрерывности на движущейся границе B. Переходим в систему отсчета движущегося фронта B, спереди фронта за единицу времени падает масса rc , а
за фронт уходит (c -v)(r +dr). Из сохранения потока
rc = (c -v)(r +dr), dr » r v |
(62.6) |
c |
|
(этот результат похож на (62.3), т.к. dr/r = -dl/l ). Объединяя (62.2) и (62.6), находим скорость звука
c = |
dP . |
(62.7) |
|
dr |
|
В случае закона Гука, dr = -rldl = rdPE и для скорости звука по-
лучаем формулу (62.5). В курсе молекулярной физике, используя (62.7), будет получена скорость звука в газе
c = g |
P |
, |
где g = |
cP |
. |
(62.8) |
r |
|
|||||
|
|
|
c |
|
||
|
|
|
|
V |
|
|
Следует заметить, что формула (62.5) справедлива только для тонких стержней, когда ничего не мешает стержню расширяться вбок. В
противном случае вместо E нужно использовать E ¢ |
(ф-ла (60.8)), то- |
|||||
гда продольная скорость |
|
|
|
|
|
|
c = |
E |
1 - m |
|
. |
(62.9) |
|
r (1 + m)(1 -2m) |
||||||
|
|
|
||||
|
|
|
|
|
||
Эта скорость больше, чем в тонком стержне. Приближением толстого стержня работает в случаях: 1) стержень находится в очень жесткой трубке, 2) длина стержня короче толщины, 3) длина волны меньше толщины стержня.
Для справки: существуют еще и поперечные волны (частицы колеблются поперек движения волны). Для них
158
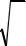
|
c |
^ |
= |
|
G , |
|
(62.10) |
|
|
|
|
|
r |
|
|
||
|
|
|
|
|
|
|
||
где модуль сдвига G = |
E |
|
|
, при этом всегда |
c > c > c . |
|||
2(1 + m) |
||||||||
|
|
|
^ |
|||||
|
|
|
|
|
|
|||
Поперечные волны существуют только в твердом веществе, в жидкости при сдвиге слоев не возникает возвращающих сил. Именно по этому признаку геологи различают твердые и жидкие породы.
§ 63. Волновое уравнение
Рассмотрим звуковую волну в газе. При распространении волны происходит 3 явления
1.Газ движется, плотность меняется.
2.При изменении плотности меняется давление.
3.Неравномерность давления вызывает движение газа.
Начнем с пункта 2. В общем случае P = f(r). В равновесии P0 = f (r0 ). Отсюда отличие давления и плотности от равновесных значений в звуковой волне
P = kr , где k = |
¶P |
. |
(63.1) |
|
|
||||
u |
u |
¶r |
|
|
|
|
|
||
Здесь индекс u относится к изменению давления и плотности в волне. Теперь используем явление 1. Пусть в волне продольное (X) смещение частиц y(x,t), и в данный момент времени это смещение различно для
точек с разными начальными координатами x . Тогда возникает изменение плотности. Пусть x невозмущенное положение частицы. В волне она сместится в точку x + y(x,t). Другая невозмущенная частица с ко-
ординатой x + Dx при этом сместится в точку x + Dx + y(x + Dx,t). Частицы, которые находились в интервале Dx , теперь будут нахо-
диться в интервале |
Dx + y(x + Dx,t) -y(x,t) = Dx + |
¶y Dx , где |
|
|
¶x |
второй член много меньше первого, т.к. смещения малы. Из сохране-
|
æ |
ö |
ния числа частиц r0Dx = (r0 |
ç |
¶y÷ |
+ ru )Dx ç1 + |
÷. |
|
|
ç |
÷ |
|
è |
¶x ø |
159
Отсюда r |
+ r » r |
|
Dx |
|
|
|
» r |
|
|
- r |
|
¶y и |
||
|
æ |
|
ö |
|
|
|
||||||||
0 |
u |
0 |
|
|
|
0 |
|
|
0 |
¶x |
||||
ç |
¶y÷ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Dx 1 + |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
||
|
|
|
è |
¶x ø |
|
|
|
|
|
|
|
|
||
|
|
|
r |
» -r |
|
|
¶y |
. |
|
(63.2) |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
u |
|
|
|
0 |
|
¶x |
|
|
||
Наконец, явление 3 дает уравнение движения объема частиц в интервале Dx
æ |
¶ |
2 |
y |
ö |
|
|
¶Pu |
|
|
|
|
|
|
|
|
æ |
2 |
|
|
ö |
|
|
|
¶Pu |
|
|
|||||
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
ç |
¶ |
y÷ |
|
|
|
|
|
|||||||||||
ç |
|
|
|
2 |
|
÷ |
= - |
|
|
|
|
Dx |
|
|
|
r0 |
ç |
|
|
2 |
÷ |
= - |
|
|
. |
(63.3) |
|||||
r0Dx ç |
|
|
|
|
÷ |
|
dx |
|
|
|
ç |
|
|
÷ |
|
dx |
|||||||||||||||
ç |
¶t |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
ç |
¶t |
|
÷ |
|
|
|
|
|
|
||||||
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
2 |
|
|
ö |
|
|
|
|
|
¶ru |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
¶ |
y÷ |
|
|
|
|
|
|
|
|
|
|||||
Подставляя (63.1) в |
(63.3) |
имеем |
r0 |
ç |
|
|
|
2 |
÷ |
= -k |
|
|
|
, и, |
учитывая |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
÷ |
|
dx |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
¶t |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|||
(63.2), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
2 |
|
|
ö |
|
|
2 |
2 |
y |
|
|
2 |
|
|
|
|
|
|
|
¶P |
|
|
|
|
|
|||
|
ç |
¶ |
y÷ |
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
2 |
= c |
|
|
|
2 , |
|
c |
|
= k = |
|
|
|
. |
|
|
|
(63.4) |
||||||||
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ç |
¶t |
|
÷ |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
¶r |
|
|
|
|
|
||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Нетрудно убедиться, что решением волнового уравнения являются функции
æ |
ö |
|
ç |
x ÷ |
(63.5) |
y(x,t) = yçt |
÷, |
|
ç |
÷ |
|
è |
c ø |
|
т.е. любые функции, описывающие возмущения в среде, бегущие влево и вправо со скоростями c . Действительно, подставляя (63.5) в (63.4),
получаем в левой части y¢¢ и в правой y¢¢, где производная y¢¢берется по аргументу функции (t x / c), т.е. решение (63.5) удовлетворяет
волновому уравнению (63.4). Это бегущая волна, поскольку, если в точке x = 0 в момент t = 0 было возмущение y(0), то такое же воз-
мущение будет через время t в точке x = ct . Таким образом, общее решение волнового уравнения
|
æ |
ö |
|
æ |
ö |
|
y(x,t) = y |
ç |
x ÷ |
+ y |
ç |
x ÷ |
(63.6) |
çt + |
÷ |
çt - |
÷. |
|||
1 |
ç |
÷ |
2 |
ç |
÷ |
|
|
è |
c ø |
|
è |
c ø |
|
Заметим, что скорость звука (63.4) совпадает с полученным ранее выражением (62.7).
160
