
telnov-machanika-and-TO
.pdf
уравнения, заданыp1, p2,q , нужно найти p1¢, p2¢ и угол второй частицы.
Можно в лоб, путем подстановок, решить эту систему из трех уравнений. Однако мы сделаем это проще, воспользовавшись операциями с векторами. Данная техника нам понадобится для решения подобной задачи в релятивистском случае.
Возьмем из (37.1) p2¢ = p1 + p2 -p1¢и подставим в (37.2). В результате остается одно уравнение
|
|
|
|
|
|
|
|
|
|
|
p12 |
|
|
+ |
|
|
p22 |
|
|
= |
|
p1¢2 |
|
|
|
+ |
|
(p1 + p2 -p1¢)2 |
, |
|
|
|
|
|
|
|
|
|
(37.3) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2m |
|
2m |
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
неизвестным |
является |
p1¢. Раскрывая и |
сокращая |
|
одинаковые |
||||||||||||||||||||||||||||||||||||||||||||||||||
члены, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
p12 |
|
= |
|
p1¢2 |
|
+ |
|
|
p12 |
|
|
+ |
|
p1¢2 |
|
|
|
+ |
|
2p1p2 |
- |
2p1p1¢ |
- |
|
2p2p1¢ |
. |
|
|
|
|
(37.4) |
|||||||||||||||||||||
|
|
|
|
2m |
|
2m |
|
|
2m |
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2m |
2 |
|
|
|
|
2m |
2 |
|
|
|
|
|
2m |
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
p1p2 |
= -p1p2 , p1p1¢ = p1p1¢cos q, p2p1¢ = -p2p1¢cos q, |
|
|
|
|
(37.5) |
|||||||||||||||||||||||||||||||||||||||||||||||
получаем квадратное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
p1¢2 -2p1¢ |
(p - p )m cos q |
- |
|
|
|
2p p m |
|
- |
p2 |
(m |
2 |
-m ) |
= |
0 |
, (37.6) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
1 2 1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
m1 +m2 |
|
|
|
|
|
m1 +m2 |
|
|
m1 +m2 |
|
|||||||||||||||||||||||||||||||||||||||||
откуда находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
p1¢ = |
(p - p )m cos q |
|
(p - p )2 m2 cos2 q |
|
|
|
|
2p p m |
|
|
|
+ |
p2(m -m ) |
(37.7) |
||||||||||||||||||||||||||||||||||||||||||
1 |
m +m |
|
|
|
|
|
1 |
(m +m )2 |
|
|
|
+ m +m |
|
|
|
m +m |
|
1 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|||||
Происхождение двойного решения такое же, как и при распаде частиц. В случае покоящейся второй частицы, p2 = 0 , формула упрощается
|
|
æ |
|
m1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
ö |
|
|
|
ç |
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
÷ |
|||
p¢ = p |
ç |
|
|
|
cos q |
|
|
|
|
|
|
m |
2 |
-m |
sin |
q÷. |
||
|
|
|
|
|
|
|
|
|
||||||||||
1 |
1 |
ç |
|
+m |
|
|
m |
+m |
|
|
1 |
|
|
÷ |
||||
|
|
çm |
2 |
|
2 |
|
|
|
|
|
÷ |
|||||||
|
|
è 1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
ø |
|||
При m1 > m2 |
перед корнем допустимы оба знака, при m2 |
> m1 |
||||||||||||||||
+. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При m1 > m2 |
максимальный угол рассеяния |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
sin q |
|
= |
m2 |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
макс |
|
|
m1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(37.8)
– знак
(37.9)
При q = 0 и m1 > m2 имеем
91
p1¢ = p1 или p1¢ = |
m1 |
-m2 |
p1 , |
p2¢ = p1 - p1¢ = |
2m1m2 |
|
v1. (37.10) |
||
m |
+m |
2 |
m |
+m |
2 |
||||
1 |
|
|
1 |
|
|
||||
Первое решение – это пролет мимо (легкое касание), второе – лобовое столкновение, причем при равных массах налетающая частица останавливается.
В случае лобового столкновения m1 < m2 налетающая частица полетит назад ( q = p ), при этом
p1¢ = |
m -m |
p1 . |
(37.11) |
|
2 |
1 |
|||
m |
+m |
|||
1 |
2 |
|
|
|
Из (37.10) следует, что при столкновении бесконечно тяжелой стенки с покоящейся частицей последняя приобретает скорость
v2¢ = 2v1 . Этот результат можно легко получить, перейдя в систему стенки, где покоящаяся частица налетает на стенку со скоростью v1 и
отскакивает с той же скоростью. Переходя обратно в лабораторную систему, получаем v2¢ = v1 +v1 = 2v1 .
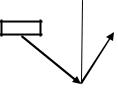
Столкновение в случае трения
|
Пусть брусок налетает под углом q1 |
q2 |
на бесконечно тяжелую плоскость, ко- |
эффициент трения с которой k . Найдем |
|
q1 |
угол отражения, считая соударение упру- |
гим.
|
Здесь, хотя и все деформации упру- |
|
Рис. 28 |
гие, т.е. в самих телах тепло не выделя- |
|
ется, однако энергия может теряться за |
||
|
счет силы сухого трения. Сила трения может уменьшить горизонтальный импульс. Вертикальный же импульс при ударе сохраняется по величине, но меняет направление, отсюда
F^t = 2p cos q1 . |
(37.12) |
При проскальзывании сила трения равна kF^ , тогда конечный продольный импульс
p¢ = p sin q1 -kF^t = p sin q1 -2kp cos q1 . |
(37.13) |
Отсюда находим угол отскока
92

tg q |
= |
p¢ |
= |
sin q1 -2k cos q1 |
= tg q -2k . |
(37.14) |
|
|
|
||||||
2 |
p^ |
|
cos q |
1 |
|
||
|
|
|
1 |
|
|
||
При получении этой формулы мы предположили, что имеет место проскальзывание в течение всего времени взаимодействия. Но проскальзывание прекращается, когда горизонтальная скорость становится равной нулю, отсюда следует, что
tg q2 = 0 при tg q1 < 2k . |
(37.15) |
Есть еще один режим, когда проскальзывания нет вообще. При этом сила будет действовать против полной скорости, что приведет к полной остановке тела, а затем силы деформации отбросят тело точно назад. Поскольку сила действует в направлении скорости, то условие
непроскальзывания, «заклинивания», F < kF^ , т.е. F sin q1 < Fk cos q
|
|
|
|
или tg q1 < k . Именно при этих углах тро- |
|||
tg q2 |
|
|
сточка не будет проскальзывать, с какой |
||||
|
|
|
|
бы силой на нее ни давили. |
|
||
|
|
|
|
tg q2 |
= -tg q1 при |
tg q1 < k . |
(37.16) |
k |
|
tg q1 |
В итого имеем: |
|
|
||
|
|
|
|
tg q2 = tg q1 -2k tg q1 > 2k ; |
|
||
|
|
2k |
|
||||
|
|
|
Рис. 29 |
tg q2 |
= 0 |
k < tg q1 |
< 2k |
|
|
|
|
tg q2 |
= -tg q1 |
tg q1 < k |
(37.17) |
§ 38. Закон сохранения момента импульса
До сих пор мы упоминали момент импульса только в связи с третьим законом Ньютона, не вдаваясь в детали. Третий закон Ньютона гла-
сит: силы взаимодействия двух материальных точек i и k равны по модулю и действуют вдоль прямой, соединяющей эти материальные
точки: Fik = -Fki . Этот постулат означает, что в любой замкнутой
системе сохраняется момент импульса. Выясним, что это такое. По определению, момент импульса системы частиц это
L = å[ri × pi ]. |
(38.1) |
Для одной частицы L = r^p = rp^ , где r^ = r sin q , p^ = p sin q , т.е момент импульса материальной точки (частицы) относительно точки
93
начала отсчета равен импульсу тела, умноженному на длину перпендикуляра, опущенного из начала отсчета на траекторию частицы. Момент импульса направлен перпендикулярно плоскости, лежащей на векторах r и p . Это аналогично движению точки по окружности, рас-
смотренному ранее, где был введен вектор угловой скорости, направленный перпендикулярно плоскости движения, вдоль оси вращения.
Все взаимодействия в системе частиц можно рассматривать как сумму взаимодействий пар частиц. Для любой пары
dL = r |
× p |
+ r × p |
1 |
+ r |
× p |
+ r × p |
2 |
. |
(38.2) |
|
dt |
1 |
1 |
1 |
2 |
2 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что p1 = -p2 , получаем
dL = r |
× p |
+ r |
× p |
2 |
+(r |
- r )× p |
2 |
= 0 . |
(38.3) |
|
dt |
1 |
1 |
2 |
|
2 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Здесь первые два члена равны нулю потому, что скорость и импульс частицы имеют одинаковое направление и их векторное произведение равно нулю. Третий член равен нулю вследствие третьего закона Ньютона (поскольку сила параллельна радиус-вектору, соединяющему частицы). Таким образом, в природе имеет место закон сохранения мо-
мента импульса.
Следствия этого закона рассматриваются в разделах движение твердого тела и движение в центральном поле.
§ 39. О происхождении законов сохранения энергии, импульса и момента импульса
Закон сохранение энергии
Энергии для системы частиц
E = K +U |
= å |
miv2i |
|
+U(r1,r2....rn ,t) , |
(39.1) |
||||||||||
2 |
|||||||||||||||
ее изменение во времени |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dE |
|
dvi |
|
dUi dri |
|
¶U |
|
||||||||
dt = åmi vi |
|
|
|
+ å |
|
|
|
|
+ |
¶t dt |
(39.2) |
||||
dt |
dr |
|
dt |
|
|||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
= åvi (mi |
|
dvi |
-Fi ) + |
¶U |
= |
0 + |
¶U . |
(39.3) |
|||||||
|
|
¶t |
|||||||||||||
|
|
dt |
|
|
|
|
|
|
¶t |
|
|||||
Выражение в скобке равно нулю по второму закону Ньютона. Таким образом: закон сохранения энергии работает, если потенциальная
94
энергия явным образом не зависит от времени, а является функцией только координат.
Закон сохранения механической энергии связан с однородностью времени, что означает, что физические законы не зависят явным образом от времени.
Пример несохранения энергии: пусть мяч подбросили вверх с некоторой скоростью и, пока он летит, вверх ускорение свободного паде-
ния равно g1 , а когда падает вниз, то g2 . В этом случае мяч вернется на
землю с другой скоростью, т.е. полная энергия не сохраняется. Для того, чтобы поменялась g при неизменной массе и размерах Земли нуж-
но, чтобы изменилась фундаментальная константа G .
Закон сохранения импульса
Пусть имеется система частиц, в которой на i -ю частицу действуют сила Fi со стороны остальных частиц. Прикладывая бесконечно малые
внешние силы, сместим всю систему на dR , не изменяя взаимного расположения частиц в системе. Суммарная работа всех сил равна нулю, поскольку пространство однородно и внутренняя энергия системы не зависит от места системы в пространстве, т.е.
dA = dRåFi = 0 . |
(39.4) |
i |
|
Отсюда получаем, что åFi – сумма сил в системе равна нулю, а,
i
следовательно, суммарный импульс системы сохраняется. Таким обра-
зом, закон сохранения импульса обусловлен однородностью пространства.
Например, если бы в пространстве были невидимые нам тела, действующие неизвестными нам силами на наблюдаемые тела, то мы заключили бы, что импульс не сохраняется.
Закон сохранения момента импульса.
Используем ту же логику, что и при рассмотрении закона сохранения импульса, но не для сдвига, а для поворота системы в пространстве. Пусть имеется система частиц, в которой на i -тую частицу дейст-
вуют силы Fi со стороны остальных частиц. Прикладывая бесконечно малые силы, повернем всю систему на угол φ, не меняя взаимного
расположения частиц в системе. Суммарная работа всех сил равна нулю, поскольку пространство изотропно и внутренняя энергия системы не зависит от ориентации системы в пространстве:
95
dA = åFidri = åFi[dφ´ri ] = dφå[ri ´Fi ] = dφå[ri ´pi ] = 0 (39.5)
i |
i |
i |
i |
Величина éêëri ´Fi ùúû = éêëri ´pi ùúû – это момент сил, действующий на части-
цу. Это означает, что сумма моментов сил в изолированной системе равна нулю. Отсюда,
dL |
= å(ri × pi + ri × pi ) = 0 |
(39.6) |
dt |
|
|
Здесь первая сумма равна нулю вследствие параллельности скорости и импульса, а вторая сумма равна нулю из-за равенства нулю момента сил.
96
Г Л А В А V
РЕЛЯТИВИСТСКАЯ ДИНАМИКА.
§ 40. Релятивистский импульс
Ясно, что в релятивистском случае закон сохранения импульса в виде
m1v1 +m2v2 = const |
(40.1) |
несправедлив, т.к. не содержит ограничения на максимальную скорость частиц. В нерелятивистском случае мы просто постулировали закон сохранения импульса при рассеянии частиц, взяв выражение для импульса в виде p = mv (при другом подходе закон сохранения
импульса следует из уравнений Ньютона, которые также являются постулатами). Будет ли вообще аналог закона сохранения импульса в релятивистском случае, если не вводить дополнительных постулатов?
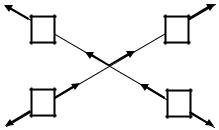
Рассмотрим такую конструкцию. Два тела с большими массами 1 и 2 выстреливают по легкому релятивистскому ядру, которые, рассеявшись друг на друге, застревают в массивных поглотителях 3 и 4, см.
рис. 30.
Если наблюдать только за большими телами, которые имеют нерелятивистские скорости, то для них можно записать равенство нулю суммарного импульса
|
|
|
|
|
(-p1) +(-p2 ) + p1¢ + p2¢ = 0 |
(40.2) |
||||
или |
|
|
|
|
p1 + p2 |
= p1¢ + p2¢ . |
(40.3) |
|||
Отсюда следует существование закона сохранения импульса для |
||||||||||
релятивистских частиц. В рассуждениях мы сделали только одно |
||||||||||
естественное предположение, что при выстреле покоящимся телом |
||||||||||
ядра импульс отдачи равен импульсу ядра. |
|
|
|
|||||||
|
|
|
|
|
|
|
Теперь осталось найти выра- |
|||
|
|
|
|
|
|
p2 |
жение |
для релятивистского им- |
||
p1 |
|
|
|
|
|
пульса, при котором закон сохра- |
||||
|
3 |
|
|
|
4 |
|
||||
|
|
|
|
|
нения |
импульса, |
записанный |
в |
||
|
|
|
|
|
|
|
|
|
||
|
|
p1 |
p2 |
|
|
одной из систем отсчёта, будет |
||||
|
|
|
|
|
|
|
||||
|
|
p1 |
|
|
p |
|
автоматически выполняться при |
|||
|
|
|
|
|
переходе в любую другую инер- |
|||||
p1 |
1 |
|
|
|
2 |
p2 |
||||
|
|
|
2 |
циальную систему отсчёта. Мы |
||||||
|
|
|
|
|
|
|
рассмотрим два подхода к этой |
|||
|
|
Рис. 30 |
|
|
|
задаче. |
|
|
|
|
|
|
|
|
|
|
|
97 |
|
|
|

Первый способ основан на поиске выражения для релятивистского импульса путем рассмотрения частных случаев взаимодействия частиц и требования инвариантности явления при переходе в другую систему отсчёта. Второй способ, более формальный, опирается на свойства 4-
векторов. |
|
|
|
|
|
|
|||
Будем искать выражение для импульса в виде |
|
|
|
||||||
|
|
|
|
p = f (v)mv , |
|
|
(40.4) |
||
|
|
|
|
|
где f (v) |
– некоторая функция |
|||
Y |
|
скорости, |
стремящаяся |
к |
|||||
|
|
|
|
|
единице при v 0 . Рассмотрим |
||||
|
|
|
|
|
два поезда, |
движущиеся |
с |
||
|
|
|
равными |
скоростями |
навстречу |
||||
|
|
2 |
|
||||||
|
|
|
|
|
друг другу (рис. 31). С поездов |
||||
|
|
|
|
|
навстречу |
друг |
другу |
стреляют |
|
|
1 |
|
|
X |
ядрами, |
так |
что |
в |
|
|
|
|
|
||||||
|
|
|
|
сопутствующих |
|
поездам |
|||
|
|
|
|
|
|
||||
|
Рис. 31 |
|
системах |
отсчёта |
скорость |
||||
|
|
|
|
|
выпущенных |
|
ядер |
||
перпендикулярна направлению движения и равна vy , причем vy c .
Ядра встречаются и слипаются. Из симметрии ясно, что в неподвижной системе импульс образованного тела равен нулю. Тогда, в системе поезда 1 это тело не движется в поперечном направлении и его поперечный импульс равен нулю. Отсюда суммарный поперечный импульс ядер до столкновения также равен нулю, т.е.
|
mvy = m f (v¢)vy¢ . |
(40.5) |
Здесь |
в левой части написан нерелятивисткий импульс, поскольку |
|
ранее |
предположили, что vy c . Здесь vy¢ и v¢ |
– соответственно |
вертикальная и полная скорость ядра, выпущенного с поезда 2, в системе поезда 1. Пусть относительная скорость поездов равна V , тогда из формул преобразования для Y -скоростей (22.4) с учетом,
чтоvx ядра в системе своего поезда 2 равна нулю, находим
vy¢ = vy |
1 -V |
2 |
c2 . |
(40.6) |
||
Из (40.6) и (40.5) следует |
|
|
|
|
|
|
¢ |
-V |
2 |
c |
2 |
= 1. |
(40.7) |
f (v ) 1 |
|
|
||||
Устремим vy к нулю, тогда v¢ V , следовательно,
98
f (V ) = |
1 |
. |
(40.8) |
|
1-V 2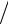 c2
c2
Врезультате получаем искомое выражение для импульса при произвольных скоростях
|
p(v) = f (v)mv = |
|
|
mv |
. |
(40.9) |
|||||||
|
|
1 -v2 c2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
При этом закон сохранение импульса будет имеет вид |
|
||||||||||||
|
åpi º å |
|
|
mi vi |
|
|
|
= const |
(40.10) |
||||
|
|
|
1 -v2 |
c2 |
|||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
Заметим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p = m u |
= |
|
m v |
|
. |
|
(40.11) |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 -v2/ c2 |
|
|
||||||
где |
u = dr = |
|
|
v |
|
|
|
- 4-скорость |
(40.12) |
||||
|
|
|
|
|
|
|
|||||||
|
dt |
|
1 - v |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
c2 |
|
|
|
|
||||
Это выражение совпадает с формулой (40.9), полученной на частном примере. Закон сохранения импульса будет выглядеть как
åpi |
= åpj , где p = mu = |
mv |
. |
(40.13) |
|
1 -v2 / c2 |
|||||
i |
j |
|
|
§ 41. Релятивистская энергия
Рассмотрим распад тела с массой M на две части с массами m1 и m2 . В системе покоя исходного тела разлет происходит в противопо-
|
|
|
|
|
ложных направлениях, рис. 32. По- |
||||
|
v1 |
|
v2 |
|
смотрим теперь |
этот |
же |
процесс |
|
m1 |
M |
m2 |
распада в системе отсчёта, |
имеющей |
|||||
|
|
|
|
|
поперечную |
к |
v1 и |
v2 |
скорость |
|
|
|
|
|
|||||
|
|
v =0 |
|
|
w c , рис. |
33. Закон |
сохранения |
||
|
|
|
|
|
|||||
|
|
Рис. 32 |
|
|
для вертикальной компоненты им- |
||||
|
|
|
|
пульса имеет вид |
|
|
|||
99
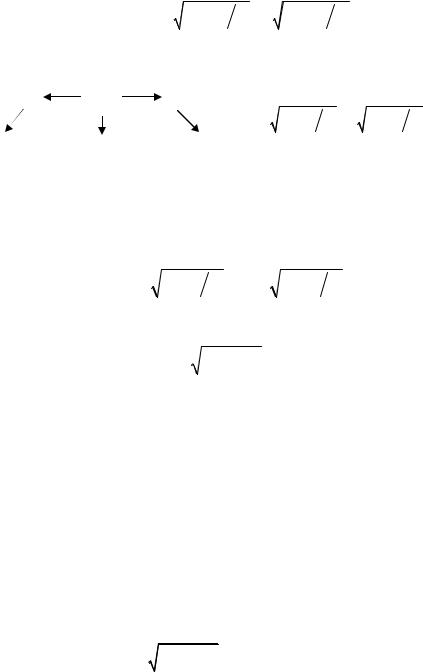
|
|
|
|
Mw = |
|
|
|
m1w |
|
|
+ |
|
|
m2w |
|
|
(41.1) |
|||||
|
|
|
|
|
|
1 -v1¢2 c2 |
|
|
1 -v2¢2 c2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Устремим w к нулю, тогда v1¢ v1 и |
|
v2¢ v2 . Сократив обе части на |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
w , получаем |
|
|
|
|
|
|
|
|||||
|
m |
|
M |
|
|
m |
|
|
M |
= |
|
|
m1 |
|
+ |
|
m2 |
|
(41.2) |
|||
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 -v2 |
c2 |
1 -v2 |
c2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
v1¢ |
|
|
|
|
|
|
|
v2¢ |
|
|
|
1 |
|
|
|
|
2 |
|
|
|||
|
w |
|
|
|
т.е. исходная масса не равна сумме |
|||||||||||||||||
|
|
|
Рис. 33 |
|
|
|
|
конечных масс и |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
M > m1 +m2 |
. |
(41.3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Поскольку исходная масса могла бы распасться и на другие состав-
ляющие, то (41.2) можно переписать в виде |
|
|
|
|
||||||||||
å |
|
|
m c2 |
|
|
= å |
|
m c2 |
|
|
|
|
||
|
|
i |
|
|
|
j |
|
|
. |
(41.4) |
||||
|
1 |
2 |
c |
2 |
2 |
c |
2 |
|||||||
i |
-vi |
|
j |
|
1 -vj |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Введем обозначение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = |
|
mc2 |
= gmc2 |
|
|
|
(41.5) |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
1-v2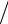 c2
c2
иназовем эту величину релятивистской энергией частицы. К такому термину есть основания: при v 0
E = mc2 + |
mv2 |
, |
(41.6) |
|
|||
2 |
|
|
|
т.е. энергия отличается от энергии в покое на нерелятивистскую кинетическую энергию.
В этих терминах (41.4) можно записать в виде
åEi = åEj , |
(41.7) |
– это закон сохранения энергии в релятивистском случае. При малых скоростях он переходит в нерелятивистский закон сохранения кинетической энергии. Кинетической энергией в общем случае можно назвать величину
T = |
mc2 |
-mc2 = (g -1)mc2 . |
(41.8) |
|
1 -v2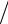 c2
c2
100
