Физ химия и физ т.д

Х и м и ч е с к а я к и н е т и к а

статистического веса данного энергетического состояния молекулы gi , то в

случае непрерывно изменяющейся энергии его можно получить, применяя принцип неопределенности Гейзенберга. Из этого принципа следует, что наименьшее определимое значение произведения приращений координаты dq и

сопряженного с ней импульса dp определяется условием

где = = 2hπ =1,055 10−34 Дж с – постоянная, иногда называемая постоянной

Планка – Дирака [13]; h = 6,626 10−34 Дж с – постоянная Планка. В квантовой статистике объем элементарной ячейки фазового пространства1 принимается

равным (2π=)f = h f , где f – число степеней свободы движения.

Кратко рассмотрим одномерное движение. Пусть энергия поступательного движения частицы массой m вдоль координаты x составляет εi = mx2 / 2 (m –

масса, x = dx / dτ – скорость), а «объем» элементарной ячейки равен h (f = 1, так как движение одномерное). Отсюда статистический вес рассматриваемого энергетического состояния молекулы с координатами между x и x + dx и скоростями между x и x + dx будет

Следовательно, доля молекул, обладающих такими характеристиками, выразится

Интегрируя2 (2.260) по x от −∞ до + ∞ и по x от 0 до a, где a – длина отрезка,

на котором рассматривается движение, можно определить коэффициент пропорциональности A′. Интегрирование по x дает непосредственно множитель a, поэтому

В этом выражении доля dN / N отличается от прежней (2.260), хотя и записана в той же форме: это доля молекул, движущихся вдоль отрезка a со скоростями в

1Многомерного пространства координат и импульсов, в котором состояние молекулы или системы молекул изображается точкой.

2Рассмотрение конкретных способов проведения тех или иных математических действий выходит за рамки настоящего изложения, так как является предметом высшей математики.

121

Х и м и ч е с к а я к и н е т и к а

представляющее собой закон распределения молекул по скоростям при одномерном движении. Отношение dN / N в (2.263) можно рассматривать как веро-

ятность того, что скорость наугад взятой молекулы будет лежать в пределах от

1 dN , скорость ко-

N dx

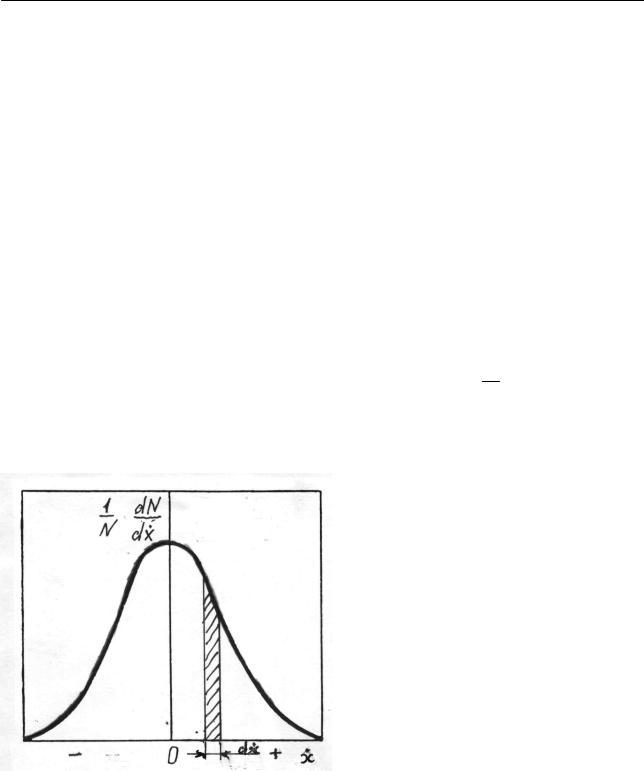
торых лежит в пределах от x до x +1 представлен на рис. 2.31. Наиболее веро-

ятная скорость равна нулю, и доля молекул уменьшается симметрично с увеличением скорости в обе стороны. Доля молекул dN / N со скоростью, лежащей

122

Х и м и ч е с к а я к и н е т и к а

Закон распределения (2.263) позволяет определить среднюю скорость дви-

жения молекул в одном направлении. Она находится путем суммирования абсолютных значений скоростей всех молекул и деления суммы (интеграла) на общее число молекул:

При трехмерном движении вероятность того, что молекула будет иметь скорость в пределах x и x + dx, y и y + dy, z и z + dz , выражается произведени-

ем трех одинаковых вероятностей вида (2.263)

где С – полная скорость молекулы в объеме (C2 = x2 + y2 + z2 ). Не приводя

вывода отметим, что доля молекул, скорости которых лежат в пределах от С доC + dC независимо от направления, определяется уравнением Максвелла для распределения молекул по скоростям

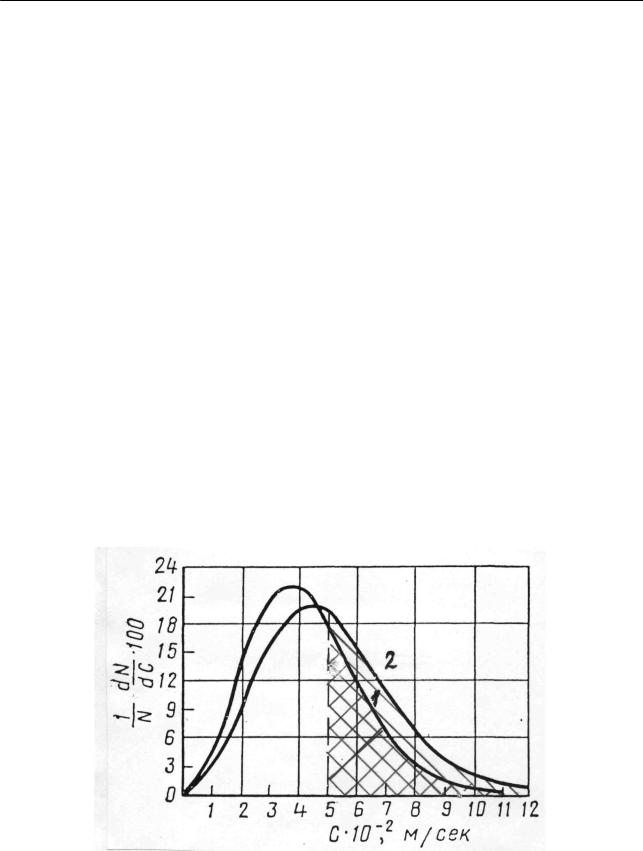
Кривые зависимости от С доли молекул, скорости которых лежат в пределах от С до С + 1, при двух температурах приведены на рис. 2.32. Как видно, кривые

Рис.2.32. Кривые распределения молекул кислорода по скоростям для двух температур:

1 – T = 273 K , 2 – T =373 K

123

Х и м и ч е с к а я к и н е т и к а

проходят через максимум, смещающийся при повышении температуры в сторону бóльших скоростей. Это означает, что с повышением температуры увеличивается число молекул, движущихся с повышенными скоростями. Действительно, как наглядно видно из рис. 2.32, площадь, лежащая под кривой и огра-

ниченная слева ординатой (например, ординатой, отвечающей C =5 102 м/ с), равная доле молекул, скорость которых превышает значение C =5 102 м/ с (заштрихованная область), больше для кривой 2 (T =373 K ),чем для кривой 1 (T = 273 K ). Максимуму на кривых соответствует наиболее вероятная ско-

Для нахождения средней скорости движения молекул при данной температуре умножим dN / N из (2.267)на С и проинтегрируем от нуля до бесконеч-

ности:

Для определения средней квадратичной скорости сначала вычислим

средний квадрат скорости C2 :

извлекая квадратный корень из которого, найдем среднюю квадратичную скорость:

Таким образом, найденные средние скорости различаются по величине и располагаются в следующей последовательности: u >C >б.

Кратко рассмотрев основные вопросы, связанные с распределением молекул по энергиям и скоростям, остановимся на некоторых моментах, касающих-

124

Х и м и ч е с к а я к и н е т и к а

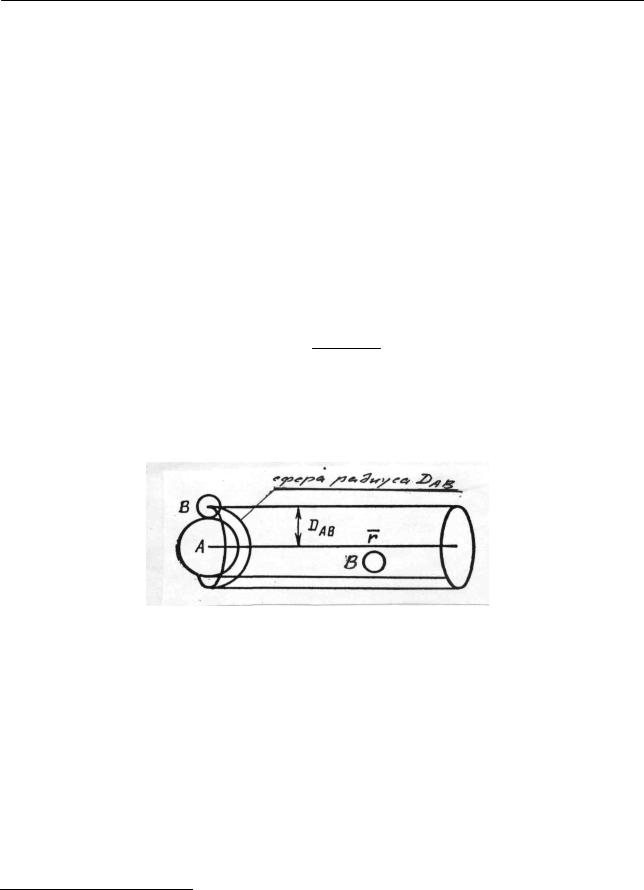
ся межмолекулярных столкновений. В первую очередь условимся, что же именно будем называть столкновением. Дело в том, что, строго говоря, молекулы не имеют определенных размеров, так как плотность электронных облаков нигде не становится равной нулю. Однако такое представление не позволяет даже определить само понятие соударения. Поэтому обычно используют грубую модель, уподобляя молекулы жестким сферам различных диаметров. Рассмотрим в рамках такой модели смесь газов, состоящих из молекул типа А и типа В, массы которых mA иmB , а диаметры – DA и DB соответственно. Столк-

новение (соударение) определим как событие, когда осуществляется контакт двух воображаемых сфер. Для расчета числа соударений молекулы А представим ее движущейся в произвольном направлении со средней относительной скоростью r в то время, как молекулы В будем считать неподвижными. Соударение произойдет в том случае, если центр молекулы В расположен на расстоянии не превышающем

DAB = DA +2 DB

от линии движения молекулы А (рис. 2.33). Общее число соударений в секунду молекулы А с молекулами В равно произведению объема, описываемого за секунду сферой радиуса DAB , на nB – число молекул В в единице объема1.

Входящая в это выражение площадь πDAB2 называется сечением столкнове-

ния, а величина DAB – средним газокинетическим диаметром столкновений

или средним эффективным диаметром столкновений. Для молекул одного вида используют эффективный или газокинетический диаметр D, учиты-

вающий взаимодействие между сталкивающимися молекулами.

1 В СИ единица измерения концентрации ni = N i / V , выраженной числом молекул в единице объема, – м−3 .

125

Х и м и ч е с к а я к и н е т и к а

Значение r определяется выражением, похожим на выражение (2.269) для

C , но масса одной молекулы m заменяется в этом случае приведенной массой двух молекул:

Таким образом, средняя относительная скорость движения молекул А и В

1/ 2

r = 8πµkT . (2.275)

Понятно, что в случае одинаковых молекул mA = mB = m и = m / 2, а, следовательно,

r = 21/ 2 C .

Подставляя выражение (2.275) в (2.273) получим окончательное выражение

для числа столкновений молекулы А с молекулами В за 1 с, т.е. частоту столкновений:

В правой части данного равенства вместо масс молекул в кг , входящих в выражение (2.274) для , введены молярные массы М в кг/моль, а постоянная

Больцмана k заменена, соответственно, газовой постоянной R.

Особо следует остановиться на вопросе используемых единиц измере-

ния. Исходя из того, что средняя относительная скорость движения молекул r (выражения в квадратных скобках соответствуют πr ) включает R илиk , еди-

здесь и в других формулах, включающих среднюю относительную скорость движения молекул, все величины должны быть выражены в системе СИ.

Из соотношения (2.276) следует, что при стандартных условиях (1 атм и

298 К) молекула газа испытывает около 1010 столкновений в секунду. Выраже-

ние (2.276) позволяет также определить среднее время между столкновения-

ми τ как обратную величину числа столкновений одной молекулы в секунду:

126

Х и м и ч е с к а я к и н е т и к а

составляющее при стандартных условиях порядка 10−10 с, и среднюю длину свободного пробега λ , т.е. пути, проходимого молекулой А между двумя

столкновениями. Вычисляется λ путем деления средней скорости CA (2.269) на τ (2.277) , а, следовательно,

торого каждое соударение считалось бы дважды. Таким образом:

Рассмотрение числа двойных столкновений ограничим случаем, когда энергия сталкивающихся молекул сосредоточена лишь в двух степенях свободы или, точнее говоря, выражена двумя квадратичными членами. Такой подход достаточен для решения многих задач химической кинетики. Так, например, при столкновении двух молекул достаточно учитывать лишь относительную кинетическую энергию движения вдоль линии, соединяющей их центры. Сказанное, во-первых, означает, что отсчет скоростей молекул ведется относительно неподвижного центра массы (относительные скорости), а, во-вторых, что берутся не полные относительные скорости, но лишь их составляющие вдоль линии центров, которые и определяют скорость сближения молекул. Обозначив эти составляющие через v′A иvB′ , запишем относительную кинетическую

энергию R вдоль линии центров в следующем виде:

Вычислим число столкновений, происходящих при R, равном или превышающем некоторое критическое значение Е, т.е. при условии R ≥ E .

127

Х и м и ч е с к а я к и н е т и к а

Две сталкивающиеся молекулы рассмотрим как единую систему, обладающую всего двумя степенями свободы1 – по одной на каждую молекулу, что допустимо, так как во внимание принимается только движение вдоль линии центров. Следовательно, можно ограничиться рассмотрением двумерного движения и найти число частиц, т.е. число пар сталкивающихся молекул, которые обладают в двух степенях свободы энергией, не меньшей Е. При двух степенях свободы будем рассматривать движение вдоль координат x и y2. Аналогично рассмотренному ранее более сложному случаю движения в трехмерном пространстве [cм. выражение (2.266)], соответствующий закон распределения за-

пишется как произведение двух выражений, подобных (2.263), т.е.

где С – полная двумерная скорость (C2 = x2 + y2 ) Не приводя вывода отметим,

что закон распределения, выражающий долю частиц, двумерная скорость которых независимо от направления лежит в пределах от С доC + dC определяется уравнением

εдо бесконечности, найдем долю молекул, энергия которых равна или больше

ε:

1В более общем случае, как уже упоминалось, говорят о выражении энергии двумя квадратичными членами, примером чего является соотношение(2.281).

2Математически такой способ рассмотрения вполне эквивалентен движению двух частиц вдоль одной координаты.

128

Х и м и ч е с к а я к и н е т и к а

Выражение (2.286) является единственным случаем в кинетической теории

газов, когда доля молекул просто равна больцмановскому множителю e−ε / kT и, что более важно, будучи полученным для двух степеней свободы поступательного движения, сохраняет свое значение для любого случая, когда энергия выражается двумя квадратичными членами. Так, исходя из того, что энергию гармонического колебания можно представить в виде двух квадратичных членов, соответствующих потенциальной и кинетической энергиям, соотношение (2.288) может также выражать число двухатомных молекул NE с энергией ко-

лебания, равной или большей Е.

Ранее нами было определено общее число двойных столкновений ZAB или Z [соотношения (2.279) и (2.280)], среди которых NE , исходя из вы-

шеизложенного, можно рассматривать как число соударяющихся пар молекул,

которое выражает число двойных столкновений молекул, происходящих с энергией, равной или большей Е, при том условии, что энергия выражается двумя квадратичными членами1.

2.2.2.2.Анализ зависимости влияния температуры на скорость реакции

спозиции кинетической теории газов

Расчет влияния температуры на скорость реакции по правилу Вант–Гоффа, проведенный по уравнению (2.224), показывает очень резкое возрастание ско-

рости реакции при повышении температуры. Так, даже при низких значениях температурного коэффициента скорости реакции (γ = 2), повышение темпера-

туры от 273 K до 373K приводит к повышению скорости реакции в ≈103 раз.

Объяснить столь резкое увеличение скорости реакции при повышении температуры одним только увеличением числа соударений между частицами исходных веществ за счет установленного кинетической теорией газов увеличения числа молекул, движущихся с повышенными скоростями (см рис. 2.32), нельзя. Действительно, в газе при давлении 1 атм скорость, с которой происходят столкновения (частота столкновений) Z (2.279), (2.280) равна приблизи-

1 Строго говоря, ZE представляет собой число столкновений с энергией большей Е при ее удовлетворении данному условию.

129

Х и м и ч е с к а я к и н е т и к а

тельно 1036 c−1 м−3 даже при комнатной температуре. Если бы наличие столкновений было бы единственным фактором, необходимым для протекания реак-

ции, то все газовые реакции заканчивались бы за 10−9 c, но это не так. Более того, частота столкновений зависит от квадратного корня из температуры [уравнения (2.279), (2.280)], и поэтому, предсказывая абсурдно неверную скорость,

мы также предсказываем абсурдно неверную температурную зависимость. Причина наблюдаемого столь резкого увеличения скорости реакции с по-

вышением температуры заключается в том, что для акта химического взаимодействия само по себе столкновение частиц исходных веществ еще недостаточно. Для того, чтобы столкновение было эффективным, т.е., чтобы исходные вещества могли прореагировать, они должны, как известно (см. 2.2.1.6), обладать запасом энергии, равным или большим энергии активации Ea . Число активных

молекул (частиц) NEa , обладающих энергией E ≥ Ea составляет относительно

малую долю от общего числа молекул (частиц) N. Доля молекул, энергия которых равна или больше Ea , исходя из кинетической теории газов, равна множи-

телю e−Ea / RT , аналогичному множителю в распределении Больцмана (посколь-

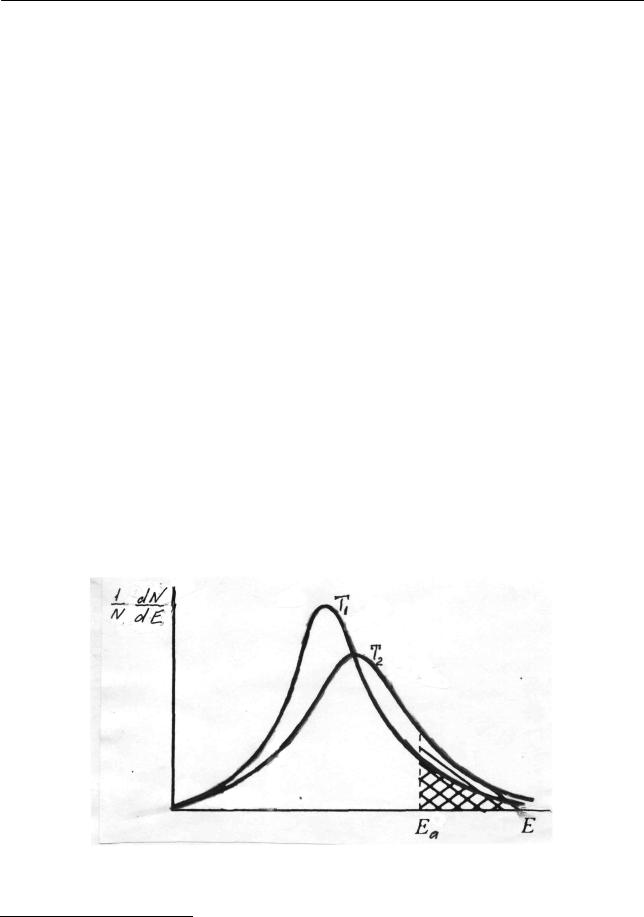
Кривые зависимости от Е доли молекул, энергии которых лежат в пределах от Е до Е + 11, при двух температурах приведены на рис. 2.34. Как видно, кривые

Рис.2.34. Распределение молекул по энергиям (T2 >T1 )

1 Принцип анализа этих кривых аналогичен анализу кривых, приведенных на рис. 2.32. 130