3. Елементи інтегрального числення

1.3.1. Первісна.Невизначений інтеграл

У багатьох практичних задачах потрібно вміти знахо­ди­ти функціюf (x)за її похідноюf ' (x), тобто виконати дію, обернену до диференціювання. Наприклад:

– знайти закон, за яким змінювалась швидкість υ(t),якщо залежність прискорення від часуa(t)відома. Зрозу­міло, що шуканою функцією буде така υ(t), для якої виконується формула;

– знайти закон руху s(t) матеріальної точки за відомою залежніс­тю швидкості від часуυ(t) .

Функція F(x)називаєтьсяпервісноюдля функціїf (x), як­щоF(x)має своєю похідною функціюf (x)(або своїм ди­фе­ренціаломf (x)dx):

F'(x) = f (x).

Теорема про існування первісної. Кожна неперервна функція має нескінченну кількість первісних, які відрізня­ються одна від одної на постійний доданок.

Визначення.Сукупність усіх первіснихF(x) + Cдля даної функ­ції f (x)називається невизначеним інтегралом функціїf (x).

Символ невизначеного інтеграла:. Згідно з оз­на­чен­ням

,

де f (x)– підінтегральна функція,f (x)dx– підінтегральний вираз, – знак інтегралу,x– змінна інтегрування.

1.3.2. Властивості невизначеного інтегралу

1. Постійний множник можна винести за знак інтегралу:

.

2. Інтеграл від алгебраїчної суми скінченного числа функцій дорівнює алгебраїчній сумі інтегралів від цих функ­цій:

.

3. Похідна від невизначеного інтегралу дорівнює під­інтеграль­ній функції:

.

4. Невизначений інтеграл від диференціалу неперервно дифе­рен­ційова­ної функції дорівнює, з точністю до сталого доданка, самій цій функції:

.

5. Якщо дві функції (або два диференціали) тотожно рівні, то їх первісні можуть відрізнятися лише постійним доданком.

1.3.3. Таблиця найпростіших інтегралів

1. (n  –1)	2.
3.	4.
5.	6.
7.	8.
9.
10.
11.
12.
13.
14.

1.3.4. Основні методи інтегрування

1. Безпосереднє інтегрування– інтегрування, котре про­во­дить­ся за допомогою таблиць без додаткових пере­творень.

2. Метод розкладання. Метод базується на розкладанні підін­тег­раль­ної функції на суму функцій, кожна з яких є табличною.

Приклад:

.

3. Інтегрування підстановкою(заміна змінної).

Зміст цього методу полягає в тому, що в інтегралі робиться заміна змінноїx = f (t), тобто вводиться нова зміннаtза­містьx. Диференціалdx = f'(t)dt. Тоді почат­ко­вий інтеграл перепи­сується у вигляді:

.

Якщо підстановка (заміна змінної) вдала, то другий інтеграл легко береться.

Приклад: .

Зробимо заміну змінної, позначивши ­υ = sinx, тоді dυ = = cosxdx. Шуканий інтеграл при цьому набуває таблич­ного вигляду

.

4. Інтегрування частинами. Розглянемо дві неперерв­ні (дифе­рен­ційовані) функціїu = u(x)iυ = υ(x). Утворимо диференціал добутку цих функцій:

d(uυ) = υdu + udυ.

Звідси

або

. (1.14)

Таким чином, інтеграл зводиться до інтеграла, який часто береться більш просто.

1.3.5.Визначений інтеграл

Розглянемо криволінійну трапецію, яка обмежена гра­фі­ком функціїy = f (x), прямимиx = a, x = bі відрізком[a, b] осіOX.Знайдемо площу цієї трапеції. Для цього розіб’ємо відрізок[a, b]на елементарні відрізкиΔx(див. мал. 1.10). Розглянемо площу заштри­хо­ваної фігури (прямо­кутники з основоюΔx), його площа:

S_i = f (_i)(x_i+1 – x_i) = f (_i) Δx _i.

Загальна площа всіх прямокутників дорівнює сумі

Мал. 1.10.

.

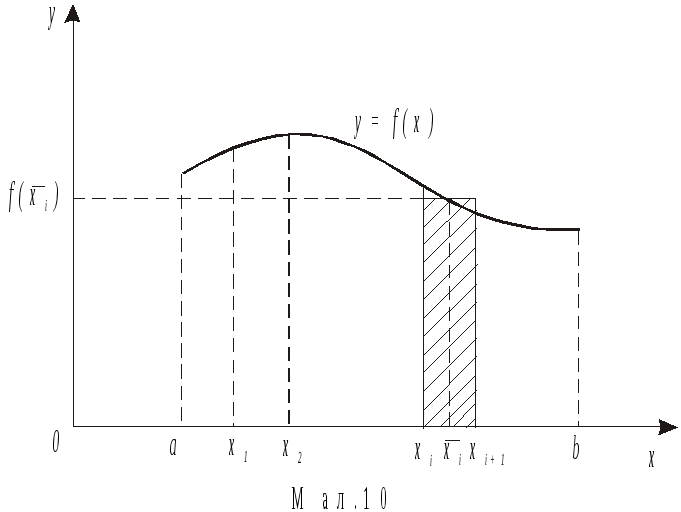
Ця величина буде тим точніше давати пло­­щу криволінійної тра­пе­ції, чим меншеΔx_i. Точне значення площі дається грани­цею:.

Величина називається інтегральною сумою, або сумою Дарбу.

Визначення.Якщо границя інтегральної сумиіснує при всіх, то ця границя нази­ва­єть­­сявизначеним інтеграломвід функціїf (x)на відрізку[а, b] і позначається символом:

,

де a– нижня границя,b– верхня границя,f (x)– підінтег­раль­на функція.