1.5.5. Повторні випробування. Формула Бернуллі

Припустимо, що проводиться декілька випробувань, при­чому ймовірність подіїAу кожному випробуванні не залежить від результатів інших випробувань. Знайдемо ймовірність того, що подія А реалізується рівноmразів у серії зnвипробувань. Ця ймовірність визначаєтьсяформу­лою Бернуллі:

, (1.27)

де p– ймовірність появи подіїАв одному досліді; q = 1 – p– ймовірність того, що подіяА не з’явиться в одному до­сліді; – число можливих комбінацій ізnелементів поm:

.

Зауважимо, що n! (читаєтьсяn-факторіал) дорівнює добутку всіх чисел від 1 доn, тобтоn! = 1234...(n – 1)n.

1.5.6. Випадкова величина,дискретні та неперервні випадкові величини

Статистична обробка медико-біологічних даних базу­єть­ся на використанні методів математичної статистики, основними понят­тя­ми якої є випадкові величини та їх характеристики (математичне сподівання, дисперсія, серед­нє квадратичне відхи­лен­ня, закони розподілу випадкових величин, довірчі інтервали тощо).

Випадковиминазиваються величини, які у результаті випро­бу­вань (вимірювань, спостережень) можуть набувати різних числових значень за однакових умов випробувань. Випадкові величини бувають:

1. Дискретними, тобто такими, які набувають скінченну множину значень і їх можна пронумерувати.

2. Неперервними, тобто такими, які набувають будь-які значення всередині заданого інтервалу.

Розподілом дискретної випадкової величиниXназива­єть­ся множина її можливих значеньX₁, X₂, X₃, ..., X_ni ймовір­ностейP₁, P₂, P₃, ..., P_n, які відповідають цим зна­ченням випадкової величини. Як правило, розподіл випад­кової дискретної величини характеризується таблицею:

Xi	X1	X2	…	Xn–1	Xn
Pi	P1	P2	…	Pn–1	Pn

Зрозуміло, що сума всіх ймовірностей дорівнює 1, тобто .

1.5.7. Інтегральна та диференціальна функції розподілу

Інтегральною функцією розподілу (інтегральним зако­ном розподілу) випадкової величиниХназивається функціяF(x),яка дорівнює ймовірності того,що випадкова вели­чи­на Х прийме значення менше,ніжх:F(x) = P(X < x),де x –дійсне число.

Побудуємо, як приклад, функціюрозподілу дискретної випад­кової величини. Розглянемо однорідний тетраедр, гра­ні якого пронумеровані. Випадкова величинаX, яка дорів­нює кількості очок, що випадають з однаковою ймо­вір­ністю (), може приймати значення: 1; 2; 3; 4.

Очевидно, що на проміжку функція розпо­ділу, оскільки рівною нулю є ймовірність того, що випадкова величинаX прийме значення менше за одиницю (X < x = 1). Імовірність, що X набуде значення менше за 2 , тому на інтервалі (1; 2].Продов­жу­ючи міркування, матимемо:

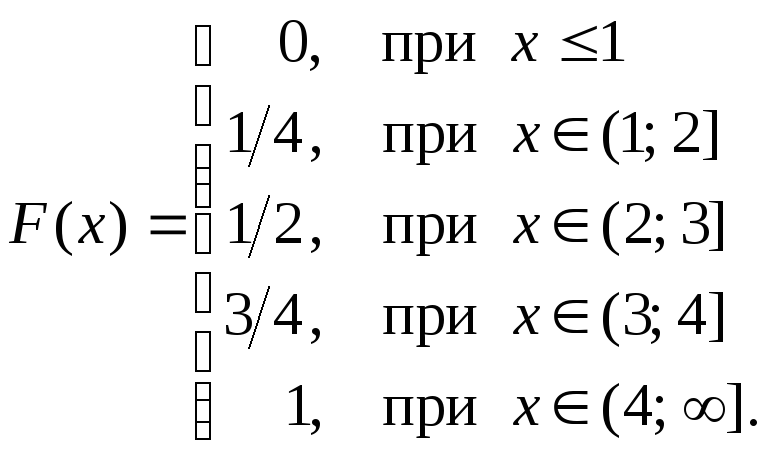
Мал. 1.15.

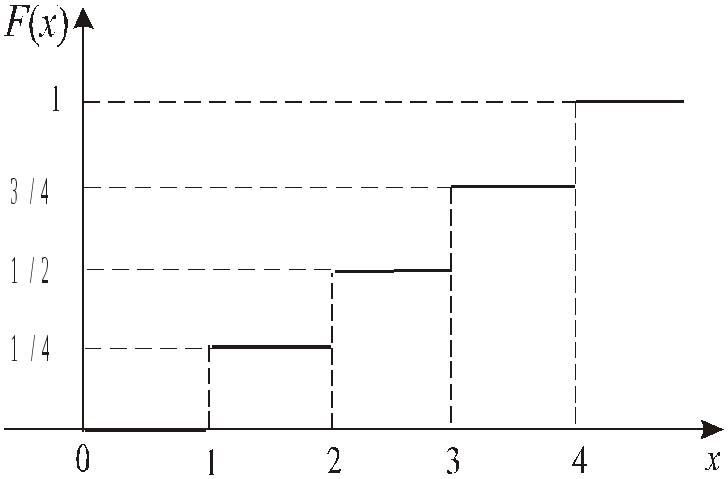
Графік цієї функції подано на мал. 1.15.

Розглянемо основні вла­с­­ти­­вості інтегральної функції розподілу:

1. 0  F(x)  1.

2. F(x) – неспадна функція, тобто, якщоx₁ > x₂, то F(x₁) F(x₂).

3. Ймовірність потрапляння випадкової величини в півінтервал [a;b) дорівнює різниці значень інтегральної функції розподілу на кінцях цього інтервалу: P(a  X < b) = F(b) – F(a).

4. Ймовірність того, що неперервна випадкова величина Х прий­ме будь-яке наперед задане значення, дорівнює нулю:F(X = x₀) = 0.

5. Ймовірність попадання неперервної випадкової величини в інтервал, сегмент і напівінтервал з одними і тими ж значеннями кінців однакова:

P(a < X < b) = P(a  X  b) = P(a  X < b) = P(a < X  b).

6. Якщо всі можливі значення випадкової величини Хналежать деякому інтервалу(a; b), то

F(x) = 0приx  a;

F(x) = 1 приx  b.

В

Мал. 1.16.

ідзначимо, що інтегральна функція розподілу однако­вим чином визначається для диск­ретних і непе­рерв­них випад­ко­вих вели-чин. Для непе­рерв­ної ви­пад­кової величини функ­ція розподілу є непе­рерв­ною і має вигляд, по­діб­ний до зобра­же­ного на мал. 1.16. Графік функ­ції розподілу дис­крет­ної ви­пад­­ко­вої вели­чи­ни має ступін­частий ха­рактер.

Диференціальною функ­цією розподілу (щільністю роз­­по­ділу) називається функціяf (x),яка дорівнює похідній інтег­­раль­ної функції розподілу:

f (x) = F'(x).

Оскільки F(x) – неспадна функція, тоf (x)  0. Поняття диферен­ці­аль­ної функції розподілу вводиться лише для неперервних випадкових величин.

Ймовірність того, що неперервна випадкова величина Х набуватиме значення з деякого інтервалу (a; b), дорівнює визна­че­но­му інтервалу від її щільності розподілу f (x) з межа­ми інтегрування a і b:

.

Г

Мал. 1.17.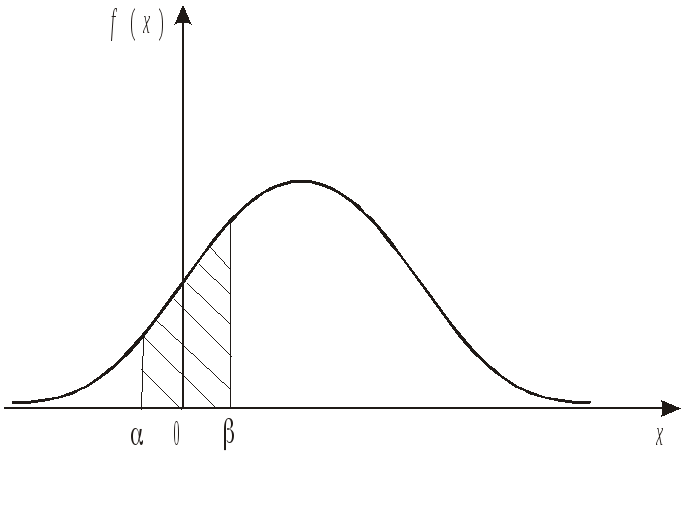

еометричний зміст ці­єї формули очевидний. Ймовірність потрапляння значень випад­ко­­­вої вели­чи­ниXу даний інтервал рівна площі фігури, що обмежена кривою, яка за­дає щільність розподілу, віссю абсцис і прямимиx = a, x = b (мал. 1.17). Безумовно, .