1.5.8. Основні кількісні характеристики розподілу випадкових величин

1. Математичне сподівання абосереднє значенняви­пад­ко­вої величини

. (1.28)

Якщо всі випадкові події рівноймовірні, тобто P₁ = P₂ = = ... , де n– повне число випадкових подій, то в цьому окремому випадку математичне сподівання зводиться до середнього арифметичного:

.

У випадку неперервної випадкової величини .

2. Дисперсія D(X) випадкової величини X

. (1.29)

З формули випливає, що дисперсія – це математичне споді­ван­­ня квадрата відхилення випадкової величини X від її мате­ма­тичного сподівання.

Іншийвираз для дисперсії має вигляд

. (1.30)

Таким чином, дисперсія – це різниця математичного споді­ван­ня квадрата випадкової величини і квадрата матема­тичного сподівання цієї величини.

Для неперервних випадкових величин , деa – середнє значення M(x). Зрозуміло, що дисперсія характеризує відхилення випадкових величин відносно їх середнього значення (матема­тич­ного сподіван­ня). Розмірність дисперсії збігається з розмірністю квадрата величини, яка досліджується. Тому для характеристики відхилення не середнього квадрата, а самої випадкової вели­чи­ни вводиться поняття середнього квадратичного від­хи­лення.

Середнє квадратичне відхилення(X) пов’язане з дис­пер­сією формулою

.

Видно, що розмірність збігається з розмірністю самої ви­пад­кової величиниX.

1.5.9. Основні закони розподілу випадкових величин

Біноміальний розподіл. Припустимо, що проводитьсяnнезалежних випробувань, у кожному з яких може реалізу­ва­тись подіяА, ймовірність появи якоїpпостійна у всіх випробуваннях (імовірність непояви подіїA: q = 1 – p). Роз­гля­немо як дискретну випадкову величинуХчисло появ подіїАу цих випробуваннях. Оскільки подіяАу ви­про­буваннях може не з’явитись або з’явитись 1 раз, або 2 рази, …, абоnразів, то можливими значеннямиХє: 0, 1, 2, 3, …,nвипробувань. Імовірнос­ті цих значень визначаються формулою Бернуллі (1.27):

,

де p– ймовірність появи подіїАв одному досліді; q = 1 – p– ймовірність того, що подіяА не з’явиться в одному до­сліді; – число можливих комбінацій ізnелементів поm:

.

Отже, біноміальним називають розподіл імовірностей, які визначаються формулою Бернуллі. Подамо його у вигля­ді таблиці:

X	0	1	…	m	…	n
P	qn		…		…	pn

Математичне сподівання випадкової величини Х, розпо­ді­ле­ної за біноміальним законом, дорівнює

.

Дисперсія, а, значить,.

Біноміальному розподілу підпорядковуються такі ви­пад­ко­ві події, як виклик швидкої допомоги, число операцій, ріст бактерій, деякі характеристики епідемій тощо. Якщо число дослідів велике, то обчислення ймовірностей за фор­му­лою Бернуллі громіздкі, тоді використовують пуас­со­нів­ське наближення.

Розподіл Пуассона(для рідкісних подій). Для визна­чення ймовірності того, що подія, ймовірність якої мала (), відбудетьсяkразів у серії зnвипробувань (n –достатньо велике), використовують формулу Пуассона:

, (1.31)

де  = np– середнє значення числа випадків, в яких реалі­зується дана подія. Це наближення є особливо вдалим, коли ймовірність подіїАневелика, тому формулу Пуассона часто називають законом рідкісних подій.

Говорять, що випадкова величина Хрозподілена за зако­ном Пуассона, якщо ця величина задана таблицею:

X	0	1	2	3	…
P					…

Розподіл Пуассона використовується у теорії масового обслуговування, теорії надійності, у проблемах використан­ня медичної апаратури тощо.

Математичне сподівання дискретної величини Х, розпо­ді­леної за законом Пуассона, дорівнює

.

Дисперсія

= .

Н

Мал. 1.18.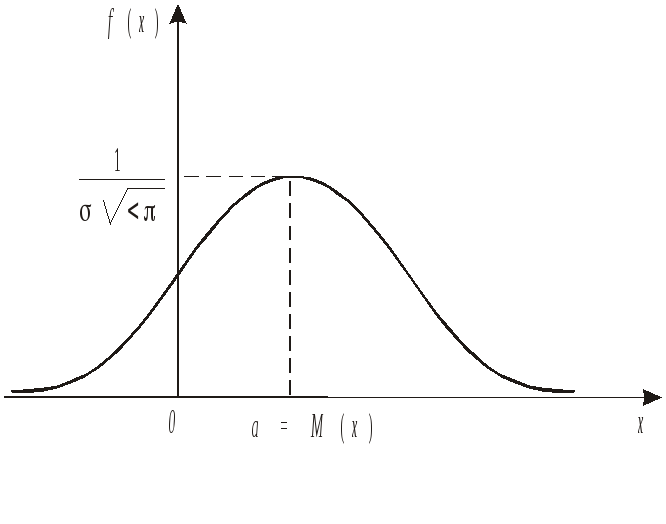

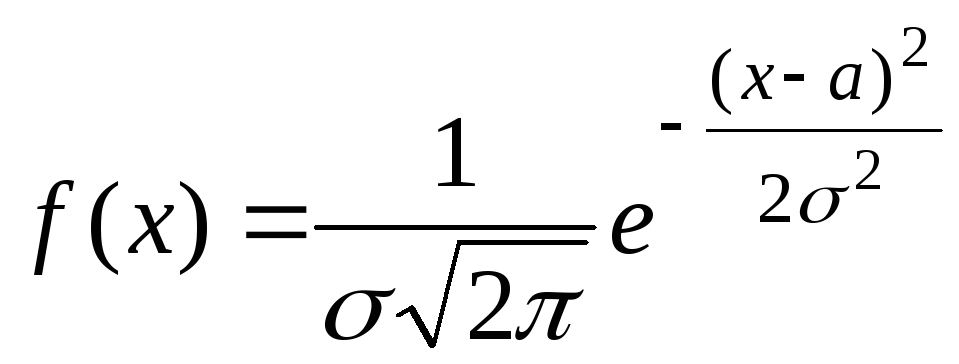ормальний розподіл (розподіл Гаусса). Закон розподілу неперервної випадкової вели­чи­ниХназивається нормаль­ним, якщо щільність розподілу дорівнює:

. (1.32)

Графік розподілу Гаусса описується симетричною від­нос­­но a = M(Х)кривою (див. мал. 1.18),має зміст се­ред­ньоквадра­тич­­­но­­го відхилення . Приx = aорди­ната кри­вої нормальної густини ймо­вір­ності дорів­нює.

При зменшенні ця ордината необмежено зростає. При цьому крива пропор­ційно витягуєть­ся вздовж осі ординат, так що її площа залишається рівною одиниці (мал. 1.19). Іншими словами, “розкид”можливих значень випадкової величини зменшу­ється при зменшенні.

Нормальний розподіл з параметрами a = 0та = 1на­зи­ваютьнормованим. Щіль­ність розподілу в такому ви­пад­ку дорівнює

.

Нормальному закону під­по­рядковується розподіл таких величин, як ріст, вага, арте­ріаль­ний тиск, дов­жи­на су­дин, частота сер­це­вих ско­ро­чень тощо.

П

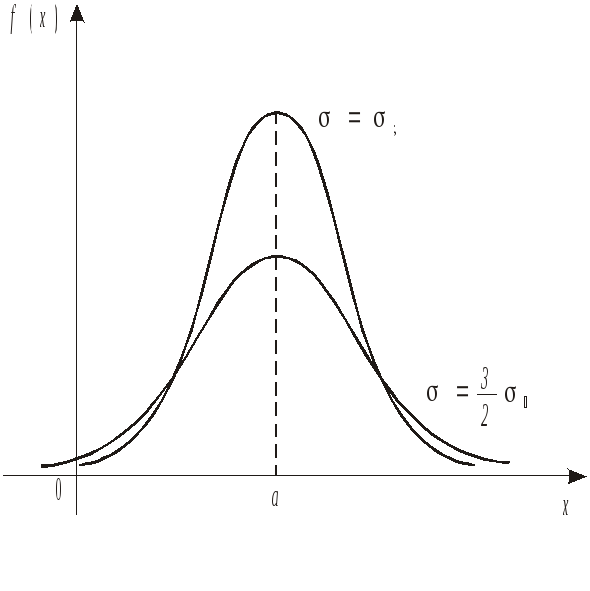Мал. 1.19.

ояснити причини знач­но­го поширення нор­маль­­­­ного закону вперше вда­лось Ляпу­нову. Він по­ка­зав, що якщо випад­кова величина може роз­гля­датись як сума велико­го числа маленьких до­дан­ків, то при достатньо загальних умовах закон роз­по­ділу цієї випадкової вели­чи­ни близь­кий до нормального незалежно від того, які закони розподілу окремих доданків.А оскільки практично всі випад­кові величини є результатом накладання великого числа різних причин, то нормальний закон є найбільш поширеним законом розподілу.

Припустимо, що випадкова величина розподілена за нормаль­ним законом. Тоді ймовірність того, що Хнабуде значення з інтервалу (, ), дорівнює

. (1.33)

Той факт, що нормальний закон розподілу повністю опи­сується математичним сподіванням M(Х) = aі диспер­сі­єю випадкової вели­чи­ниD(Х),дозволяє перетворити вираз (1.33) таким чином, щоб можна було користуватись гото­ви­ми таблицями:

Ф() –Ф() =Ф(t₂) –Ф(t₁). (1.34)

Функція Ф(Х)називаєтьсяфункцією Лапласа, за її допомогою можна знайти ймовірність потрапляння значень нормально розподіленої випадкової величини у будь-який відрізок(, )числової осі. Для функції Лапласа складені таблиці, схожі з широко відомими таблицями логарифмів чи тригонометричних функцій.