Лінійні диференціальні рівняння першого порядку

Диференціальне рівняння першого порядку має загаль­ний вигляд:

F(х, у, у') = 0абоy' = f (х, у). (1.17)

Загальний розв’язок такого рівняння має вигляд:

y = f (x) + C,

де C– деяка константа. Такий розв’язок ще називають загальним інтегралом диференціального рівняння першого порядку.

Загальний інтеграл з визначеним числовим значенням константи Сназивається частинним розв’язком диферен­ці­аль­ного рівняння.

Справедлива теорема про існування єдиного частинного розв’язку диференціального рівняння y' = f (х, у).

Теорема:якщо функція f (х, у) і її частинна похідна не­перервні у деякій області, то існує в даній області єдиний розв’я­зок у =  (х) цього рівняння, для яко­го справедливо: якщо x = x₀, то y = y₀.

Геометричний зміст цієї теореми полягає в тому, що існує, і причому єдина, функція , графік якої прохо­дить через точку ().Умова, згідно з якою прих = х₀функціяyповинна бути рівною y₀, називаєтьсяпочатковою умовою. Початкова умова дозволяє визначити константуС і знайти частинний розв’язок диференціального рівняння.

1.4.3. Диференціальні рівняння зі змінними,що розділяються

У рівнянні (1.17)y' = f (x, y)запишемоy'через відно­шен­ня ди­фе­­рен­­ці­а­лів

.

Такому рівнянню можна надати вигляду:

. (1.18)

Припустимо, що M(x, y)таN(x, y)можна подати добут­ка­ми:

, ,

в яких співмножники залежать лише від однієї змінної. Тоді рівнян­ня (1.18) запишеться у вигляді

dx+dy = 0. (1.19)

Поділивши почленно на добуток (вважа­ємо, що він не дорівнює нулю), одержимо:

dx+dy = 0.

Змінні xiyрозділені. Рівняння можна інтегрувати. Рів­нян­ня (1.19) називається рівнянням із змінними, які розділя­ються. Воно може бути приведеним до рівняння з розділе­ними змінними шляхом ділення на добуток. Цю процедуру називаютьрозділенням змінних. Загальний інтег­рал такого рівняння має вигляд:

F₁ (x) + F₂ (y) = C,

F₁ таF₂– первісні для функційтавідповідно. З використанням початкової умовиx =x₀, y = y₀можна отри­ма­ти частинний розв’язок цього рівняння:

F₁(x) + F₂(y) = F₁(x₀) + F₂(y₀).

Розглянемо розв’язування лінійних диференціальних рів­нянь на прикладі різних фармакокінетичних моделей.

Приклад 1.Розв’язати рівняння, яке описує процес розчинення лікарського препарату в організмі (однокамерна лінійна фармакокі­не­тична модель):

,

де m– маса преперату в момент часуt, k – константа елімінації.

Розв’язок.Враховуючи, що, отримаємо

dm= – kmdt,

або, розділивши змінні,

dm/m = – kdt. (1.20)

Проінтегрувавши ліву і праву частини, маємо:

ln m = – kt + с або .

Позначивши сталуe^cчерезC, отримаємо загальний роз­в’я­зок рівняння:

.

Щоб визначити константу С, досить задати початкові умови. Наприклад, якщо відомо, що в початковий момент часуt = 0маса препарату дорівнювалаm₀, то константаСдорівнюватиме

,

тобто частинний розв’язок рівняння має вигляд

m (t)= .

Однокамерна лінійна модель адекватно описує процеси, які відбуваються при введенні багатьох лікарських препа­ратів ін’єкцією в кров. Циркуляція крові практично миттєво забезпечує рівномірний розподіл препарату в організмі.

Малюнок 1.11 показує, як з плином часу змінюється ма­са і, відповідно, концентрація лікарського препарату у двох су­б’єк­тів з різними зна­чен­нями постійної елімінації (); початкові масиm₀в обох ви­пад­­ках однакові. Постійна елімінації є величиною оберненою до про­­­міжку часу, за який маса препарату в крові зменшується вe2.7 рази і є важливою суб’єктивною характеристикою організ­му.

М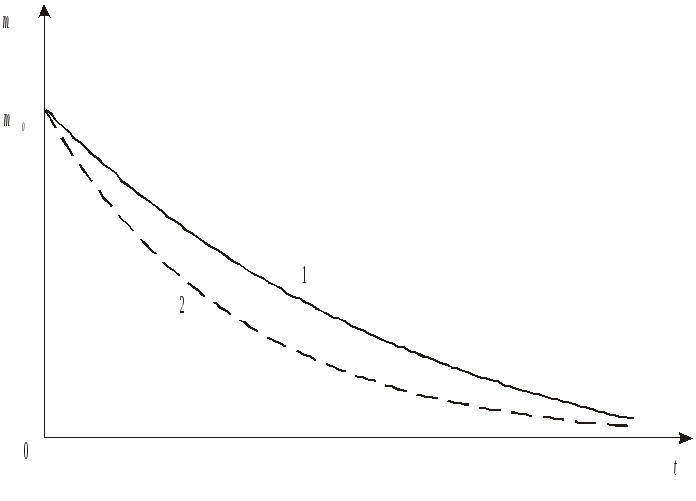ал. 1.11.