47.Определение линейного пространства. Примеры.

Пусть Р – произвольное числовое поле.

Определение 1: множество Vназывается линейным пространством над полем Р, а его элементы –векторами, если: а)задан закон(операция сложения) по которому любым двум элементам x, y из V ставятся в соответствии третий элемент изV называемый их суммой и обозначаемый .

б)задан закон (операция умножения на число), по которому x изV и числу α из Р ставится в соответствии элемент изV называемый произведением x и α и обозначаемый .

в)для любых принадлежащихV и любых α, β принадлежащих Р выполняются следующее требования аксиомы.

1⁰)x+y=y+x

2⁰)(x+y)+z=x+(y+z)

3⁰)Существует элемент Θ ,такой что для любых X принадлежащих V выполняется равенство x+ Θ =x

4⁰)для любых X принадлежащих V существует –x принадлежащий V такой что x+(-x)= Θ

5⁰)α(x+y)= αx+ αy

6⁰)(α+ β)x= αx+βx

7⁰)α( βx)= (αβ)x

8⁰)1*x=x

Вектор –Х называется противоположным вектору Х, вектор Θ - нулевым вектором.

Определение 2:разностью элементов (векторов) Х и Y называется вектор Z, такой что . Обозначается.

Из этого определения следует что элементы (вектора) линейного пространства можно переносить из одной части равенства в другую изменяя знак.

Примеры линейных пространств:

1) пространство V₃- совокупность направленных отрезков (векторов) в пространстве. Сложение вектора и умножение вектора на число было определено в разделе «Векторная алгебра».

Сумма векторов есть вектор, произведение вектора на число – вектор. Аксиомы 1^{0 –} 8⁰ соответствуют свойствам операций сложения векторов и умножением вектора на число доказанное в разделе векторная алгебра. Таким образом V₃ – с указанными операциями является линейным пространством.

2)Rⁿ - совокупность упорядоченных наборов из n – чисел. Если Таким образом. Выполнение аксиом 1^{0 –} 8⁰ легко проверить. В частности .

Фактически мы имеем дело с элементами пространства Rⁿ в разделе матрицы рассматривая строки (столбцы) матрицы.

3)существуют линейные пространства состоящие из одного элемента. Такое пространство называется нулевым. Единственный элемент по необходимости – нулевой и самому себе противоположен. Операции задаются равенством Θ+ Θ=0, αΘ=0. Обозначение { Θ }.

4)множество непрерывных на отрезкефункций с обычными определениями суммы и произведения на число образуют линейной пространство. При этом Θ - функция тождественно равная 0.

5)R_n(х) многочленов с действительными коэффициентами степени с присоединенным числом 0.

Следствия из аксиом:

1)в линейном пространстве существует единственный нулевой элемент

Доказательство: пусть существует два элемента Θ₁ и Θ₂, это значит что (Ч. Т. Д.)

2)в линейном пространстве каждый вектор имеет единственный противоположный.

3)для любого х принадлежащего V имеет место равенство

4)для любого α принадлежащего P имеет место равенство αΘ=Θ

5)если αх=Θ,то или α=0, или х=Θ

6) для любого х принадлежащего V имеет место равенство

7)существует и единственна разность , то есть существует единственный вектор х, который удовлетворяет условию.

8)1.

2.

9)1.

2.

48. Определение линейной зависимости и линейной независимости систем векторов линейного пространства. Определение линейного пространства размерности n и базиса этого пространства. Доказать, что любой вектор линейного пространства можно единственным образом разложить по базису.

Пусть P произвольное числовое поле, V произвольное линейное пространство над этим полем, х₁,х₂…х_n (*) произвольная система векторов пространства V

Определение: Система векторов (*) называется линейно зависимой если существуют числа ₁₂…_n поля Р не все равные 0 и такие что ₁х₁+₂х₂…_nх_n=0 (2).Если равенство (2) выполняется т. и т. т. к. все _i =0 система называется линейно независимой.

Линейной комбинацией векторов х₁,х₂…х_n называется выражение ₁х₁+₂х₂+…+_nх_n

Примерами линейно не зависимых пространств служат любые 3 некомпланарных вектора, любые 4 вектора из V³ линейно зависимы.

В пространстве Rⁿ линейно не зависимы. ₁е₁+₂е₂…_nе_n=0, означает что ₁=(1,0,0,…,0)+ ₂(0,1,0,…,0)+ _n(0,0,…,0,1)=(0,0,…,0) или (_1,₂…_n)= (0,0,…,0). Следовательно векторы е₁ е₂… е_n линейно независимы.

Теорема. При n >=2 cистема векторов х₁,х₂…х_n линейно зависима т и т т к хотя бы один из векторов этой системы являлся линейной комбинацией остальных.

Определение: Линейное пространство V наз. n-мерным если в нем существует n линейно независимых векторов , а любые (n+1) векторов этого пространства линейно зависимы. Число n-размерность линейного пространства.. Обозначение dimV=n .

Если с линейном пространстве V можно найти любое число линейно независимых векторов, то пространство называется бесконечно мерным. Мы ограничимся только рассмотрением конечно мерных пространств.

Примеры:

1. V₃- в этом пространстве существует 3 некомпланарных(линейно независимых) вектора i,j,k. Любые 4 вектора из V - линейно зависимы, следовательно dimV₃=3

2.Rⁿ – в этом пространстве имеется система n линейно независимых векторов . Докажем что любые (n+1) векторов этого пространства линейно зависимы:. Линейно зависимых векторов х₁,х₂…х_{n +1} означает что можно найти числа ₁₂…_n+1 не все равные 0 и такие что ₁х₁+₂х₂₊…+…_n+1х_{n +1} =Θ (4). Равенство (4) означает . Получим однородную систему линейных уравнений сn+1 неизвестными. Эта система совместна и неопределенна. Значит имеется ненулевое решение, что означает что векторы х₁,х₂…х_{n +1} линейно зависимы. Следовательно dimRⁿ =n.

Базис и координаты.

Определение: В n-мерном пространстве V упорядоченная совокупность n линейно независимых векторов называется базисом пространства V.

Теорема. Любой вектор пространства V можно представить в виде линейной комбинации базисных векторов единственным образом.

Доказательство. Пусть е₁,е₂… е_n- базис пространства V и вектор х принадлежит V.

х,е₁,е₂… е_n­-линейно зависима, т.е. существуют числа ₀,₁…_n не все равные 0 и такие, что ₀х+₁е₁+…_nе_n=0, ₀0 . Докажем единственность предположим противное х=₁е₁+…+_nе_n и х=₁е₁+…+_nе_n Не все _i=_j Θ =(₁-₁)е1+…+(_n-_n)е_n=0. _i=_j по базису можно разложить единственным образом.(ч.т.д.)

Теорема. Если е₁,е₂… е_n линейно независимые векторы пространства V и каждый вектор х из V можно представить в виде линейной комбинации векторов е₁,е₂… е_n , то е₁,е₂… е_n является базисом пространства V.

Примеры: 1. В пространстве V₃ роль базиса могут играть вектора . Тогда координатами вектора х принадлежащегоV₃ будут числа .

2. Возьмем в пространстве Rⁿ в качестве базиса векторы 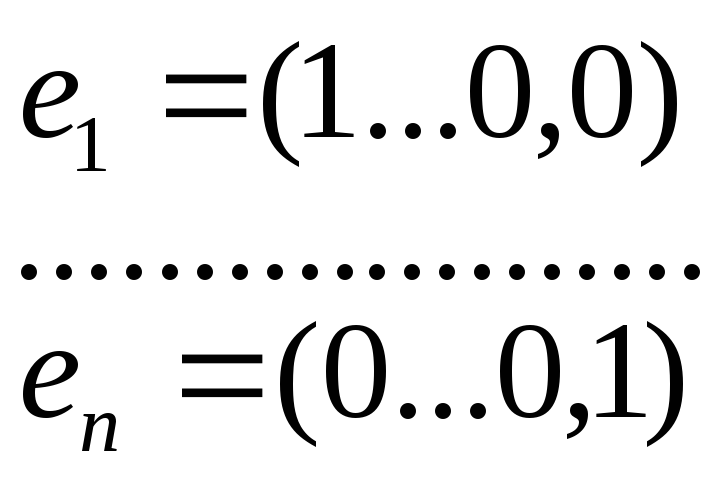. Пусть . Следовательно для вектора х координатами в выбранном базисе являются числа.

Теорема: При сложении векторов их координаты складываются. При умножении вектора на число на это же число умножаются и его координаты.

Переход к новому базису в линейном пространстве. Предположим, что мы имеем два базиса произвольного n – мерного пространства - старый и- новый . Векторы нового базиса разложим по векторам старого:

В матричном виде: - матрица перехода от нового базиса к старому.т.к. в противном случае столбцы матрицы С а следовательно и векторы были бы линейно зависимы, что невозможно.

Обратно: Если то столбцы матрицы С линейно независимы и значит векторыполучающиеся из базисных векторовс помощью матрицы С линейно независимы, т.е. образуют базис.

Таким образом любая квадратная матрица С, у которой может служить матрицей перехода от одного базиса к некоторому другому базису.

Если . Используя (8) легко можно получить формулу.