
ЛЕКЦИИ 2 Версия 3
.pdf
K, максимизирует функцию полезности своего наращенного капитала на некотором финальном T-м шаге.
Вначале мы займемся оценкой инвестиционных проектов с детермини-
рованными результатами. Покажем, что для этой цели применимы базовые ставки дисконта, выбранные указанным выше способом. Пусть инвестор решил участвовать в инвестиционном проекте, и (ϕ0, ϕ1,... , ϕT) — денеж-
ный поток инвестора по данному проекту. Чистые денежные притоки ϕt от проекта изменяют на каждом шаге объем вложений инвестора в ФТ. Соот-
ветственно изменяется значение целевой функции (ожидаемая полезность).
Допустим, что оптимальная политика определена и предусматривает вложения в некоторые оптимальные (вообще говоря, разные на разных ша-
гах) пакеты ФТ, включающие и депозиты/кредиты. (Случайную) брутто-
доходность пакета, в который производятся вложения на шаге t-1 (т.е. от-
ношение доходов, полученных на шаге t, к объему вложений на шаге t-1),
обозначим через θt22. Тогда на финальном шаге капитал инвестора соста-
вит: “ без проекта” — Kθ1...θT , а “ с проектом” —
(...((K + ϕ0 )θ1 + ϕ1 )θ2 + ...)θT + ϕT = (K + ϕ0 )θ1...θT + ϕ1θ2 ...θT + ... + ϕT .
Для оценки эффективности проекта сравним ситуации “ с проектом” и “ без проекта”, найдя прирост целевой функции за счет участия в проекте, а
затем — такое изменение начального капитала, которое при отказе от про-
екта даст тот же прирост. Для крупных проектов ничего проще предложить нельзя (к таким проектам мы еще вернемся в конце данного подраздела).
Однако для малого проекта прирост ожидаемой полезности в ситуации “ с
проектом” по сравнению с ситуацией “ без проекта” составит:
22 Мы обозначаем доходности иной буквой, поскольку теперь нижний индекс у нее отражает не номер ФТ, а момент времени, к которому эта доходность относится. В этих обозначениях вложения K на шаге t-1 дадут чистый приток денежных средств Kθt на шаге t.
70

U = M |
{ |
u ( K + ϕ |
)θ …θ |
T |
+ ϕ θ |
…θ |
T |
+ …+ ϕ |
} |
− M u ( Kθ …θ |
T |
) ≈ |
||
|
|
0 |
1 |
1 2 |
|
T |
|
1 |
|
|||||
≈ M{u′( Kθ1 …θT )[ϕ0θ1 …θT + ϕ1θ2 …θT + …+ ϕT ]} = ∑ ptϕt .(5.15), |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
где коэффициент |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
pt |
= M{u′(Kθ1...θT )[θt +1...θT ]} |
|
|
(5.16) |
||||||||
отражает изменение ожидаемой полезности от добавления 1 рубля на шаге t. Его естественно трактовать, как ценность денег для инвестора на этом шаге. Из (5.15) видно, что за счет реализации проекта ожидаемая по-
лезность изменится точно так же, как от увеличения начального (на шаге
0) капитала инвестора на сумму
K = ϕ |
0 |
+ |
p1 |
ϕ + |
p2 |
|
p1 |
ϕ |
2 |
+ …= ϕ |
0 |
+ |
ϕ1 |
|
|
|
|||||||||||
|
|
p0 |
1 |
p1 |
|
p0 |
|
1 |
+ E1 |
||||
|
|
|
|
|
|
|
|
||||||
где входящие сюда базовые ставки дисконта Et,
дения ценности денег, определяются формулой:
E |
t |
= |
pt −1 − pt |
= |
M{θt θt +1...θT u′(Kθ1...θT )}− |
|
|||||
|
|
pt |
|
M{θt +1...θT u′(Kθ1...θT )} |
|
|
|
|
|
ϕ
+ ( + )(2 + ) + …,
1 E1 1 E2
отражающие темпы па-
1. (5.17)
Заметим теперь, что величина K представляет собой сегодняшний (ны-
нешний) детерминированный эквивалент чистых притоков проекта, т.е. его
DEI, исчисленный при (меняющихся во времени) ставках дисконта Et. По-
этому проект будет выгоден инвестору, если такой DEI положителен, а
лучшему варианту проекта будет отвечать большее значение DEI. Это под-
тверждает применимость базовых ставок дисконта для оценки эффектив-
ности малых инвестиционных проектов.
Существенно упростить полученные формулы можно, предположив, что функция полезности — степенная: u(V) = Vq, а случайные доходности ФТ
на разных шагах независимы. Тогда структура оптимального пакета и распределение его доходности не зависят от объема вложений и их можно с самого начала установить для каждого года расчетного периода. При
71
этом доходности оптимального пакета на разных шагах также будут неза-
висимы. В этом случае критерий оптимальности поведения инвестора при-
нимает вид:
U = M{u[V (ω)]}= M[(Kθ1θ2 ...θT )q ]= K q M θ1q ...M θTq max .
Другими словами, оптимальный пакет на каждом шаге должен максими-
зировать полезность чистых денежных притоков от вложений или, что то же, их брутто-доходности. Тем самым многошаговая задача сводится к не-
скольким одношаговым задачам (5.11), рассмотренным выше. При этом в силу (5.16) имеем
pt = qK |
q−1M q−1 |
q−1 |
q |
= qK |
q−1M q−1 |
|
M q−1 |
|
M q |
, |
(5.18) |
||
θ1 |
...θt |
...θT |
θ1 |
|
... |
θt |
|
... |
θT |
||||
что приводит к обобщенной на многошаговые проекты формуле (5.13):
|
|
|
M θq |
|
||||
|
p |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
||
E = |
t −1 |
− 1 = |
|
|
− 1 . |
(5.19) |
||
|
|
|
|
|
||||
t |
pt |
|
M θq −1 |
|
||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
В следующем примере связь между ставкой дисконта и рисками альтер-
нативных вложений удается описать аналитически.
Пример. Инвестор имеет степенную функцию полезности и он может только вкладывать средства на банковские депозиты (но не может держать их “ в чулке”). Имеется n одинаковых банков, предлагающих депозиты по ставке r (проценты по депозиту выплачиваются непрерывно — на вложен-
ную сумму S за время dt выплачиваются проценты rSdt). У всех банков одинаковая интенсивность банкротства λ — за малый отрезок времени dt
банк может обанкротится с вероятностью λdt. Тогда его клиенты получат только долю ε от вкладов, а “ на месте” банкрота возникнет новый банк с такими же характеристиками.
Очевидно, что в данной ситуации инвестору целесообразно каждый раз делить имеющиеся средства между всеми банками поровну. При этом за
72

малый интервал времени dt имеющаяся у инвестора сумма K превратится в
Kθ, где брутто-доходность θ — случайная величина, равная 1+rdt с вероят-
ностью 1-nλdt, и (1-1/n)(1+rdt) + ε/n с вероятностью nλdt (когда один из банков обанкротится).
Тогда, с точностью до малых второго порядка, имеем:
|
q |
q |
|
n − 1 |
|
ε |
|
q |
|
|
n − 1 + ε |
|
q |
|
|
|
|
|
|
|
|
|
|
||||||
M[θ |
|
]=(1 − nλdt)(1 + rdt) |
+ nλdt |
|
|
(1 + rdt) + |
|
|
|
≈ 1 + qr − nλ + nλ |
|
|
dt ; |
|
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
n |
|
|
|
n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n −1+ ε |
q −1 |
|
||
M[θq −1 ]≈ 1+ (q −1)r − nλ + nλ |
|
dt . |
|||
|
|
|
|
||
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Теперь, используя (5.19), находим коэффициент дисконтирования де-
нежных притоков момента t+dt к моменту t :
M[θq ]
M[θq −1 ]
≈ 1 + r
n −1 + ε q −1 n − 1 + ε |
|||||
+ nλ |
|
|
|
|
|
n |
n |
||||
|
|
|
|||
|
|
n − 1 |
+ ε |
q −1 |
|
||
|
|
|
|
||||
− 1 dt = 1 |
+ r − λ(1 |
− ε) |
|
|
|
|
dt . |
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это означает, что “ мгновенная” базовая ставка дисконта здесь будет по-
стоянной во времени и равной
n −1+ ε q −1 |
|
|
||
E = r − λ(1− ε) |
|
|
. |
(5.20) |
|
||||
|
|
|
||
n |
|
|
|
|
Отсюда находим E = r − εq −1(1− ε)λ при n = 1 и E → r − (1− ε)λ при n → ∞.
Таким образом, с увеличением количества банков (усилением конкуренции между банками) и доли возвращаемых при банкротстве средств ε базовая ставка дисконта возрастает. Соответствующая зависимость (5.20) при q = 0,5, r = 0,12 и λ = 0,04 представлена на рис. 5.1. Зависимость базовой ставки дисконта от склонности инвестора к риску q при ε = 0,25, r = 0,12 и
λ = 0,04 представлена на рис. 5.2. Отметим, что при n = 1 (когда у инвесто-
ра нет других альтернативных направлений вложений) и малых ε ставка дисконта становится отрицательной.
73
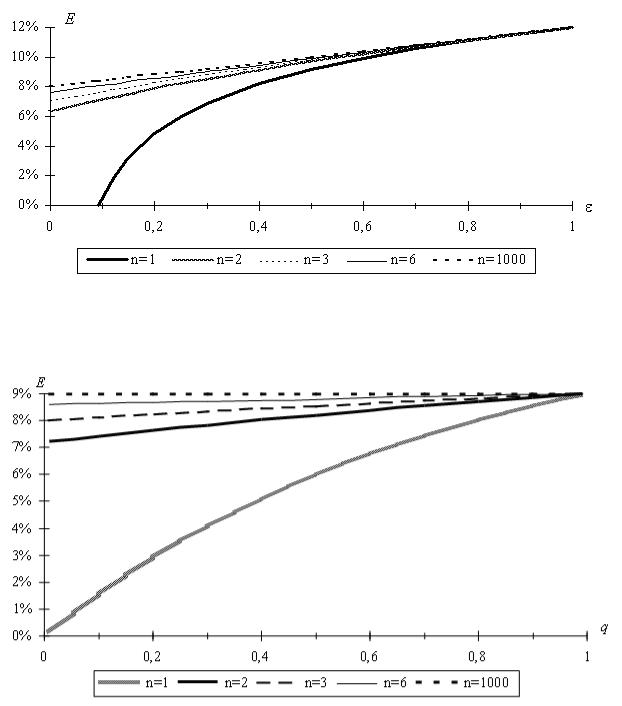
Рис. 5.1
Рис. 5.2
До сих пор речь шла об оценке эффективности детерминированного ма-
лого проекта. Предположим теперь, что чистые доходы проекта случайны,
но не зависят от колебаний курсов ФТ. Здесь уже необходимо рассмат-
ривать более широкое пространство элементарных событий (возможных
“ состояний природы”) Ω, охватывающее как возможные состояния финан-
74
сового рынка, так и возможные состояния других объектов, от которых за-
висят чистые доходы проекта. Соответственно должна расшириться и ве-
роятностная (или — субъективная конечно-аддитивная нормированная)
мера P на Ω. При этом формула (5.15) для прироста ожидаемой полезности от реализации проекта немного изменится и в обозначениях (5.16) примет вид:
U ≈ ∑M[ϕt θt +1...θT u′(Kθ1...θT )]= ∑ pt M[ϕt ], |
(5.21) |
|
t |
t |
|
где символ M теперь означает математическое ожидание соответствую-
щего выражения по новой, расширенной мере P.
Отсюда вытекает, что при реализации такого проекта ожидаемая полез-
ность изменится так же, как и при увеличении начального капитала инве-
|
|
|
1 + E1 |
|
(1 + E1 )(1 + E2 ) |
|
|||
стора на сумму |
M[ϕ |
0 |
]+ |
M[ϕ1 |
] |
+ |
M[ϕ2 ] |
|
+ ..., где ставки дисконта |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
определяются из (5.19). Другими словами, критерием оптимальности здесь становится сумма дисконтированных (при указанных выше ставках дис-
конта) математических ожиданий чистых притоков проекта. Перейдем теперь к общему случаю, когда денежные потоки реального проекта зависят
от конъюнктуры финансового рынка. При этом вначале следует сказать несколько слов о том, в каких случаях такая зависимость может возник-
нуть.
Помимо “ технических” параметров проекта (объем производства про-
дукции и потребления ресурсов, сроки строительства и т.п.), его денежные потоки определяются ценами на разного рода товары и услуги. Поскольку реальные проекты обычно не предусматривают операций на вторичном рынке ценных бумаг, изменение курсов акций на доходах и расходах про-
екта сказаться не должно. Как правило, не возникает риска и при получе-
нии кредита или накоплении средств для финансирования предстоящих расходов (скажем, для образования ликвидационного фонда при разработ-
75

ке нефтяных или угольных месторождений). Однако корреляция между денежными потоками проекта и доходностями ФТ может возникнуть, если на те и другие влияют одни и те же внешние факторы. Например, измене-
ние налоговой или таможенной политики государства может одновремен-
но сказаться и на денежных потоках проекта и на курсах акций многих предприятий, ведущих внешнеторговые операции. Далее, денежные пото-
ки проекта зависят от цен на потребляемые в проекте ресурсы и произво-
димую продукцию. Эти цены, в свою очередь, могут быть скоррелированы с курсами отдельных ФТ. Например, повышение цен на нефть обычно со-
провождается ростом курсов акций нефтяных компаний и вызывает рост цен на топливо, которое может потребляться в данном проекте. Другая си-
туация: падение доходности рыночного пакета акций часто приводит к то-
му, что инвесторы начинают вкладывать средства в землю или недвижи-
мость. Соответственно изменяются цены земельных участков и зданий и плата за их аренду, что может повлиять на денежные потоки конкретного реального проекта.
Поэтому в общем случае в денежных потоках проекта может быть со-
ставляющая, скоррелированная с доходностью каких-то ФТ. Но тогда и весь денежный поток проекта будет скоррелирован с доходностями каких-
то ФТ, а стало быть — и с доходностями оптимального пакета. Здесь при-
рост ожидаемой полезности немного изменится по сравнению с формулой
(5.21).
U ≈ ∑ M[ϕt θt +1...θT u′(Kθ1...θT )]= ∑ |
pt M[ϕt θt +1...θT u′(Kθ1...θT )] =∑ pt E[ϕt ] |
||||||||
|
t |
|
|
t |
M[θt +1...θT u′(Kθ1...θT )] |
t |
|||
где |
E[ϕt |
]= |
M[ϕt |
θt +1...θT u′(Kθ1 |
...θT )] |
. |
(5.22) |
||
M[θt +1...θT u′(Kθ1...θT )] |
|||||||||
|
|
|
|
|
|||||
Отсюда, как и выше, вытекает, что для оценки эффективности проекта рассматриваемого типа можно использовать базовые ставки дисконта
76

(5.17), но дисконтироваться при этом должны не математические ожида-
ния чистых притоков ϕt, а более сложные агрегаты E[ϕt] — детерминиро-
ванные эквиваленты неопределенных чистых притоков от проекта. Таким образом, критерием эффективности проекта здесь будет ожидаемый DEI
—дисконтированная сумма детерминированных эквивалентов чистых
притоков от проекта:
E[ϕ0 ]+ |
E[ϕ1 ] |
+ |
|
E[ϕ2 ] |
|
E[ϕt ] |
|
|
|
(1 + E1 )(1 + E2 ) |
t (1 + E1 )…(1 + Et ) |
. |
(5.23) |
||||
1 + E1 |
||||||||
|
|
|
+ …= ∑ |
|
||||
|
|
|
6. |
Интервальная неопределенность |
|
|||
|
|
|
6.1. |
Критерий оптимизма – |
пессимизма |
|
||
Критерий ожидаемой полезности достаточно широко используется в экономических исследованиях. Но он применим при заданных вероятно-
стях исходов. Между тем в реальных проектах (особенно инновационных)
мы, как правило, имеем дело с другим типом неопределенности, когда нельзя говорить о статистической устойчивости. В этом случае инвестор хотел бы выбрать такую политику вложений F, которая обеспечила бы ему максимальный (наращенный) капитал. Однако при разных состояниях природы23 s стоимость капитала F(s) может быть разной. Поэтому инве-
стор хочет максимизировать как бы все возможные стоимости сразу, т.е.
решает многокритериальную задачу. Однако при этом его совершенно не интересует, при каком именно состоянии природы достигаются те или иные стоимости капитала.
Другими словами, каждую политику вложений F он характеризует не функцией F(s), а только множеством X = XF возможных значений этой функции — некоторым подмножеством числовой оси (каждая из точек X
23 Состояние природы – это окружающая инвестора среда, в частности, - макроэкономическая.
77
может отвечать сразу нескольким значениям s). Тем самым, две политики,
при которых наращенный капитал может оказаться равным, например,
только 10, 20 или 30 (для каждой политики — при каких-то своих состоя-
ниях природы), субъект должен рассматривать как эквивалентные. Такого рода неопределенность, когда инвестор не различает (или не может или не хочет различать) состояния природы, дающие одинаковый результат, названа интервальной. Предполагается, что никакая политика вложений не может дать сколь угодно большого капитала, так что множества возмож-
ных значений капитала X — ограниченные. Максимально- и минимально возможным значениям капитала будут отвечать теперь крайние (гранич-
ные) точки множества X. Мы введем для них специальные обозначения:
M (X ) = sup x, m(X ) = inf x .
x X x X
Детерминированной политике, которая при любом состоянии природы дает один и тот же (наращенный) капитал b, отвечает множество Ib= {b},
состоящее из единственной точки b.
Если инвестор может оценивать политики и выбирать лучшую из не-
скольких альтернатив, это означает, что он оценивает каждую политику по некоторому критерию ожидаемого капитала. В данном случае такой кри-
терий будет зависеть только от соответствующего множества возможных при данной политике значений капитала, т.е. будет функционалом, опре-
деленным на классе ограниченных подмножеств числовой оси. Значение критерия, отвечающее множеству X, обозначим через E(X). Ниже мы уста-
новим вид этого функционала, удовлетворяющего трем довольно простым требованиям (аксиомам).
Прежде всего, хотелось бы, что решения, принимаемые в условиях не-
определенности, были бы согласованы с решениями в детерминированной ситуации. Для этого заметим, что множество Ib= {b}, состоящее из единст-
венной точки b, отвечает детерминированной политике, дающей капитал b,
78
и стало быть, здесь значение ожидаемого капитала тоже должно быть рав-
но b. Это требование выражается следующей аксиомой.
Согласованность. E(Ib) = b при любом b.
Заметим далее, что отношениям между ограниченными функциями на S
отвечают отношения между множествами их возможных значений (обрат-
ное неверно: одному и тому же отношению между множествами могут от-
вечать разные отношения между функциями). Нам понадобятся два из них.
Иногда про одну политику F субъект может сразу же сказать, что она лучше или, по крайней мере, не хуже другой политики G, а, стало быть,
ожидаемый эффект у нее не меньше. Это значит, что между некоторыми
политиками F и G можно установить соответствующее отношение “ явного предпочтения” — доминирования. Так, любой субъект, ведущий себя ра-
ционально, должен считать, что политика F явно предпочтительнее поли-
тики G, если политика G при одних состояниях природы дает такой же ка-
питал, что и F, а при других — меньший, т.е. когда F(s) > G(s) при всех s. В
этом случае для каждого значения капитала x, возможного при политике F,
найдется не большее значение капитала y, возможного при политике G, а
для каждого значения капитала y, возможного при политике G, найдется не меньшее значение капитала x, возможного при политике F. Такому отно-
шению между политиками (функциями от состояния природы) отвечает следующее отношение доминирования множеств.
Скажем, что множество X доминирует множество Y (X » Y), если каждую точку множества X можно получить, увеличивая или не меняя какую-то точку из Y, а каждую точку Y можно получить, уменьшая или не меняя ка-
кую-то точку из X. Это можно сформулировать короче: X » Y, если для лю-
бого x X найдется y Y такое, что y<x, и для любого y Y найдется x X
такое, что x >y.
Следующая лемма выражает простые свойства введенного отношения.
Лемма 6.1.
79
