ЛЕКЦИИ 2 Версия 3

Этот критерий можно обосновать, используя аксиомы7 Неймана – Мор-

генштерна [6].

Здесь Vx — наращенный (за счет вложений в портфель x) капитал инве-

стора в конце шага, u(V) — функция полезности инвестора, которая пред-

полагается возрастающей, равной нулю при V = 0 и выпуклой вверх (т.е. u"(V) < 0). Последнее требование означает, что инвестор не склонен к рис-

ку (“ осторожен”) и придает увеличению капитала меньшую ценность, чем

такому же по величине его уменьшению. Таких инвесторов — большинст-

во на финансовом рынке. Используя (4.1), целевую функцию задачи (4.3)

можно записать иначе:

Таким образом, оптимальный портфель обеспечивает выполнение (4.4)

при естественных ограничениях на начальный капитал инвестора и неот-

рицательность долей всех ФА (рискованные активы только покупаем, но не берем в долг), кроме депозитов:

рассчитывается на все возможные “ завтра” ситуации с учетом их вероят-

ностей, причем рассчитывается так, чтобы случайные последствия приня-

того решения оказались в некотором смысле наилучшими. Обратите вни-

мание, что при этом фирма не назначает себе какого-то целевого уровня завтрашнего собственного капитала и не ставит себе целью достичь этого уровня. Это резко отличает данный подход от рекомендованного в [11],

суть которого хорошо видна из следующей цитаты: “ Стратегические пла-

7 Отношение предпочтения полно, транзитивно, рефлексивно и т.д.

20

ны предприятия разрабатываются в расчете на некоторые фиксированные условия или, по крайней мере, на их более или менее предсказуемое разви-

тие. Вследствие того, что такие предположения часто нарушаются, осо-

бенно в долгосрочной перспективе, всегда остается шанс не достичь наме-

ченной цели, не получить запланированный стратегический результат.

Возможность отклонения от цели стратегического решения, т.е. несовпа-

дение фактически полученного экономического результата с намеченным в момент принятия решений, принято характеризовать с помощью катего-

рии “ хозяйственный риск”. Заметим, что это несовпадение не обязательно бывает в худшую сторону; весьма возможно, что результат превзойдет ожидания. Однако это, скорее, исключение, чем правило. ... Понятие риска используется в этом смысле как характеристика процесса и результата принятия стратегических решений. В таком аспекте риск – это возмож-

ность таких последствий принимаемых стратегических решений, при ко-

торых поставленные цели (генеральная цель предприятия либо стратегиче-

ские цели) частично или полностью не достигаются”. Соответственно да-

лее к факторам риска, существенным “ на уровне принятия руководством стратегических решений”, авторы относят и “ ошибочный прогноз развития внешней для предприятия хозяйственной среды в долгосрочной перспек-

тиве”. По нашему мнению, подобный взгляд на стратегическое планирова-

ние неконструктивен. Основным его отличием от оперативного планиро-

вания является как раз то, что здесь решения не базируются на каком-то одном “ прогнозе развития внешней для предприятия хозяйственной сре-

ды” и не предусматривают конкретных количественных целевых ориенти-

ров, которые должны достигаться “ во всех случаях жизни”.

Переходя к рассмотрению задачи выбора оптимального пакета, отметим два важных обстоятельства.

1. Целевая функция является строго выпуклой вверх функцией от x. Это следует из строгой выпуклости функции u. Действительно, пусть x и y —

21

В частности, если два пакета дают одну и ту же ожидаемую полезность,

то “ объединенный” пакет (а его доходность будет полусуммой доходно-

стей обоих пакетов) обеспечит получение большей ожидаемой полезно-

сти.

Таким образом, мы имеем дело с задачей максимизации выпуклой вверх функции при ограничениях типа равенств, заданными линейными функ-

циями. Поэтому здесь можно применить известную из выпуклого анализа теорему Куна-Таккера, и выяснить, что пакет x будет оптимальным тогда и

Примечание. Решение задачи устроено очень просто: на переменную x0

не наложено никаких ограничений, поэтому ∂W 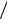∂x0 = 0 , какие-то из вели-

чин xn положительны, тогда соответствующая производная ∂W 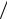∂xn тоже

равна нулю, а все остальные xn = 0 и для них соответствующая производ-

ная ∂W 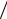∂xn не положительна.

Потребуем теперь дополнительно, чтобы критерий оптимальности U в

нашей задаче зависел только от математического ожидания и дисперсии наращенного капитала:

M[u(Vx)] = f(M[Vx], D[Vx]), где f(M, D) — некоторая гладкая функ-

ция двух переменных,. Это возможно в двух случаях:

А. В диапазоне реального изменения наращенного капитала функция

22

Б. Вектор, образованный случайными доходностями всех ФА, имеет

(многомерное) нормальное распределение. В частности, доходность любо-

го ФА тоже является нормально распределенной случайной величиной.

Действительно, в случае А величина M[u(Vx)] = pM[Vx] - qM[(Vx)2] =

pM[Vx] - qD[Vx] - qM[Vx]2 будет функцией, возрастающей по M[Vx] и

убывающей по D[Vx].

Рассмотрим подробнее случай Б. Здесь Vx = Kξ x = ∑ Kxiξi , являясь ли-

i

нейной комбинацией от компонент нормально распределенного вектора,

сама имеет нормальное распределение, которое определяется только пара-

метрами M[Vx] и D[Vx]. Этими же параметрами однозначно характеризу-

ется и распределение любой функции от нее, в том числе и u(Vx), и мате-

матическое ожидание M[u(Vx)].

Обратим особое внимание, что случай Б имеет место только тогда, когда доходности всех ФА имеют совместное нормальное распределение. Того факта, что каждая из этих доходностей в отдельности имеет нормальное распределение, недостаточно.

Таким образом, здесь M[u(Vx)] будет функцией только от M[Vx] и

Чтобы доказать, что эта функция возрастает по M[Vx] и убывает по т.е. ее производные по этим аргументам соответственно положительные и отрицательные, рассмотрим случай, когда Vx имеет нормальное распределение со средним a и дисперсией σ2. Тогда, обозначив через N(x) — плотность стандартного нормального распределения, имеем:

23

Примечание. Тот факт, что f(M, D) возрастает по M и убывает по D,

представляется совершенно естественным: при сравнении двух портфелей с одинаковыми математическими ожиданиями наращенного капитала фирма, скорее всего, выберет портфель, которому отвечает меньшая дис-

персия, а при сравнении двух портфелей с одинаковыми дисперсиями — тот, которому отвечает большее математическое ожидание. Легко пока-

зать, что лучшее решение задачи с критерием f(M(x),D(x)) является опти-

мальным по Парето для задачи с двумя критериями М(х) максимизиро-

вать, σ(x) минимизировать. Если поделить данные величины на исходный капитал инвестора (весь капитал, а не часть, инвестируется в пакет), то получим традиционную “ портфельную” постановку. Как правило, задачу изначально ставят еще в более “ технической упаковке”: минимизировать риск, σ(x), при заданной доходности. Это один из приемов нахождения точек оптимальных по Парето, эффективных. Нормальность распределе-

ния, как правило, не оговаривается, а принятие среднеквадратичного от-

клонения в качестве меры риска – просто декларируется. Кстати, при та-

ком подходе возникает вопрос: « А почему в качестве меры риска не взять бы отклонения только в худшую сторону? Это же более соответствует бытовому пониманию риска?» Рассмотрение данного вопроса с помощью функции полезности дает ответ: «В случае нормального распределения это возможно, т. к. дисперсия убытков в два раза меньше всей дисперсии».

Нетрудно показать, что кривая безразличия, f (M, D)= const, функция

M(D) является возрастающей и строго выпуклой.

24

Итак, критерии доходность-риск – это результат решения задачи оптимизации всего финансового плана (а не локальной задачи выбора лучшего проекта в рамках одного периода, при этом остальные ресурсы инвестируются в финансовые активы), поэтому они “ не такие” как

NPV.

С учетом изложенного выше, полученное условие оптимальности можно сформулировать иначе: пакет x будет оптимальным тогда и только тогда,

когда при некотором ϑ производные будут равны ϑ, если n = 0 или xn > 0,

и будут не больше ϑ, если n > 0 и xn = 0. Чтобы конкретизировать это ус-

ловие, вычислим указанные производные. Для этого заметим, что в силу

(4.2):

Итак, мы получили, что пакет x будет оптимальным, если и только если

при некотором ϑ будут выполняться соотношения:

25

Поскольку ковариация детерминированной и случайной величин равна нулю, то ci0= c0i= 0 при всех i. Поэтому в соотношениях (4.7) можно сум-

мировать только по n > 0, а первое из этих соотношений становится совсем

простым: Aa0= J. Вычитая это из двух последних соотношений, для i > 0

найдем:

Обозначив h = A/B, полученные соотношения можно записать иначе:

Итак, мы получили, что каким бы ни был оптимальный пакет x (а опти-

мальных пакетов может быть много), его компоненты будут удовлетворять соотношениям (4.9) при некотором положительном h. Заметим теперь, что неизвестная x0 в систему (4.8) не входит. Однако, решив эту систему, мож-

но найти x0 из (4.9):

Учтем теперь, что полученные соотношения являются необходимыми и достаточными для оптимальности пакета x. В общем случае им может удовлетворять не один, а много разных векторов x, но значение целевой

функции для всех этих пакетов будет одно и то же.

Рассмотрим теперь неотрицательные величины yi=xi/h. В силу (4.8) они

будут решениями системы:

Пусть Y — это множество всех решений системы, очевидно, оно – вы-

пукло. Докажем, что в Y найдется вектор w, пропорциональный вектору m,

26

характеризующему структуру рыночного пакета всех рискованных фи-

нансовых титулов, ФТ8. Для этого заметим, что любое решение (4.8) по-

лучается из какого-то решения (4.10) умножением на число h. Поэтому можно считать, что инвестор вначале выбирает какой-то вектор из множе-

ства Y, затем умножает его на h, получая в результате структуру x своего оптимального портфеля рискованных активов, и, наконец, находит долю депозита/кредита из (4.9). Далее, инвесторов на рынке много, и каждому s-

му из них отвечает свое значение hs, свой вектор ys и соответствующий оптимальный пакет рискованных ФТ hsys. Однако все выбранные ys

принадлежат одному и тому же выпуклому множеству Y. Но тогда вектор m, характеризующий структуру рыночного пакета рискованных ФТ, ока-

жется линейной комбинацией hsys с положительными коэффициентами

(зависящими от объемов вложений инвесторов): m = ∑δs hs y s . Положим

нейной комбинацией векторов ys Y, и, значит, будет принадлежать Y.

Учтем теперь, что рыночный пакет содержит все имеющиеся на рынке виды рискованных ФТ, т.е. каждая компонента вектора m, а, значит, и

вектора w, положительна. В этом случае в системе (4.10) будут выполнять-

ся точные равенства:

Но на множестве Q решений системы(4.8)-(4.9) целевая функция любо-

го s-го инвестора принимает одно и то же максимальное значение (исполь-

зуем достаточные условия теоремы К-Т). Поэтому она не изменится, если инвестор заменит использованный в указанной выше процедуре им вектор ys на w. Иными словами, любой инвестор, не ухудшая своего положе-

8 ФТ и ФА – обозначают одно и то же.

27

ния, может заменить свой оптимальный пакет рискованных ФТ другим, имеющим структуру рыночного пакета. Это утверждение известно как теорема разделения Тобина.

В этой связи надо отметить три обстоятельства.

Во-первых, полученное решение действительно носит стратегический характер: в оптимальном пакете должны присутствовать все имеющиеся на рынке рискованные ФТ и в той пропорции, которая сложилась на рынке в момент принятия решения. Склонность инвестора к риску учитывается при этом только отношением объема депозита/кредита к вложениям в рыноч-

ный пакет.

Во-вторых, именно при доказательстве теоремы Тобина модель приоб-

рела “ общерыночный” характер, поскольку здесь мы учли, что:

1)на рынке есть много инвесторов, каждый из которых максимизирует свою функцию ожидаемой полезности;

2)все инвесторы используют одну и ту же информацию о рынке, поку-

пают и продают ФТ по одним и тем же (рыночным) ценам;

3) все инвесторы имеют однородные ожидания (homogeneous expectations), т.е. исходят из одного и то же совместного вероятностного распре-

деления доходностей ФТ, которому отвечают входящие в (4.8) средние значения, дисперсии и ковариации доходностей;

4) спрос на ФТ совпадает с предложением, т.е. сумма рискованных час-

тей оптимальных пакетов всех инвесторов равна общему пакету рискован-

ных ФТ, находящихся в обращении на рынке.

БЕТА-ФОРМУЛА

Из изложенного выше следует, что равенствам (4.11) удовлетворяет век-

тор w = λm. Поэтому имеем:

28

Как правило, средние доходности ФА больше безрисковой (a0). По-

этому, как видно из (4.12), с ростом ковариации cov(ξi, ξm) соответствую-

щее превышение ai- a0 увеличивается. На этом основании величина cov(ξi, ξm)/σm обычно трактуется как мера систематического (рыночный,

рыночная стоимость единицы этого риска, коэффициент Шарпа9. Чтобы найти λ, умножим обе части (4.12) на mi и просуммируем по всем i. Мы получим:

Явление, при котором доходности активов скоррелированы с доходностью рыночного пакета, обычно называют систематическим (или неди-

9 Лауреат Нобелевской премии по экономике.

29