Добавил:

PavelEngineer Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Севастопольский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

[James_Stewart]_Single_Variable_Calculus_Early_Tr(BookFi).pdf

Скачиваний:

Добавлен:

30.12.2019

Размер:

18.09 Mб

Скачать

☆

<<< < Предыдущая 39 40 41 42 43 44 45 46 47 48 49 5051 / 9151 52 53 54 55 56 57 58 59 60 61 62 63 > Следующая >>>

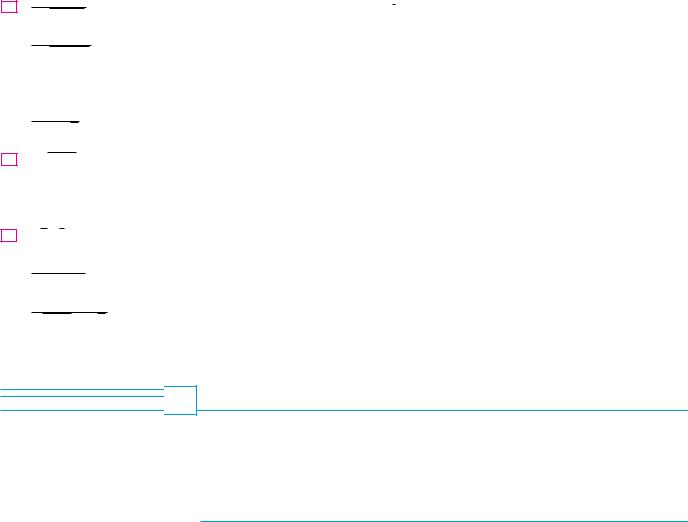
49. y x s4x1 1 dx

51. y x s4x 2 1 dx

53. yx 2 sinh mx dx

55. y x xsx

57.yx s3 x c dx

59.ycos x cos3 sin x dx

61.ysx esx dx

sin 2x

63. y 1 cos4 x dx

65. y sx 1 sx dx

SECTION 7.6 INTEGRATION USING TABLES AND COMPUTER ALGEBRA SYSTEMS |||| 489

50.

x 2 s

4x 1

52.

x x 4 1

54.

y x sin x 2 dx

56.

58.

x ln x

x 2 1

60.

x 2s

4x 2 1

62.

ln tan x

64.

y 4

sin x cos x

u 3 1

66.

u 3 u 2

67.

y1s

1 x 2

68.

x 2

1 2e x e x

ln x

70.

69.

1 e x

x 2

71.

x arcsin x

72.

4 x 10 x

2 x

1 x 2

73.

74.

x 2 x 2 4

(2 s

75.

76.

y x 2 bx sin 2x dx

1 e x

sec x cos 2x

77.

78.

1 x 3

sin x sec x

79.

yx sin2 x cos x dx

80.

sin x cos x

sin4 x cos4 x

81.

The functions y e x2

and y x 2e x2

don’t have elementary

antiderivatives, but y 2x 2 1 e x2 does. Evaluate

x 2x 2 1 e x2 dx.

7.6 INTEGRATION USING TABLES AND COMPUTER ALGEBRA SYSTEMS

In this section we describe how to use tables and computer algebra systems to integrate functions that have elementary antiderivatives. You should bear in mind, though, that even the most powerful computer algebra systems can’t ﬁnd explicit formulas for the antiderivatives of functions like ex2 or the other functions described at the end of Section 7.5.

TABLES OF INTEGRALS

Tables of indeﬁnite integrals are very useful when we are confronted by an integral that is difﬁcult to evaluate by hand and we don’t have access to a computer algebra system. A relatively brief table of 120 integrals, categorized by form, is provided on the Reference Pages at the back of the book. More extensive tables are available in CRC Standard Mathematical Tables and Formulae, 31st ed. by Daniel Zwillinger (Boca Raton, FL: CRC Press, 2002) (709 entries) or in Gradshteyn and Ryzhik’s Table of Integrals, Series, and Products, 6e (San Diego: Academic Press, 2000), which contains hundreds of pages of integrals. It should be remembered, however, that integrals do not often occur in exactly the form listed in a table. Usually we need to use substitution or algebraic manipulation to transform a given integral into one of the forms in the table.

EXAMPLE 1 The region bounded by the curves y arctan x, y 0, and x 1 is rotated about the y-axis. Find the volume of the resulting solid.

SOLUTION Using the method of cylindrical shells, we see that the volume is

V y1 2 x arctan x dx

490 |||| CHAPTER 7 TECHNIQUES OF INTEGRATION

N The Table of Integrals appears on Reference Pages 6 –10 at the back of the book.

In the section of the Table of Integrals titled Inverse Trigonometric Forms we locate Formula 92:

yu tan 1u du

tan 1u

Thus the volume is

V 2 y0 x tan 1x dx 2

tan 1x

[ x2 1 tan 1x x]10 2 tan 1 1 1

2 4 1 21

EXAMPLE 2 Use the Table of Integrals to ﬁnd y

dx.

4x2

SOLUTION If we look at the section of the table titled Forms involving sa2 u2 , we see that the closest entry is number 34:

sin 1

sa2 u2

a2 u2

This is not exactly what we have, but we will be able to use it if we ﬁrst make the substitution u 2x:

dx y

u 2 2

5 4x2

5 u2

Then we use Formula 34 with a2 5 (so a s

sin 1

5 4x2

5 u2

sin 1

5 4x2

8 s

EXAMPLE 3 Use the Table of Integrals to ﬁnd yx3 sin x dx.

85.yu n cos u du

u n sin u n yu n 1 sin u du

SOLUTION If we look in the section called Trigonometric Forms, we see that none of the entries explicitly includes a u3 factor. However, we can use the reduction formula in entry 84 with n 3:

yx3 sin x dx x3 cos x 3 yx2 cos x dx

We now need to evaluate xx2 cos x dx. We can use the reduction formula in entry 85 with n 2, followed by entry 82:

yx2 cos x dx x2 sin x 2 yx sin x dx

x2 sin x 2 sin x x cos x K

SECTION 7.6 INTEGRATION USING TABLES AND COMPUTER ALGEBRA SYSTEMS |||| 491

Combining these calculations, we get

yx3 sin x dx x3 cos x 3x2 sin x 6x cos x 6 sin x C

where C 3K.

V EXAMPLE 4 Use the Table of Integrals to ﬁnd yxsx2 2x 4 dx.

SOLUTION Since the table gives forms involving sa2 x2 , sa2 x2 , and sx2 a2 , but not sax2 bx c , we ﬁrst complete the square:

x2 2x 4 x 1 2 3

If we make the substitution u x 1 (so x u 1), the integrand will involve the pattern sa2 u2 :

yxsx2 2x 4 dx y u 1 su2 3 du

21. ysa 2 u 2 du u sa 2 u 2

a 2 ln(u sa 2 u 2 ) C

yusu2 3 du ysu2 3 du

The ﬁrst integral is evaluated using the substitution t u2 3:

yusu2 3 du 12 yst dt 12 23 t3 2 13 u2 3 3 2

For the second integral we use Formula 21 with a s3 :

ysu2 3 du u su2 3 32 ln(u su2 3 )

Thus

yxsx2 2x 4 dx

13 x2 2x 4 3 2 x 1 sx2 2x 4 32 ln(x 1 sx2 2x 4 ) C

COMPUTER ALGEBRA SYSTEMS

We have seen that the use of tables involves matching the form of the given integrand with the forms of the integrands in the tables. Computers are particularly good at matching patterns. And just as we used substitutions in conjunction with tables, a CAS can perform substitutions that transform a given integral into one that occurs in its stored formulas. So it isn’t surprising that computer algebra systems excel at integration. That doesn’t mean that integration by hand is an obsolete skill. We will see that a hand computation sometimes produces an indeﬁnite integral in a form that is more convenient than a machine answer.

To begin, let’s see what happens when we ask a machine to integrate the relatively simple function y 1 3x 2 . Using the substitution u 3x 2, an easy calculation by hand gives

y 3x 1 2 dx 13 ln 3x 2 C

492 |||| CHAPTER 7 TECHNIQUES OF INTEGRATION

whereas Derive, Mathematica, and Maple all return the answer

13 ln 3x 2

The ﬁrst thing to notice is that computer algebra systems omit the constant of integration. In other words, they produce a particular antiderivative, not the most general one. Therefore, when making use of a machine integration, we might have to add a constant. Second, the absolute value signs are omitted in the machine answer. That is ﬁne if our problem is concerned only with values of x greater than 23 . But if we are interested in other values of x, then we need to insert the absolute value symbol.

In the next example we reconsider the integral of Example 4, but this time we ask a machine for the answer.

EXAMPLE 5 Use a computer algebra system to ﬁnd yxsx2 2x 4 dx.

SOLUTION Maple responds with the answer

31 x2 2x 4 3 2 41 2x 2 s

arcsinh

1 x

x2 2x 4

This looks different from the answer we found in Example 4, but it is equivalent because

the third term can be rewritten using the identity

arcsinh x ln(x s

)

N This is Equation 3.11.3.

x2 1

Thus

arcsinh

x ln 3 1

s|3 1 x

[1 x s

]

1 x 2 3

ln(x 1 s

)

x2 2x 4

The resulting extra term 23 ln(1 s

) can be absorbed into the constant of integration.

Mathematica gives the answer

1 x

arcsinh

3 s

Mathematica combined the ﬁrst two terms of Example 4 (and the Maple result) into a

single term by factoring.

Derive gives the answer

		61 s	x2 2x 4	2x2 x 5 23 ln(s	x2 2x 4	x 1)
The ﬁrst term is like the ﬁrst term in the Mathematica answer, and the second term is
identical to the last term in Example 4.							M
EXAMPLE 6 Use a CAS to evaluate yx x2 5 8 dx.
SOLUTION Maple and Mathematica give the same answer:
	1	x18 25 x16 50x14 17503 x12 4375x10 21875x8 2187503 x6 156250x4 3906252					x2
	18						x2

SECTION 7.6 INTEGRATION USING TABLES AND COMPUTER ALGEBRA SYSTEMS |||| 493

It’s clear that both systems must have expanded x2 5 8 by the Binomial Theorem and then integrated each term.

If we integrate by hand instead, using the substitution u x2 5, we get


N Derive and the TI-89/92 also give this answer.	yx x2 5 8 dx			1	x2 5 9 C
N Derive and the TI-89/92 also give this answer.	yx x2 5 8 dx			18	x2 5 9 C
For most purposes, this is a more convenient form of the answer.								M
EXAMPLE 7 Use a CAS to ﬁnd ysin5x cos2x dx.
SOLUTION	In Example 2 in Section 7.2 we found that
1	ysin5x cos2x dx 31 cos3x 52 cos5x 71 cos7x C
Derive and Maple report the answer
	71 sin4x cos3x	4	sin2x cos3x			8	cos3x
	71 sin4x cos3x	35	sin2x cos3x			105	cos3x

whereas Mathematica produces

645 cos x 1921 cos 3x 3203 cos 5x 4481 cos 7x

We suspect that there are trigonometric identities which show these three answers are equivalent. Indeed, if we ask Derive, Maple, and Mathematica to simplify their expressions using trigonometric identities, they ultimately produce the same form of the answer as in Equation 1. M

7.6E X E R C I S E S

1– 4 Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral.

2x2

dx; entry 33

dx;

entry 55

ysec3 x dx; entry 71

ye2 sin 3 d ;

entry 98

5–30 Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral.

2x cos 1x dx

x2 s

4x2 7

ln(1

)

ytan3 x dx

10.

2y2 3

x2s

4x2 9

11.	y01 t2e t dt
			3
13.	y	tan 1 z					dz
		z 2
15.	ye2x arctan ex dx
	yys								dy
				6 4y 4y2
17.

	ysin2x cos x ln sin x dx
19.

	y	e			x
21.						dx
		3			e2x
23.	ysec5x dx
		s
25.	y		4 ln x 2					dx
					x

12. yx2 csch x3 1 dx

14.ysin 1sx dx

16.yx sin x2 cos 3x2 dx

18.		y	dx
			2x3 3x2
20.		y			sin 2	d

				s
					5 sin
		2

22.		y0		x3s4x2 x4 dx
24.		ysin6 2x dx
		1
	26.	y0		x4e x dx

494 |||| CHAPTER 7 TECHNIQUES OF INTEGRATION

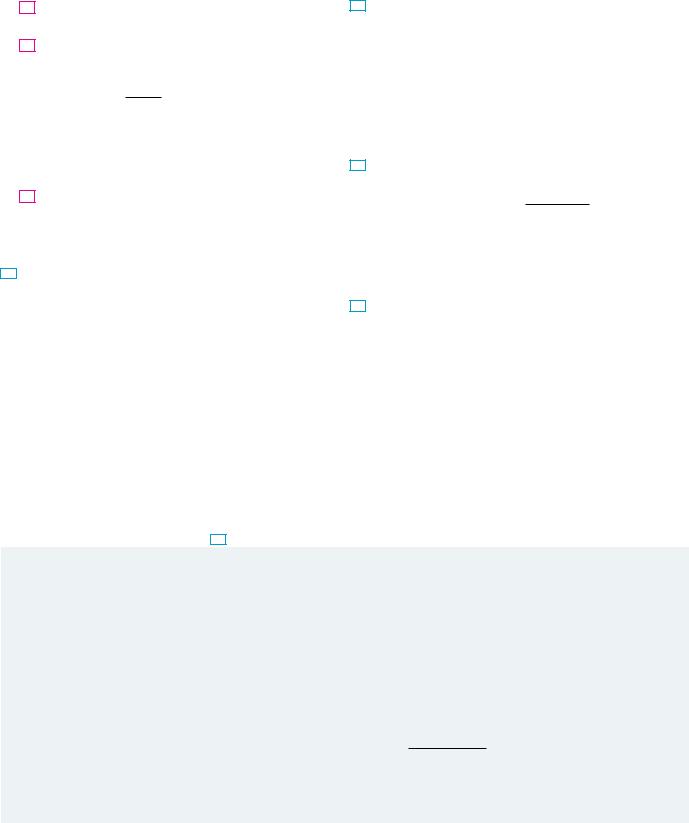
27.

e2x 1

28.

yet sin t 3 dt

sec

tan

29.

x dx

30.

x10 2

9 tan2

31.Find the volume of the solid obtained when the region under the curve y xs4 x2 , 0 x 2, is rotated about the y-axis.

32. The region under the curve y tan2x from 0 to 4 is rotated about the x-axis. Find the volume of the resulting solid.

33.Verify Formula 53 in the Table of Integrals (a) by differentiation and (b) by using the substitution t a bu.

34.Verify Formula 31 (a) by differentiation and (b) by substituting u a sin .

CAS 35– 42 Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent.

35.	ysec4x dx			36.	ycsc5x dx
							dx
37.	yx2sx2 4 dx			38.	y
						ex 3ex 2
39.	yxs		dx	40.	ysin4x dx
		1 2x
41.	ytan5x dx			42.	y		1		dx
						s	1	3

								sx

CAS 43. (a) Use the table of integrals to evaluate F x x f x dx, where

f x		1

	xs1	x2
	xs1	x2

What is the domain of f and F?

(b)Use a CAS to evaluate F x . What is the domain of the function F that the CAS produces? Is there a discrepancy between this domain and the domain of the function F that you found in part (a)?

CAS 44. Computer algebra systems sometimes need a helping hand from human beings. Try to evaluate

y 1 ln x s1 x ln x 2 dx

with a computer algebra system. If it doesn’t return an answer, make a substitution that changes the integral into one that the CAS can evaluate.

CAS 45– 48 Use a CAS to ﬁnd an antiderivative F of f such that F 0 0. Graph f and F and locate approximately the

x-coordinates of the extreme points and inﬂection points of F.

45.	f x		x2 1
		x4 x2 1
46.	f x xe x sin x,			5 x 5
47.	f x sin4x cos6x,			0 x
48.	f x		x3 x
			x6 1

D I S C O V E R Y

CAS

PATTERNS IN INTEGRALS

P R O J E C T

In this project a computer algebra system is used to investigate indeﬁnite integrals of families of

functions. By observing the patterns that occur in the integrals of several members of the family,

you will ﬁrst guess, and then prove, a general formula for the integral of any member of the

family.

(a) Use a computer algebra system to evaluate the following integrals.

(i)

(ii)

x 2 x 3

x 1 x 5

(iii)

(iv)

x 2 x 5

x 2 2

(b) Based on the pattern of your responses in part (a), guess the value of the integral

y x a x b dx

if a b. What if a b?

(c)Check your guess by asking your CAS to evaluate the integral in part (b). Then prove it using partial fractions.

<<< < Предыдущая 39 40 41 42 43 44 45 46 47 48 49 5051 / 9151 52 53 54 55 56 57 58 59 60 61 62 63 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.202055.36 Mб19Calculus, 7th Edition ( PDFDrive.com ).pdf
#
30.12.201945.82 Mб41Complete Solutions Manual for_ SINGLE VARIABLE CALCULUS Early Transcendentals 7th Edition by Stewart ( PDFDrive.com ).pdf
#
30.12.201918.09 Mб36[James_Stewart]_Single_Variable_Calculus_Early_Tr(BookFi).pdf