3.2. Взаимное расположение двух плоскостей

Д ве плоскости в пространстве могут пересекаться, быть параллельными, совпадать. Если плоскости пересекаются, то линией их пересечения будет прямая, и плоскости образуют двугранный угол, который измеряется плоским углом , образованным двумя перпендикулярами, лежащими на гранях угла и имеющими общую вершину. Легко видеть (рис.3.6), что угол  между пересекающимися плоскостями (вид сбоку) равен углу между нормальными векторами этих плоскостей. Пусть даны две плоскости

Нормальные векторы этих плоскостей имеют координаты соответственно , Угол  находится по формуле

(3.5)

Отсюда - условие перпендикулярности двух плоскостей,

- условие параллельности.

Пример 3.2. Найти угол между плоскостями , .

Решение. Выпишем координаты нормальных векторов плоскостей , и найдем угол между ними

следовательно, , то есть плоскости взаимно перпендикулярны.

Уравнение первой степени с п переменными вида называется уравнением гиперплоскости в пространстве Rⁿ. Геометрической интерпретации в Rⁿ (n > 3) оно не имеет.

3.3. Прямая в пространстве r3

П рямую в пространстве можно задать несколькими способами, например, двумя различными точками, двумя пересекающимися плоскостями. Зададим прямую при помощи точки М₀ , через которую она пройдет, и направляющего вектора , который задает направление прямой.

Возьмем на прямой (рис. 3.7)произвольную точку М (x,y,z). Очевидно, что векторы и коллинеарные, то есть , где  - некоторое число (см. формулу (2.1)). Так как , то , откуда, в силу равенства векторов,

или

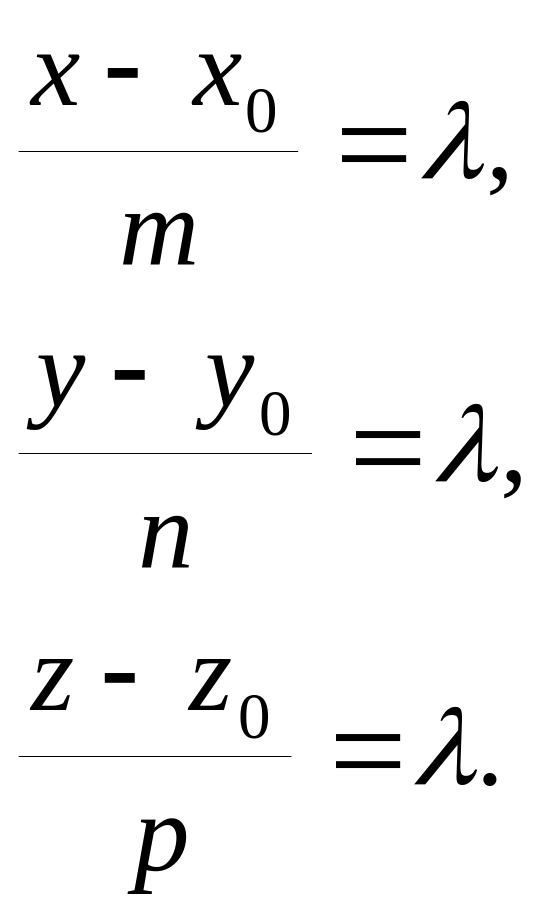
Эти три уравнения называют параметрическими уравнениями прямой, а число – параметром.

Приравнивая левые части, получим:

. (3.6)

Эти уравнения (их два) называются каноническими уравнениями прямой.

Пример 3.4. - канонические уравнения прямой, проходящей через точку М₀(-4; 0; 7) в направлении, определяемом вектором .

Если даны уравнения двух прямых и , лежащих в одной или разных плоскостях, то угол  между ними определяется углом между направляющими векторами и . Таким образом,

(3.7)

Отсюда легко получить условия перпендикулярности и коллинеарности векторов и , а значит и прямых.

Если надо написать уравнение прямой, проходящей через две данные точки и , то в качестве направляющего вектора берется вектор и его координаты представляются вместо m,n,p в (3.6). А вместо подставляются координаты одной из данных точек, например М₁. Тогда получим уравнение

(3.8)

Пример 3.5. найти уравнение прямой, проходящей через точки М₁(0;-4;5), М₂(6;2;-7).

Решение. Пользуясь формулой (3.8) составим уравнение искомой прямой или , или .

3.4. Две важные задачи аналитической геометрии

Задача 1. Найти длину отрезка

Пусть отрезок задан координатами концов: , . Тогда длина отрезка тождественна длине (модулю) вектора . И потому для ее нахождения можно пользоваться формулой (2.14).

Этой же формулой можно пользоваться и в том случае, когда один из концов отрезка не фиксирован, а имеет текущие координаты . В этом случае .

Задача 2. Разделить данный отрезок в заданном отношении. Пусть в R³ дан отрезок прямой (рис. 3.8.), координаты концов которого известны: , . Пусть - делящая точка с переменными координатами и заданное отношение, в котором точка М делит отрезок . Надо найти координаты делящей точки М.

Р ешим задачу в векторном виде. Проведем векторы , соединяющие начало координат О с точками . Рассмотрим векторы и . Они коллинеарны, так как лежат на одной прямой и = по условию (2.1). Но = , = или . Из равенства этих векторов следует пропорциональность соответствующих координат, то есть , , . Из последних трех равенств находим искомые координаты х, у, z делящей точки М:

, , (3.9)

В частности, если точка М делит отрезок пополам, то , =1, и координаты середины отрезка находим по формулам

, , (3.10)

Пример 3.6. Координаты концов отрезка прямой даны: М₁(0; -1; 3), М₂(5; 3; -8). Найти координаты точки М, которая делит данный отрезок в отношении .

Решение. По формулам (3.9) получим

; ;

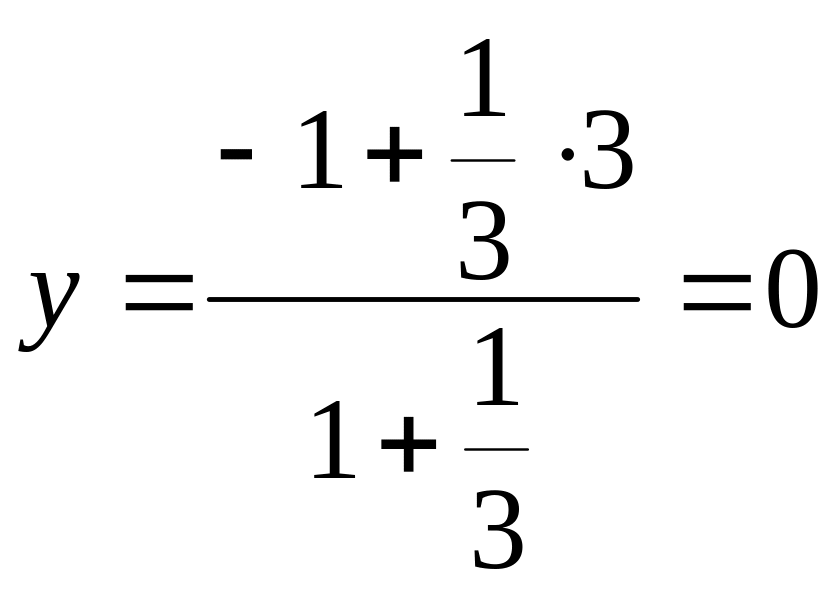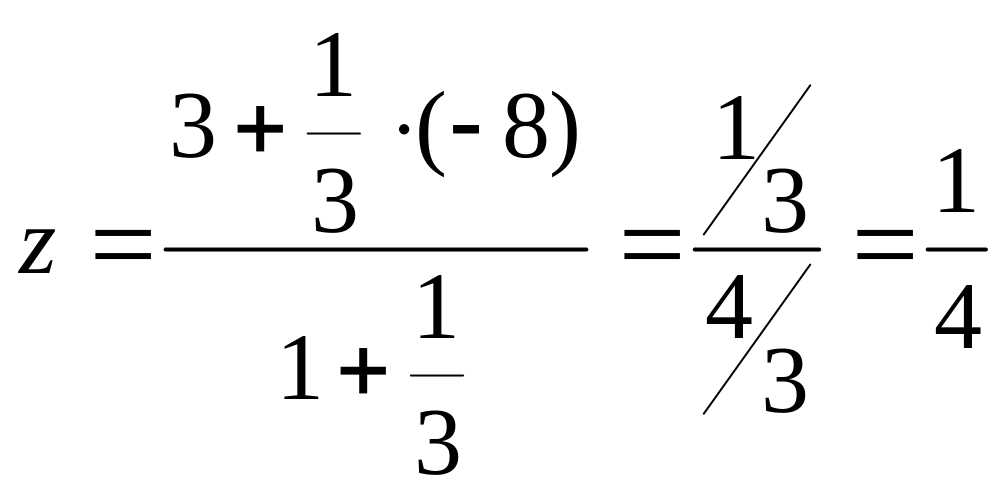
Итак, координаты делящей точки .