4.9.3. Свойств непрерывной на отрезке функции
1. Непрерывная на отрезке [а, b] функция достигает на этом отрезке, по крайней мере один раз наибольшего М и наименьшего т значения.
2. Непрерывная на отрезке [а, b] функция, которая на концах этого отрезка принимает значения разных знаков, хотя бы в одной точке х = с внутри отрезка равна нулю и её график пересекает ось Ох.
3. Непрерывная на отрезке [а, b] функция хотя бы раз принимает любое значение, заключенное между наибольшим М и наименьшим т ее значениями на этом отрезке.
4.10. Некоторые приемы раскрытия неопределенностей вида или при вычислении пределов функции
Приведем примеры раскрытия неопределенностей вида , получаемых при непосредственной подстановке х = а.
1. Разложение на множители и замена предела отношения эквивалентных множителей единицей, которую можно опустить.
а)
.
б)
.
2. В функциях, содержащих радикалы, применяют умножение на сопряженные выражения
в)
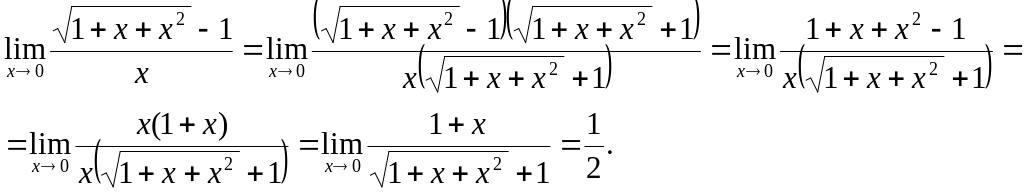
3.
Использование эквивалентности
при
.
Если k
– постоянная, то при
будет и
.
г)
д)
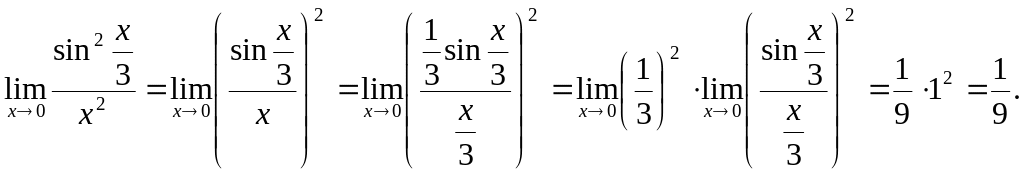
4. Основной прием раскрытия неопределенностей вида , получаемых при нахождении пределов отношения многочленов, если , состоит в почленном делении числителя и знаменателя на самую старшую степень переменной.
е)
,
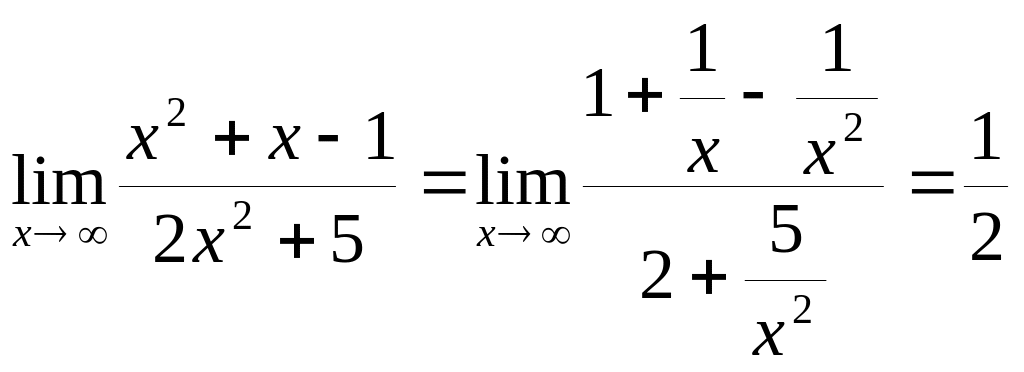пределы дробей
,
,
равны нулю при
как величины, обратные бесконечно
большой величине.
ж)
.
з)
,
как величина, обратная бесконечно малой.
Раскрытие
других видов неопределенностей:
,
,
будут рассмотрены позже.
Лекция 5. Дифференциальное исчисление
5.1. Производная
Понятие производной – основное в дифференциальном исчислении.
Производной
данной функции
называется предел отношения приращения
функции к приращению аргумента, при
условии, что приращение аргумента
стремится к нулю, если предел существует
и конечен.
Обозначения:
;
;
,
.
(5.1)
5.2. Механический смысл производной
П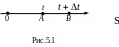
усть
точка движется по прямой вправо от точки
О
(рис. 5.1). Путь S,
пройденный точкой за время t,
является функцией времени, то есть
.
Зная закон движения можно определить
среднюю скорость движения за любой
промежуток времени. Пусть в момент
времени t
движущаяся точка находилась в положении
А, а в момент времени
- в положении В. За время
точка прошла путь
.
Средняя скорость движения за промежуток
времени
будет
.
Если движение равномерное, то средняя скорость постоянна. Если же движение неравномерное, то средняя скорость на разных участках разная.
Очевидно,
что средняя скорость тем точнее, чем
меньше промежуток времени
.
Поэтому вводится понятие мгновенной
скорости прямолинейного движения или
скорости в данный момент времени
.
Ею называется предел средней скорости
при
:
(5.2)
Таким образом, мгновенная скорость это производная от закона движения по времени. Она зависит от выбранного момента времени t и поэтому является функцией от t. Мгновенную скорость ввел И. Ньютон (1642 – 1727) – великий английский математик, физик и астроном, занимаясь задачей описания движений.
Итак, механический смысл производной – мгновенная скорость. Оказалось, что это понятие можно обобщить на скорости других процессов: скорость химической реакции, скорость роста биомассы, скорость прироста денежного вклада и т.д.