1.4. Системы линейных уравнений

Напомним, что системой называют конечное множество уравнений, а решением ее – упорядоченную систему чисел, являющуюся решением каждого из уравнений.

Система линейных уравнений с неизвестными (линейная система) имеет вид:

(1.10)

где и – числа, называемые соответственно коэффициентами и свободными членами системы линейных уравнений.

Система совместна, если она имеет хотя бы одно решение и несовместна, если она не имеет решений.

Совместная система – определенная, если решение единственно и неопределенная, если их более одного.

Рассмотрим некоторые способы решения линейных систем.

1.4.1. Метод Крамера

Использование его возможно, если число уравнений и число неизвестных в (1.10) совпадают, т.е. .

Если определитель D системы (1.10), составленный из коэффициентов а₁₁,а₁₂,…,а_nn, при неизвестных х₁, х₂, …,х_n, не равен нулю, то система совместна и имеет единственное решение, которое можно найти по формулам Крамера:

, , …, (1.11)

где D₁, D₂, ..., D_n, - определители n-го порядка, которые получаются из определителя D системы, если в нем заменить соответственно первый, второй и т.д., n-й столбец коэффициентов при x₁, x₂, ..., х_n, столбцом свободных членов. Если же D = 0, то система либо несовместна, либо неопределенна.

Пример 1.11. Решить методом Крамера систему уравнений

Решение: Определитель системы не равен нулю, значит, система совместна.

Найдем определители D₁, и D₂ и вычислим неизвестные по формулам (1.11).

Проверка подстановкой показывает, что x₁ = 6, х₂= -1 действительно являются решением системы.

1.4.2. Метод обратной матрицы

Вернемся к традиционной записи системы (1.10) и «сконструируем» три матрицы:

, ,

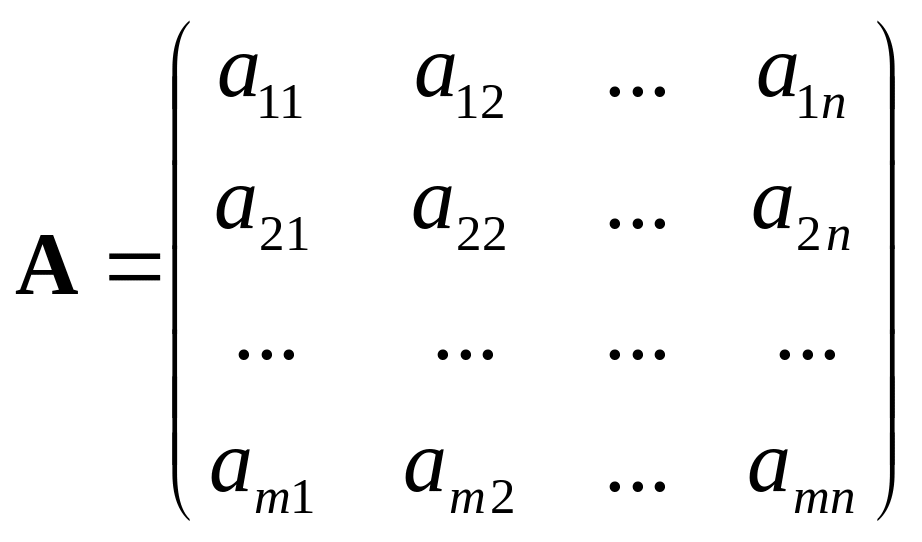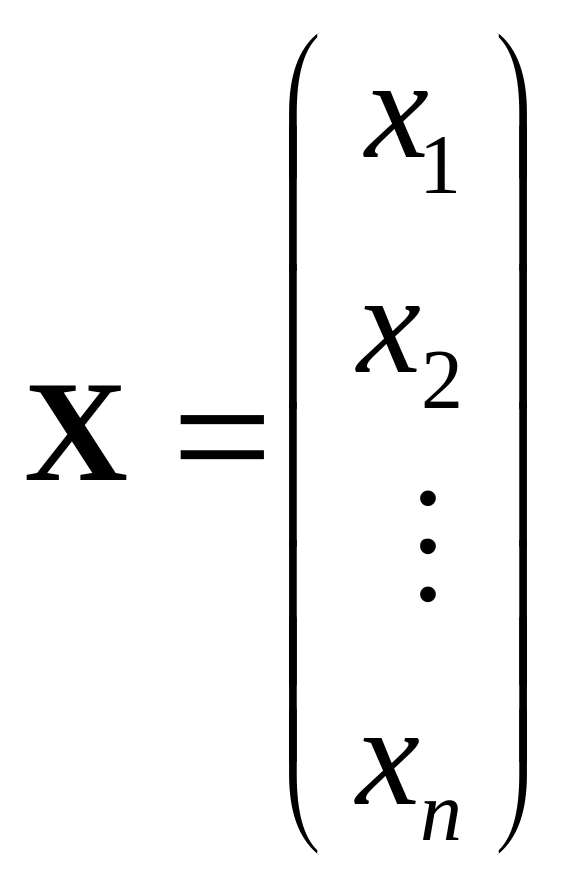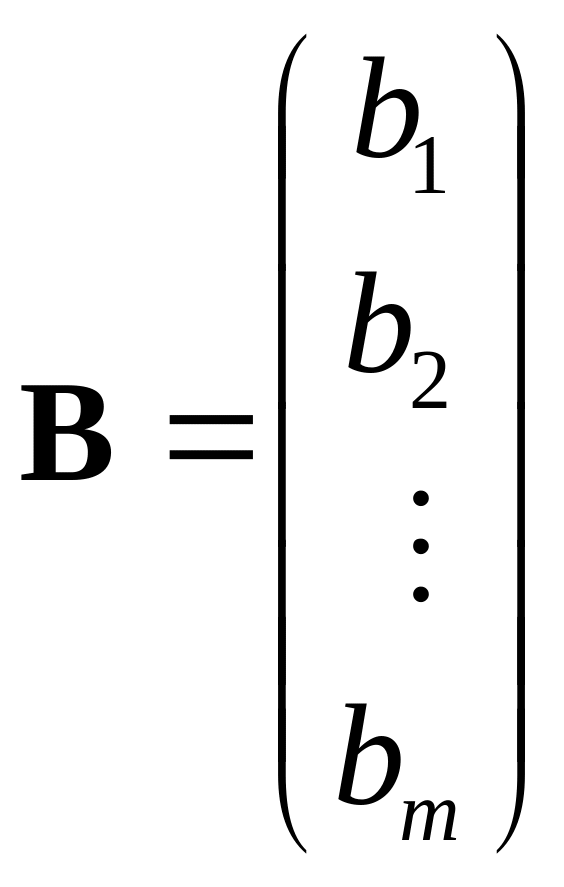
матрицу системы А (ее элементы – коэффициенты при неизвестных системы уравнений), матрицу – столбец неизвестных X и матрицу столбец свободных членов В.

Зная правило умножения матриц, легко убедиться в том, что выражение

(1.12)

есть не что иное, как запись системы линейных уравнений в матричной форме.

Полагая, что число уравнений и число неизвестных совпадают ( ) и матрица А – не вырожденная ( ), умножим обе части (1.12) на матрицу слева. . Зная уже, что , а получим

(1.13)

Пример 1.12 Решить линейную систему методом обратной матрицы.

; ; ;

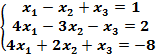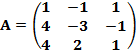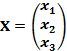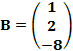
Используя свойства определителя вычислим

.

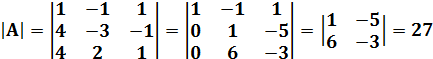и матрица А – не вырожденная.

Составим матрицу , для чего вычислим алгебраические дополнения элементов матрицы А.

; ; ;

; ; ;

; ; ;

Получим: 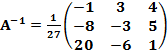и найдем =

;

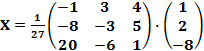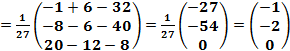Проверка подстановкой подтверждает – решение верно.

1.4.3. Метод Гаусса

Рассмотрим решение системы (1.10) m линейных уравнений с n неизвестными (m  n). Метод Гаусса (К.Ф. Гаусс, 1777-1855, немецкий математик) - это метод последовательного исключения неизвестных, реализуемый в матричной форме. Он состоит в том, что с помощью элементарных преобразований система уравнений приводится к равносильной (эквивалентной) системе треугольного или ступенчатого вида, где в каждом следующем уравнении на одно неизвестное меньше, чем в предыдущем.

Последовательные исключения неизвестных называют прямым ходом метода Гаусса.

Если m = n и число уравнений в процессе исключений не изменилось, то из последнего уравнения находят x_n и подставляют в предпоследнее уравнение, откуда находят x_n-1, и так далее до х₁. Такой процесс вычисления неизвестных называют обратным ходом метода Гаусса. Если и после приведения системы к ступенчатому виду в ней осталось m уравнений, то члены с неизвестными х_т+1 , х_m+2 , ..., х_n, переводят в правые части уравнений и полагают эти неизвестные свободными, а неизвестные x₁, х₂ ,..., х_m - базисными. Обратным ходом метода Гаусса находят базисные неизвестные, выраженные через свободные.

К эквивалентным преобразованиям системы относятся:

1. перестановка уравнений в системе;

2. перестановка слагаемых в уравнении;

3. умножение обеих частей уравнения на одно и то же число;

4. сложение любого уравнения с любым другим уравнением данной системы

Преобразования удобно проводить не с самими уравнениями, а с расширенной матрицей системы, составленной из коэффициентов при неизвестных и свободных членов. (Теорема Кронекера-Капелли: для того, чтобы система была совместна, необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы системы). Обращение элементов основной матрицы системы в нули означает исключение соответствующих неизвестных.

Если в процессе исключений получатся строки, состоящие только из нулей, их вычеркивают. Это значит, что каждое из вычеркнутых уравнений системы является линейной комбинацией других уравнений, а соответствующая строка матрицы – линейной комбинацией других строк.

Если в какой-нибудь строке расширенной матрицы системы слева от вертикальной черты, отделяющей столбец свободных членов, окажутся все элементы, равные нулю, а справа элемент не равный нулю, решение системы прекращают, она несовместна.

Треугольная матрица, полученная в ходе исключения неизвестных, содержит ниже (выше) главной диагонали все элементы нулевые, а на главной диагонали - ненулевые. Ее определитель равен произведению элементов этой диагонали и отличен от нуля. Количество элементов главной диагонали равно рангу матрицы - максимальному числу линейно независимых уравнений системы.

Пример1.13. Решить методом Гаусса систему уравнений

Решение: Выпишем расширенную матрицу системы, записав коэффициенты второго уравнения в первую ее строку, так как коэффициент при х₁ равен 1, а это удобно для исключений неизвестных.

1-й шаг 2-й шаг 3-й шаг

  

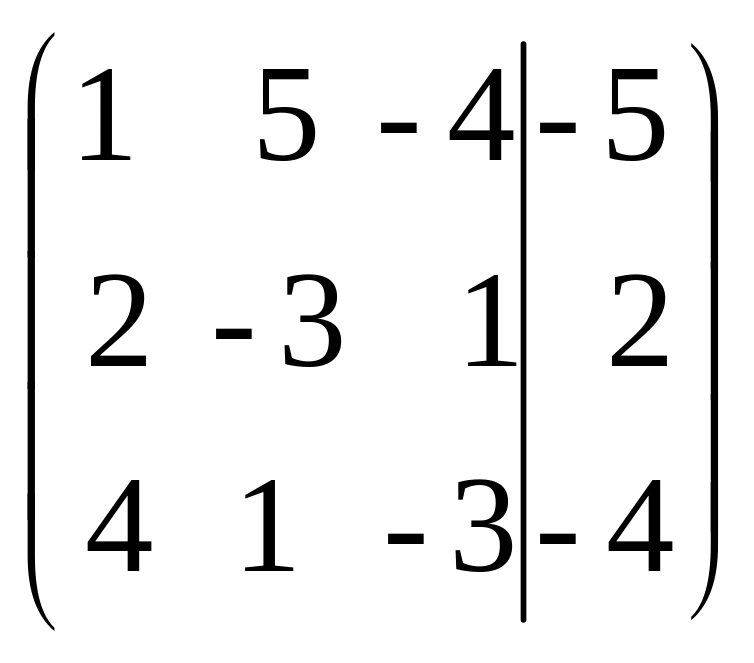
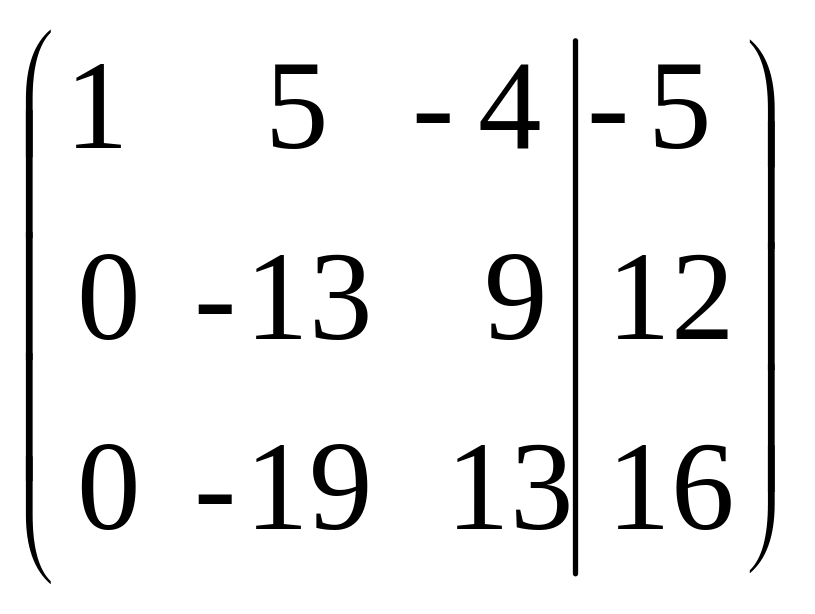
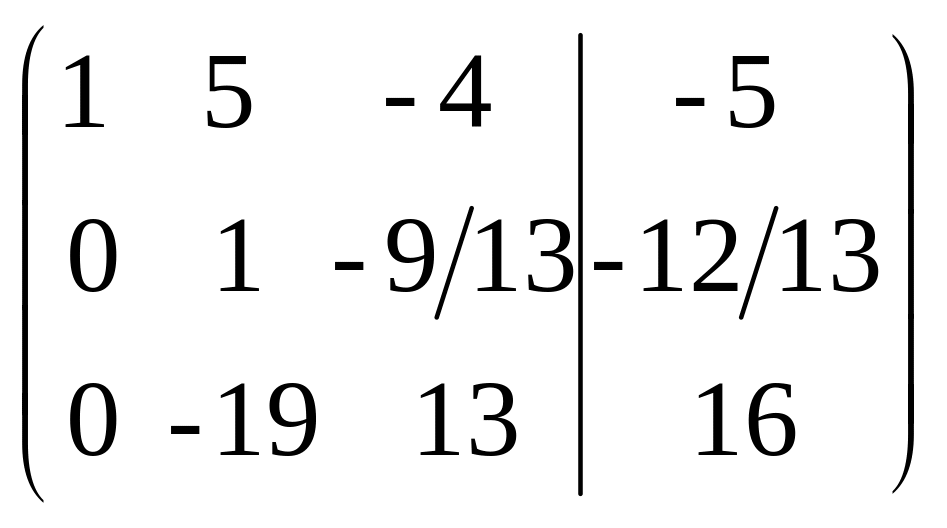
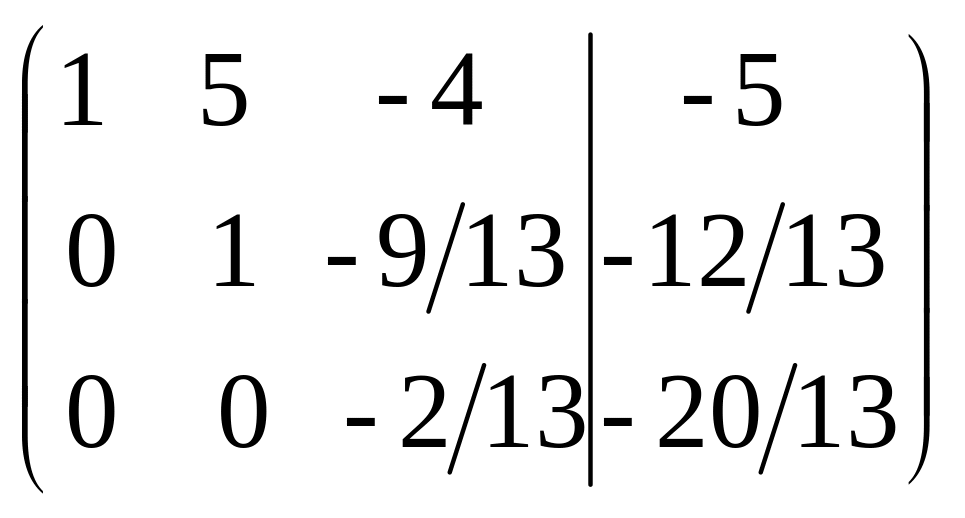
Пояснение:	1-й шаг.	Первую строку, в которой первый элемент 1  0, приняли за разрешающую и записали без изменения. Элементы первой строки умножили на -2 и сложили с соответствующими элементами второй строки. Затем элементы первой строки умножили на -4 и сложили с элементами третей строки.
	2-й шаг.	Первую и третью строки записали без изменения, а вторую почленно разделили на -13 и приняли ее за разрешающую.
	3-й шаг.	Первую и вторую строки записали без изменения. Элементы второй строки умножили на 19 и сложили с элементами третей строки.

Слева от вертикальной черты получили треугольную матрицу. Возвращаясь к системе и идя обратным ходом метода Гаусса, получили уравнение -2/13 х₃ = -20/13, откуда х₃ = 10. Подставляя х₃ = 10 во второе уравнение системы, получим х₂ = -12/13+ 9/1310 = 6. Из первого уравнения будем иметь x₁ =-5-56+410=10. Итак, x₁ =5, х₂ =6, x₃ =10 - решение системы. Проверка подтверждает его правильность.