3.6. Угол между двумя прямыми на плоскости

Если прямые заданы общими уравнениями и , то угол между ними такой же, как угол между нормальными векторами и прямых и находится по формуле, аналогичной формуле (3.5)

(3.18)

условие перпендикулярности прямых (3.19)

условие параллельности прямых (3.20)

Если прямые заданы уравнениями с угловым коэффициентом и , то угол между ними можно найти по формуле

(3.21)

условие перпендикулярности ,

условие параллельности .

Если речь идет об угле между двумя прямыми и не указан порядок, в котором они рассматриваются, то можно устанавливать этот порядок произвольно. Очевидно, что изменение порядка повлечет за собой изменение знака тангенса угла.

Пример 3.6. Найти угол между прямыми и .

Решение I. Выпишем нормальные векторы данных прямых и . Пользуясь формулой (3.16), получим

 = 7444.

Решение II. Запишем уравнение прямых в форме . Получим , . Из этих уравнений видно, что , . Пользуясь формулой (3.21), получим

,

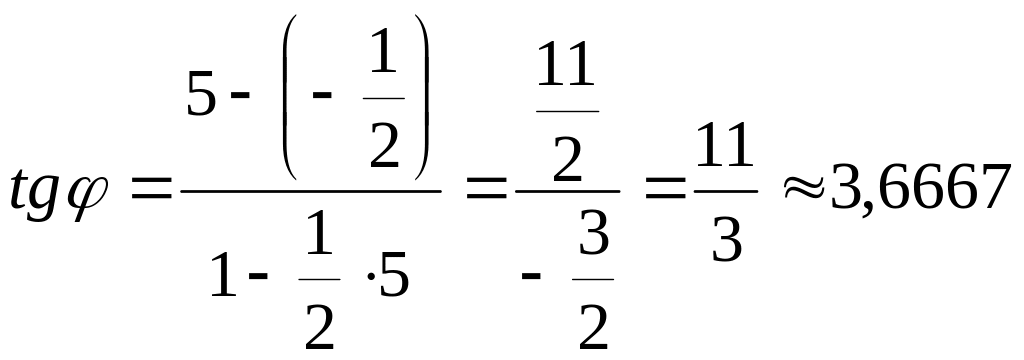 = 7444.

Для нахождения расстояния от данной точки до данной прямой удобно пользоваться формулой

, (3.22)

3.7. Площадь треугольника

Треугольник – одна из самых распространенных фигур и надо уметь вычислять площадь треугольника средствами аналитической геометрии.

Пусть даны вершины треугольника А(х₁, у₁), В(х₂, у₂), С(х₃,у₃). Надо найти формулу, которая бы выражала площадь S треугольника АВС через координаты его вершин.

О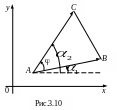 бозначим стороны АВ и АС треугольника как векторы, имеющие общее начало в точке А и следующие координаты , . Пусть угол между вектором и осью Ох равен , угол между вектором и осью Ох равен , а угол между самими векторами и равен  (рис. 3.10).

Из элементарной геометрии известно, что площадь S треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними: . Если воспользуемся формулой синуса разности двух углов и определением проекции вектора на ось (2.2), то получим

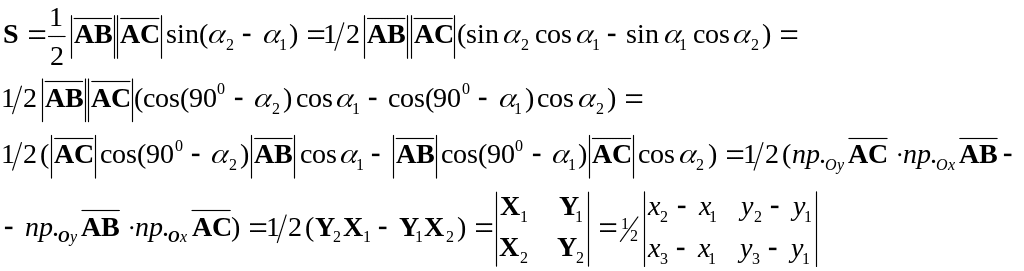
Этот определитель может оказаться как положительным, так и отрицательным (если > ), поэтому (3.23)

Итак, в 3-й лекции мы познакомились с некоторыми важными понятиями аналитической геометрии. В основе последней лежит метод координат, введенный в науку французским математиком и философом Р. Декартом, а главная ее идея заключается в возможности представлять геометрические объекты в виде алгебраических уравнений и переводить геометрические задачи на язык алгебры.

Лекция 4. Введение в анализ

Обратимся теперь к математике непрерывных величин. Величиною будем называть все то, что может быть выражено числом. Будем рассматривать величины, которые выражаются только действительными числами: натуральными, целыми, рациональными, иррациональными.

Величины могут быть постоянными и переменными. Среди постоянных будем различать абсолютные постоянные, например, отношение длины окружности к ее диаметру (число ); отношение диагонали квадрата к его стороне ( ) и другие, и постоянные в условиях данной задачи, например, высота данной пирамиды равна 30 см; площадь данной трапеции равна 24 кв. см и тому подобное. Обозначать постоянные величины будем большими и малыми начальными буквами латинского алфавита: А, В, С, …, а, b, с, …

Переменная величина – величина, которая принимает различные числовые значения. Например, температура воздуха в каждой точке пространства меняется в течение суток, проходя бесконечное множество значений от наименьшего до наибольшего. Переменные величины будем обозначать конечными буквами латинского алфавита X, Y, Z, … , х, у, z, …