
- •Кафедра физики и высшей математики
- •Часть I
- •Лекция 1. Определители и матрицы
- •1.1. Матрицы: основные сведения
- •1.2. Определители: их вычисление и свойства
- •Определители второго порядка вычисляют по формуле
- •1.3. Действия над матрицами. Обратная матрица. Ранг матрицы
- •1.4. Системы линейных уравнений
- •1.4.1. Метод Крамера
- •1.4.2. Метод обратной матрицы
- •1.4.3. Метод Гаусса
- •Лекция 2. Векторы
- •2.1. Геометрические векторы
- •2.2. Линейные операции над векторами
- •2.3. Проекция вектора на ось
- •2.4. Разложение вектора по осям координат
- •2.5. Линейные операции над векторами, заданными в координатной форме
- •2.6. Скалярное произведение двух векторов
- •2.8. Алгебраический подход к понятию n-мерного вектора
- •2.9. Линейная зависимость векторов
- •Лекция 3. Плоскость и прямая
- •3.1. Плоскость в пространстве
- •3.2. Взаимное расположение двух плоскостей
- •3.3. Прямая в пространстве r3
- •3.4. Две важные задачи аналитической геометрии
- •3.5. Прямая на плоскости
- •Если а 0, в 0, с 0, то прямая (3.11) пересекает обе координатные оси.
- •Раскрывая скобки в уравнении (3.15), получим
- •3.6. Угол между двумя прямыми на плоскости
- •3.7. Площадь треугольника
- •Лекция 4. Введение в анализ
- •4.1. Функция
- •4.2. Предел
- •4.3. Предел переменной величины
- •4.4. Предел функции
- •4.5. Бесконечно малые и их основные свойства
- •4.6. Основные теоремы о действиях с пределами
- •4.7. Сравнение бесконечно малых
- •4.8. Два замечательных предела
- •4.9. Непрерывность функции
- •4.9.1. Приращение аргумента и приращение функции
- •4.9.2. Непрерывность функции в точке
- •4.9.3. Свойств непрерывной на отрезке функции
- •4.10. Некоторые приемы раскрытия неопределенностей вида или при вычислении пределов функции
- •Лекция 5. Дифференциальное исчисление
- •5.1. Производная
- •5.2. Механический смысл производной
- •5.3. Геометрический смысл производной
- •5.4. Дифференцируемость и непрерывность функции
- •5.5. Схема нахождения производной
- •5.6. Таблица производных основных элементарных функций
- •5.7. Правила дифференцирования элементарных функций
- •5.8. Производная сложной функции
- •5.9. Производная параметрически заданной функции
- •5.10. Неявная функция и ее дифференцирование
- •5.11. Дифференциал
- •5.12. Производные и дифференциалы высших порядков
- •5.13. Частные производные
- •5.14. Полный дифференциал
- •Лекция 6. Приложения производной к исследованию функций
- •6.1. Правило Лопиталя
- •6.2. Экстремум функции
- •6.2.1. Возрастание и убывание функции, его аналитические признаки
- •6.2.2. Точка максимума и минимума
- •6.2.3. Необходимое условие экстремума
- •6.2.4. Достаточные признаки существования экстремума
- •6.3. Признаки выпуклости и вогнутости графика функции. Точки перегиба
- •6.3.1. Необходимые и достаточные признаки выпуклости и вогнутости графика
- •6.4. Второй достаточный признак экстремума
- •6.5. Асимптоты
- •6.6. Схема общего исследования функции и построения ее графика
- •Лекции для студентов высших учебных заведений, обучающихся заочно по экономическим специальностям. Часть I
2.8. Алгебраический подход к понятию n-мерного вектора
n-мерным
вектором называется упорядоченный
набор из n
действительных чисел, записанный в виде
строки или столбца. Обозначение:
![]() где
где
![]() …
-
элементы
или координаты вектора х.
Число координат определяет размерность
вектора.
Векторы равны между собой только в том
случае, когда у них одинаковая размерность
и равны соответствующие координаты.
Отсюда следует, что координаты вектора
нельзя менять местами, так как в результате
получатся неравные векторы.
…
-
элементы
или координаты вектора х.
Число координат определяет размерность
вектора.
Векторы равны между собой только в том
случае, когда у них одинаковая размерность
и равны соответствующие координаты.
Отсюда следует, что координаты вектора
нельзя менять местами, так как в результате
получатся неравные векторы.
Над n-мерными векторами можно выполнять линейные операции: складывать, вычитать, умножать на число по известным уже нам правилам для трехмерных векторов, заданных в координатной форме.
Скалярным
произведением двух n-мерных
векторов
![]() и
и
![]() называется число
называется число
![]() .
(2.16)
.
(2.16)
В экономических задачах можно рассматривать скалярное произведение вектора цен х на вектор объема продукции у. Скалярное произведение ху в этом случае дает суммарную стоимость продукции.
Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Нетрудно проверить, что линейные операции над n-мерными векторами х,у,z удовлетворяют следующим условиям:
х + у = у + х

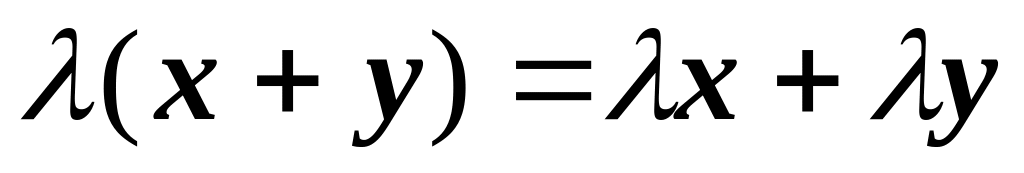
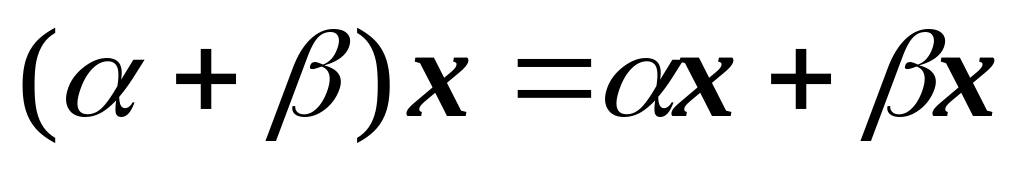
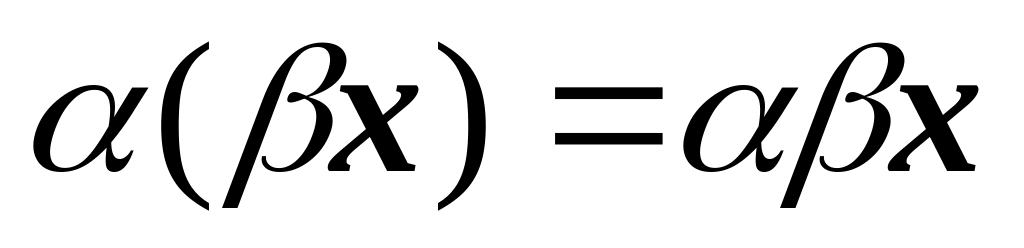
5)
![]() ,
где
,
где
![]() - некоторые числа.
- некоторые числа.
Скалярное произведение n-мерных векторов обладает следующими свойствами:
1)
![]() ,
причем хх
= 0 только при х
= 0
,
причем хх
= 0 только при х
= 0
2) ху = ху
3)
![]()
4)
![]()
Множество n-мерных векторов образует линейное n-мерное пространство, обозначаемое Rn, так как для любых двух векторов выполняются операции сложения и умножения на число, причем эти операции удовлетворяют условиям 1) - 6). В частности, пространства трехмерных и двухмерных векторов обозначаются R3 и R2 .
2.9. Линейная зависимость векторов
Линейной
комбинацией векторов
![]() называется сумма произведений этих
векторов на действительные числа
называется сумма произведений этих
векторов на действительные числа
![]() ,то
есть сумма
,то
есть сумма
![]() (2.17)
(2.17)
которая тоже является вектором. Числа называются коэффициентами линейной комбинации.
Пример
2.2.
Составить линейную комбинацию векторов
![]() =
(3; -2; 4) и
=
(3; -2; 4) и
![]() =(1;
-1; -5) с коэффициентами
=(1;
-1; -5) с коэффициентами
![]() = 2,
= 2,
![]() =
-3 .
=
-3 .
Решение. Вычислим сначала 2 и -3
2 = 2(3; -2; 4) = (6; -4; 8); -3 = -3(1; -1; -5) = (-3; 3; 15).
Теперь составим линейную комбинацию
2 - 3 =(6; -4; 8)+ (-3; 3; 15)=(3; -1; 23)
Пример
2.3.
Составить линейную комбинацию векторов
=(5;
4),
=(-1;
2),
![]() =(-10;
-1) с коэффициентами
= 3,
=
-5,
=(-10;
-1) с коэффициентами
= 3,
=
-5,
![]() =
2.
=
2.
Решение. Находим искомую линейную комбинацию:
3
- 5
+
2
=
3(5; 4)- 5(-1; 2)+ 2(-10; -1) = (15; 12)+(5; -10)+(-20; -2) = (0;
0)=![]()
Этот пример показывает, что в некоторых случаях можно подобрать коэффициенты так, что линейная комбинация системы векторов окажется равной нуль-вектору.
Система
векторов называется линейно
зависимой, если
из этих векторов можно составить нулевую
линейную комбинацию
![]() =
,
причем хотя бы один из коэффициентов
не
равен нулю.
=
,
причем хотя бы один из коэффициентов
не
равен нулю.
Если из системы векторов нельзя составить нулевую линейную комбинацию, то система векторов называется линейно независимой.
Если система векторов линейно зависима, то хотя бы один из них можно представить виде линейной комбинации остальных векторов. На плоскости можно найти линейно независимую систему из двух, но не большего числа векторов, в трехмерном пространстве - из трех, но не большего числа векторов и так далее.
Векторное
пространство называется n-мерным,
если в нем существует в точности n
линейно независимых векторов. Базисом
n-мерного
пространства называется любая система
из n
линейно независимых векторов этого
пространства. Базис в векторном
пространстве играет роль, сходную с
ролью системы координат. Каждый вектор
пространства можно выразить через
векторы базиса. Смотрите, например,
представление трехмерного вектора в
компонентах (2.4), где
![]() -
базисные
векторы.
-
базисные
векторы.
