Лекция 6. Приложения производной к исследованию функций

Одним из важнейших приложений дифференциального исчисления является разработка общих методов исследования функции.

Производная используется также при решении экстремальных задач, которые сводятся к нахождению наибольших или наименьших значений функции в области её определения. Такие задачи возникают в различных областях знаний, в том числе в экономике. В каждой конкретной задаче, прежде чем приступить к её решению, надо выяснить существует ли наибольшее или наименьшее значение рассматриваемой функции. Ответ на этот вопрос даёт теорема К. Вейерштрасса: непрерывная на отрезке функция ограничена и достигает хотя бы раз своего наибольшего или наименьшего значений. На эту теорему опирается ряд других теорем, которые служат теоретической основой многих приложений производной.

6.1. Правило Лопиталя

Французский математик Г.Лопиталь первый опубликовал правило раскрытия неопределённостей вида или , возникающих при вычислении пределов. Другие неопределённости , при помощи алгебраических преобразований сводятся к неопределённостям вида или .

Правило Лопиталя: Для неопределённостей вида или предел отношения двух функций равен пределу отношения их производных, если функции эти непрерывны в окрестности соответствующей точки за исключением самой этой точки (в проколотой окрестности точки).

(6.1)

Правило Лопиталя можно применять повторно.

Пример 6.1. а)

б)

в) .

Здесь в первом примере имеем дважды неопределённость , во втором – один раз неопределённость вида , а в третьем трижды имеем неопределённость вида .

6.2. Экстремум функции

6.2.1. Возрастание и убывание функции, его аналитические признаки

Большинство функций на разных промежутках области определения ведут себя по-разному, на одних возрастают, на других убывают. Поэтому мы будем дальше рассматривать поведение функции на отрезке .

Если для любых двух точек х₁ и х₂ из интервала (а, b) большему значению аргумента соответствует большее значение функции, то есть для х₂>х₁ будет f(x₂)>f(x₁), то функция у=f(x) называется возрастающей на (а, b); если для х₂>х₁ будет f(x₂)<f(x₁), то функция называется убывающей на (а, b).

Функция, которая на интервале только возрастает или только убывает, называется монотонной.

Узнать, является ли функция возрастающей или убывающей можно используя следующие теоремы.

Т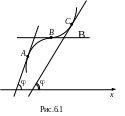 еорема 1. Если функция у=f(x) дифференцируема на (а, b) и возрастает, то её первая производная неотрицательна во всех точках этого интервала, то есть на (а, b).

Теорема 2. Если функция у=f(x) убывает на (а, b), то , т.е. неположительная на (а, b). Эти теоремы определяют необходимые признаки возрастания и убывания функции на интервале.

Для обоснования этих теорем сошлёмся на геометрический смысл производной. Производная функции у=f(x) равна угловому коэффициенту касательной к графику функции в каждой её точке, где производная существует. Легко видеть (рис.6.1.), что если функция возрастает, то угол наклона касательной острый (в точках А, С) или, в крайнем случае, равен нулю (в точке В), но тангенс острого угла положительный, а нулевой – равен нулю. Таким образом, для возрастающей на (а, b) функции

А налогично, если функция дифференцируема на (а, b) и убывает, то углы наклона касательных тупые (или равны нулю) (рис. 6.2.). Но тангенсы тупых углов отрицательны, а нулевых – равны нулю. Следовательно,

Обратные теоремы определяют достаточные признаки возрастания и убывания функции.

Теорема 3. Если на (а, b), то функция у=f(x) возрастает на (а,b).

Теорема 4. Если на (а, b), то функция у=f(x) убывает на (а, b).

В самом деле, если на (а, b) , то угловой коэффициент касательной в каждой точке (а, b) положительный, а значит угол её наклона острый. Но это возможно только, если кривая возрастает. Аналогично, если , то угол наклона касательной в каждой точке (а, b) тупой. А это возможно только, если функция убывает.