6.2.2. Точка максимума и минимума

Точка х=х₁ называется точкой максимума функции у=f(x), если для всех точек некоторого интервала, содержащего точку х₁, будет выполняться равенство при любых достаточно малых или .

Точка х=х₂ называется точкой минимума функции у=f(x), если для всех точек некоторого интервала, содержащего точку х₂, будет выполняться неравенство , где или .

Точка максимума и минимума называются точками экстремума функции. Рассмотрим методы нахождения экстремумов.

6.2.3. Необходимое условие экстремума

Теорема. Если дифференцируемая функция у=f(x) имеет в точке х=х₀ экстремум, то её производная в точке обращается в нуль, то есть , или не существует.

Пусть для определённости точка х₀ является точкой максимума. Тогда из определения максимума следует, что или . Составим и оценим знаки отношения приращений , а именно: , если и , если .

По условию теоремы функция дифференцируема в точке х₀, значит существует предел , и он не зависит от того, как стремится к нулю. Беря пределы от обеих приведённых выше неравенств, получаем с одной стороны , если >0, с другой , если <0. но так как есть определённое число, то два последних неравенства совместимы, только если .

Аналогичным образом теорема доказывается для случая, когда х₀ – точка минимума.

Точки, в которых производная обращается в нуль или не существует, называются критическими точками первого рода или точками подозрительными на экстремум. Условия существования критических точек, в которых производная равна нулю, описываются условием теоремы Ролля, которую мы приведём без доказательств. Если функция у=f(x) непрерывна на отрезке и дифференцируема в каждой его точке, а не на концах отрезка имеем значения f(a)=f(b), то внутри отрезка найдётся хотя бы одна точка х=с, в которой производная данной функции равна нулю, то есть .

Геометрически это значит, что найдётся хотя бы одна точка a<c<b, в которой касательная параллельна оси Ох.

Для того, чтобы найти точку экстремума функции у=f(x) необходимо найти её производную, приравнять её нулю и решить полученное уравнение. Корни этого уравнения, а также точки разрыва производной будут критическими точками.

Пример 6.1. Найти критические точки функции у=2х³-6х²+1.

Р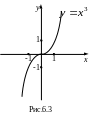 ешение. Найдём производную . Решим уравнение 6х²-12х=0, его корни х₁=0, х₂=2 – критические точки.

Пример 6.2. Найти критические точки функции у=х³.

Решение. - критическая точка.

Легко увидеть (рис.6.3.), что х=0 для функции у=х³ не является точкой экстремума. Так что имеющееся условие экстремума (или ) является лишь необходимым, но недостаточным.

6.2.4. Достаточные признаки существования экстремума

Первый достаточный признак экстремума формулируется на основе изменения знака первой производной при переходе через критическую точку. О втором признаке экстремума речь пойдёт ниже в § 6.4.

Теорема (первый признак экстремума): Если х₀ – критическая точка функции у=f(x) и в некоторой окрестности точки х₀, переходя через неё слева направо, производная меняет знак на противоположный, то х₀ является точкой экстремума. Причём, если знак производной меняется с «+» на «-», то х₀ – точка максимума, а f(x₀) – максимум функции, а если производная меняет знак с «-» на «+», то х₀ – точка минимума, а f(x₀) – минимум функции.

Рассмотренный экстремум носит локальный (местный) характер и касается некоторой малой окрестности критической точки.

Точки экстремума и точки разрыва делят область определения функции на интервалы монотонности.

Пример 6.3. В примере 6.1. мы нашли критические точки х₁=0 и х₂=2.

Выясним, действительно ли в этих точках функция у=2х³-6х²+1 имеет экстремум. Подставим в её производную значения х, взятые слева и справа от точки х₁=0 в достаточно близкой окрестности, например, х=-1и х=1. получим . Так как производная меняет знак с «+» на «-», то х₁=0 – точка максимума, а максимум функции . Теперь возьмем два значения х=1 и х=3 из окрестности другой критической точки х₂=2. Уже показано, что , а . Так как производная меняет знак с «-» на «+», то х₂=2 – точка минимума. А минимум функции .

Чтобы найти наибольшее и наименьшее значение функции непрерывной на отрезке нужно вычислить её значение во всех критических точках и на концах отрезка, а затем выбрать из них наибольшее и наименьшее.