5.3. Геометрический смысл производной

В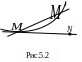 едем понятие касательной к произвольной кривой. Касательной к кривой в точке М называют ту прямую MN, с которой стремится совпасть секущая , когда точка неограниченно приближается вдоль кривой к точке (рис. 5.2). Касательная к кривой в точке может и пересекаться с этой кривой при своем продолжении.

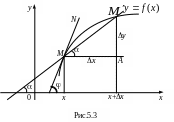
Пусть дан график некоторой функции . Пусть - некоторая фиксированная точка на этом графике (рис. 5.3). Проведем через эту точку секущую и прямую , параллельную оси Ох, а также ординаты точек и . Из прямоугольного треугольника имеем . Но , тогда . Если перейти к пределу при , то точка и секущая , то есть секущая стремится к положению касательной в точке . При этом , а . Таким образом вместо равенства получим равенство

(5.2)

Итак, производная в фиксированной точке численно равна угловому коэффициенту касательной к кривой в этой точке. В этом и заключается геометрический смысл производной.

5.4. Дифференцируемость и непрерывность функции

Нахождение производной называется дифференцированием (от латинского differentia – разность, вспомним, что и - разности). Функция имеющая производную, называется дифференцируемой.

Теорема. Если функция дифференцируема в некоторой точке , то она непрерывна в этой точке.

Пусть функция имеет производную в точке , то есть

,

тогда, по определению предела переменной (теорема 2, §3.5),

,

где  - бесконечно малая. Но тогда

Отсюда видно, что при будет , а это и есть условие непрерывности функции в точке. Мы получили этот результат, допустив, что функция имеет производную, то есть дифференцируема.

Следствие: В точках разрыва функция не может иметь производную.

У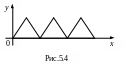 тверждение, обратное этой теореме, неверно. Из того, что в некоторой точке функция непрерывна, еще не следует, что она дифференцируема в этой точке. Например, непрерывная функция, график которой изображен на рисунке 5.4 не является дифференцируемой в «углах» ломаной, так как положение касательной в точках излома неопределенное.

5.5. Схема нахождения производной

Для нахождения производной функции необходимо произвести следующие действия (четырехшаговая схема):

1. записать ;

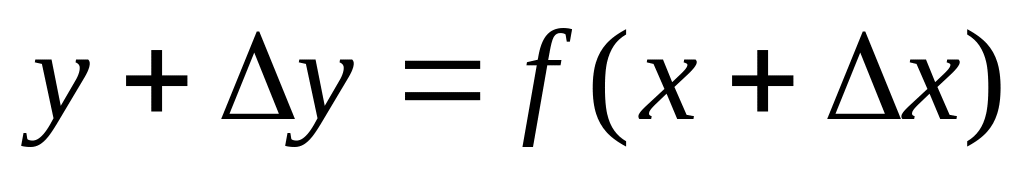2. найти ;

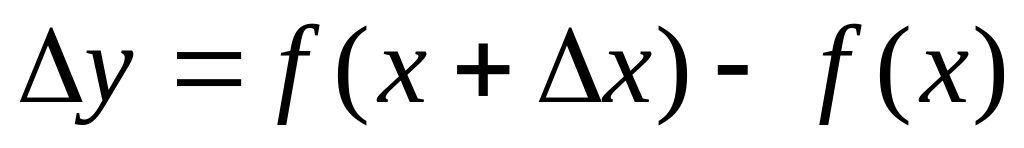3. составить отношение ;

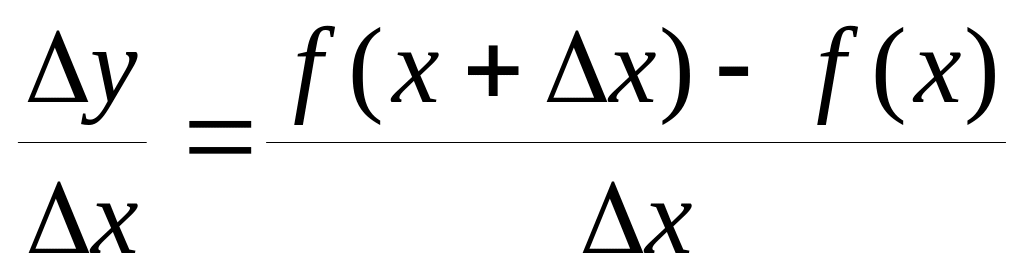4. найти предел этого отношения при т.е.

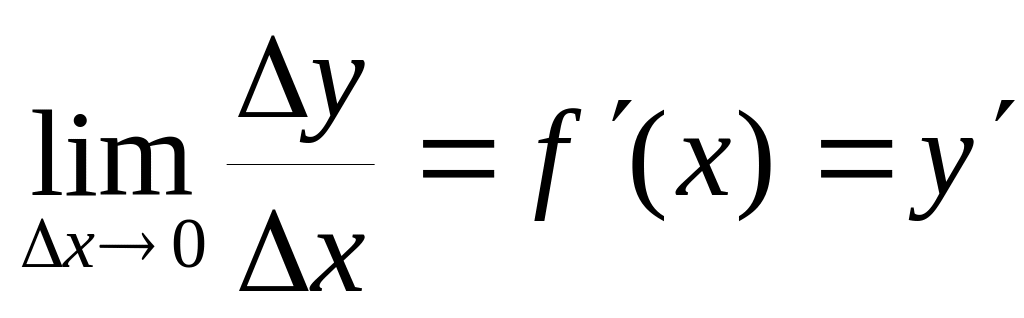
Пример 5.1. Дана функция . Найти . Воспользуемся четырехшаговой схемой.

1) .

2) .

3) .

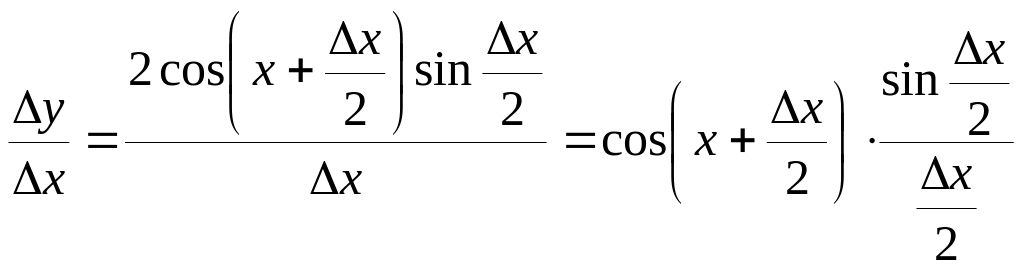4) 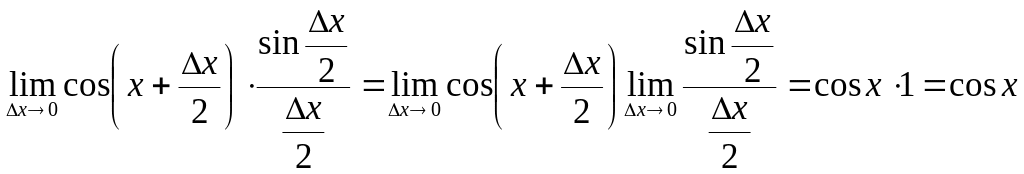, здесь один из пределов равен 1 как первый замечательный предел (§ 4.8).

Итак, получили производную синуса

.

5.6. Таблица производных основных элементарных функций

Пользуясь четырехшаговой схемой и свойствами основных элементарных функций можно получить производные этих функций, которые приведены в следующей таблице:

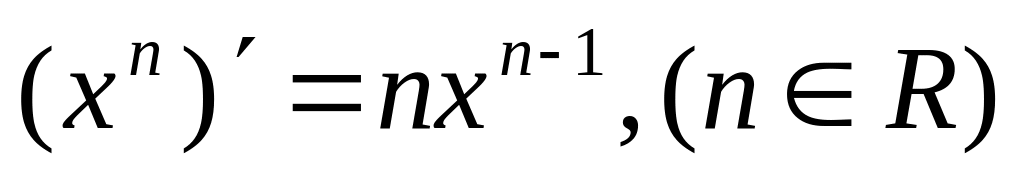
1)	8)
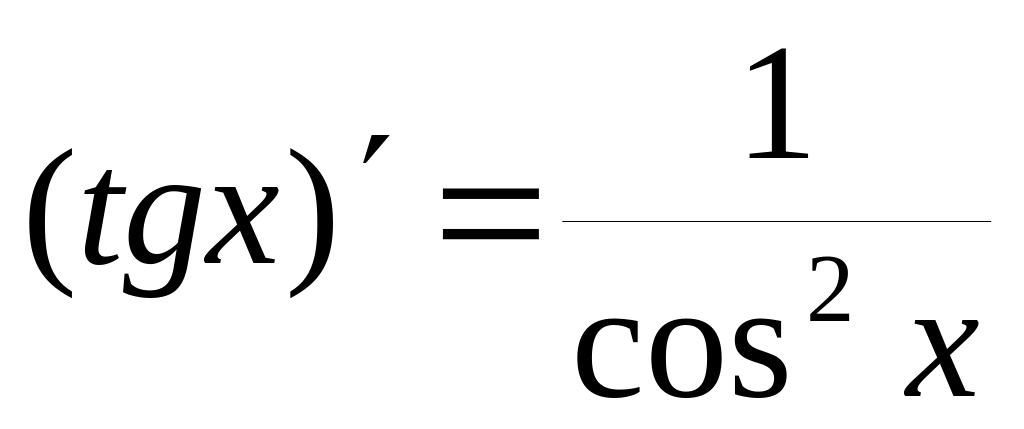
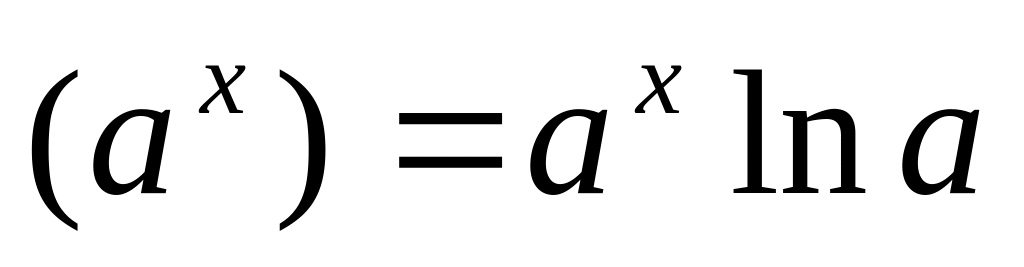
2)	9)
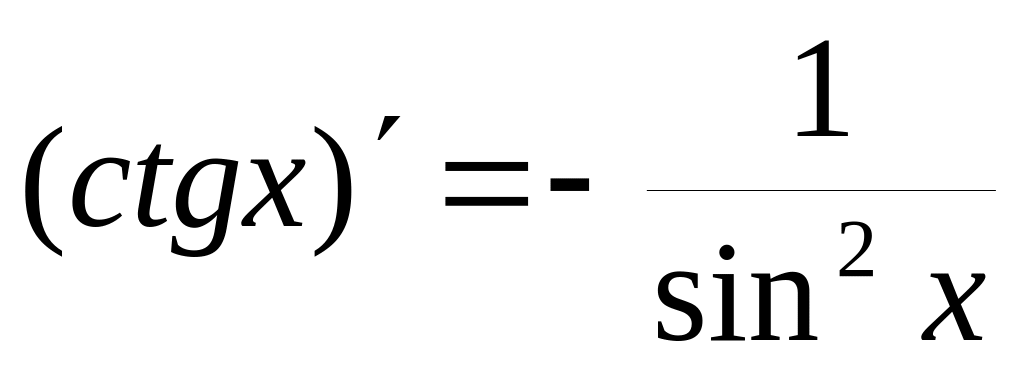
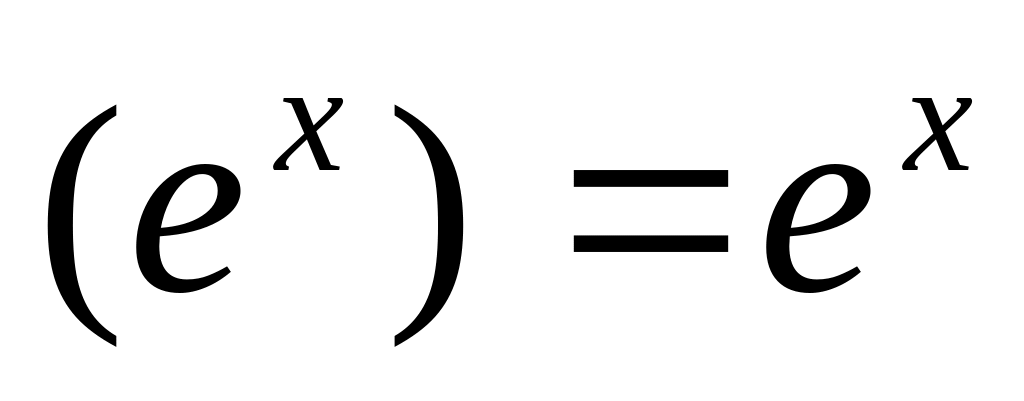
3)	10)
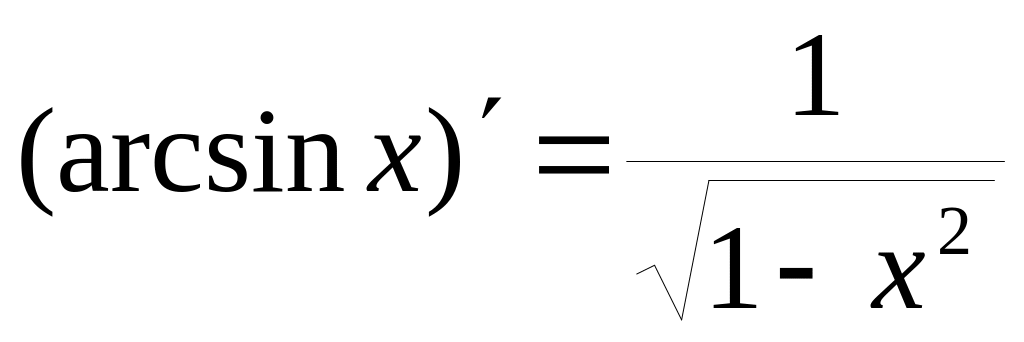
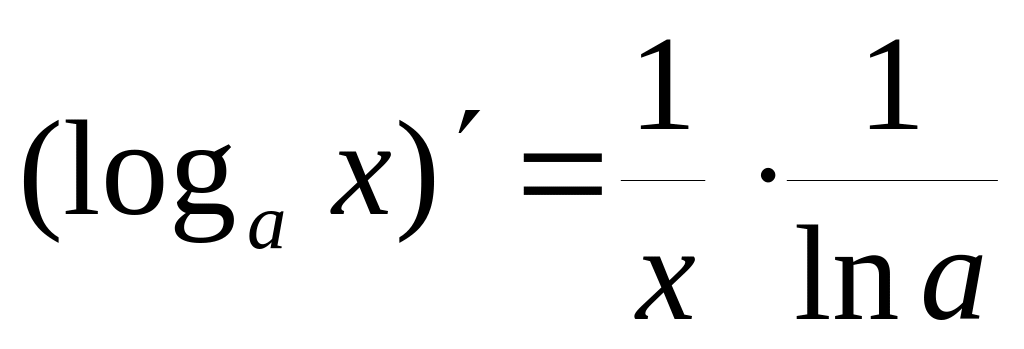
4)	11)
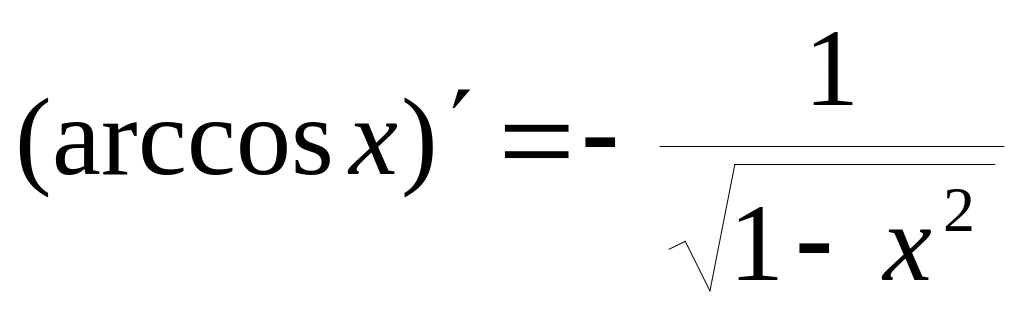
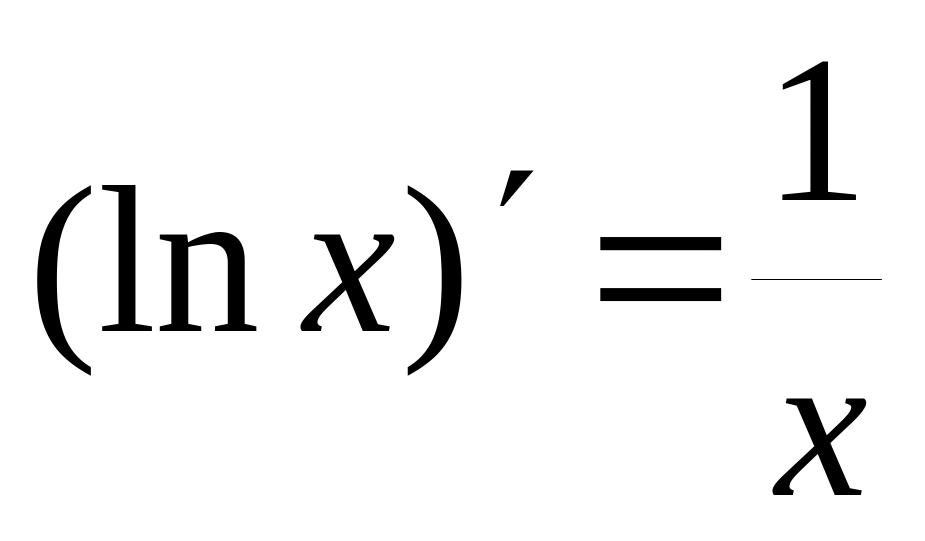
5)	12)
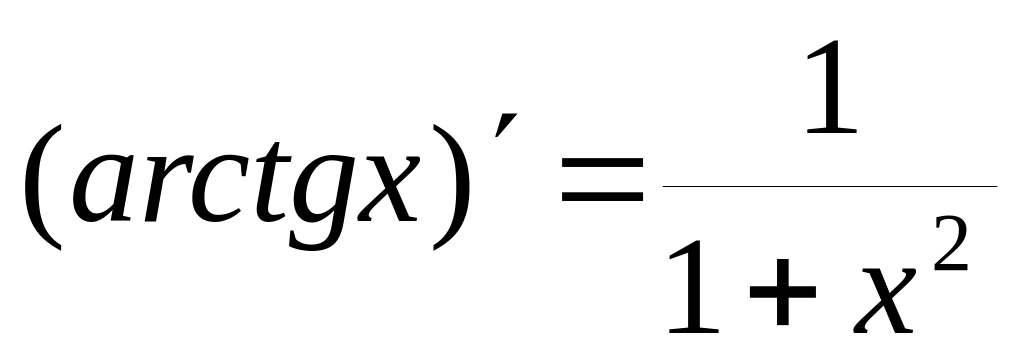
6)	13)
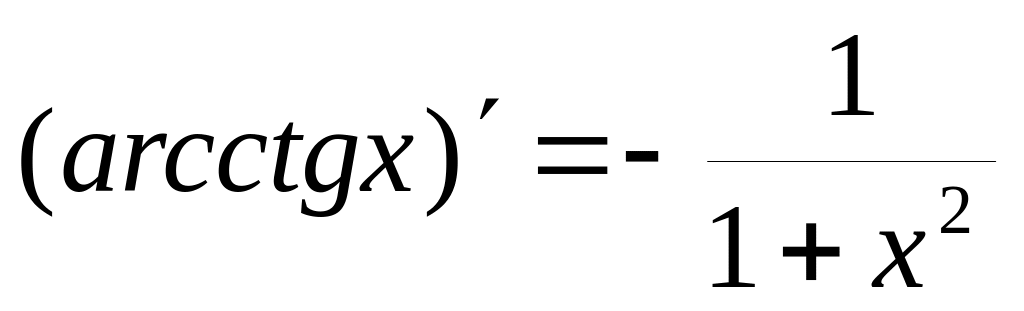
7)

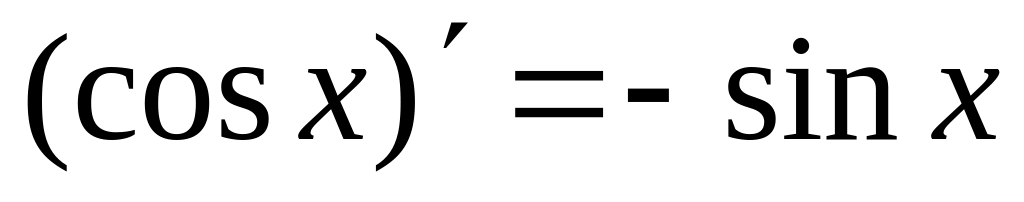
Здесь неуместно рассматривать вывод каждой из формул. Их вывод можно найти в полных учебниках математического анализа.

Для успешного овладения техникой дифференцирования необходимо формулы 1) – 13) запомнить.