1.3. Действия над матрицами. Обратная матрица. Ранг матрицы

Для матриц вводится понятие равенства и операции умножения на число, сложения матриц, умножения матриц. Рассмотрим их по порядку.

Две матрицы А = и В = называются равными, если они имеют одинаковый размер если равны все их соответствующие элементы, то есть = , для всех i, k.

К линейным операциям над матрицами относятся умножение матрицы на число и сложение матриц.

Умножение на число. Произведением матрицы А = на число  называется матрица того же размера, все элементы которой равны соответствующим элементам матрицы А, умноженным на , то есть

А=А= (1.4)

Пример 1.6.

При умножении матрицы на число 0 получим нуль-матрицу.

Сложение матриц. Суммой двух матриц А = и В = , имеющих одинаковый размер, называется матрица С, элементы которой равны суммам соответствующих элементов слагаемых матриц, то есть

С=А+В= + = (1.5)

Пример 1.7.

В частности очевидно, что А + В = В + А, А+ О = А.

Матрицу (-1) А = = -А называют противоположной матрице А. Тогда А - А = О, то есть сумма противоположных матриц равна нуль-матрице. Вычитание двух матриц можно рассматривать как сложение с противоположной матрицей : А+(-В) = А – В=  = .

Пример 1.8.

Линейные операции над матрицами обладают основными свойствами действий над числами. Над матрицами можно выполнять действия, комбинируя умножение на число, сложение, вычитание.

Умножение матрицы на матрицу,

Пусть даны две матрицы А = и В = , размеры которых связаны следующим условием: число столбцов матрицы А равно числу строк матрицы В - такие матрицы называют согласованными. Произведением двух согласованных матриц А и В называется матрица С = , элементы с_ik которой равны сумме попарных произведений элементов i-й строки матрицы А на соответствующие элементы k-гo столбца матрицы В:

c_ik = a_i1b_1k + a_i2b_2k +…+ a_inb_nk (1.6)

Матрица С = АВ имеет число строк такое же как у матрицы А, а число столбцов такое же, как у матрицы В, то есть ее размер :

С =

Для квадратных матриц n-го порядка умножение всегда возможно.

Пример 1.9. Найти произведение двух согласованных матриц

При умножении матриц закон переместительности не выполняется, то есть АВ  ВА.

Только при умножении квадратной матрицы на единичную или нулевую матрицы того же порядка справедливы равенства АЕ = ЕА = А и АО = ОА = О.

Для квадратных матриц определено возведение матрицы в целую положительную степень: .

Еще одна операция – транспонирование матрицы. Матрице А ставится в соответствие матрица , получаемая из матрицы А при замене строк столбцами, а столбцов строками, например:

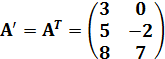
Порядок (нумерация) строк и столбцов сохраняется, а размеры матрицы изменяются с на .

Операция транспонирования используется, в частности, для вычисления обратной матрицы. Понятие это определяется только для квадратных невырожденных (неособых) матриц, определители которых отличны от нуля, т.е.

(1.7)

Матрица обратная матрице А определится соотношением

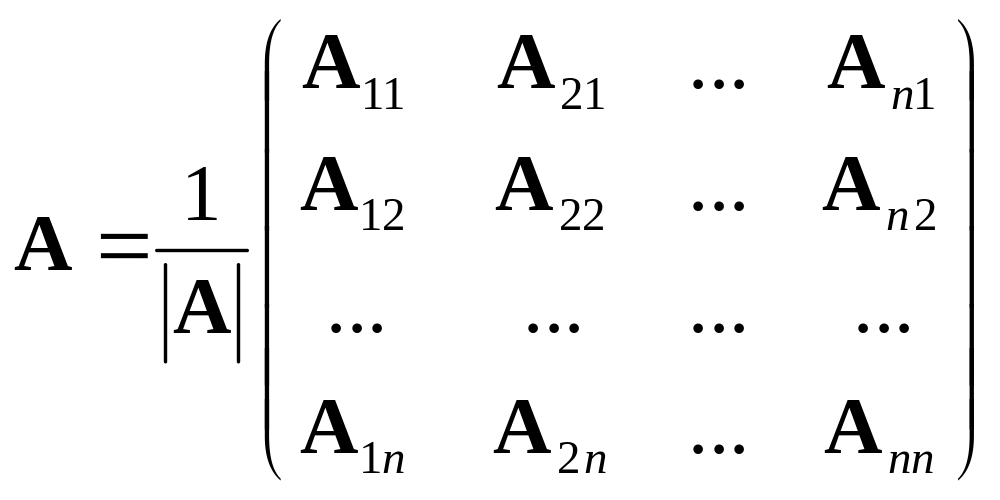(1.8)

т.е. обратная матрица равна произведению транспонированной матрицы алгебраических дополнений матрицы А на число, обратное определителю матрицы А.

Матрицы связаны соотношением

(1.9)

Группу операций, включающую в себя:

1. Исключение нулевой строки (столбца);

2. Умножение всех элементов строки (столбца) на отличное от нуля число;

3. Перемена местами строк (столбцов);

4. Прибавление к элементам строки (столбца) соответственных (стоящих на тех же местах) элементов другой строки (столбца) умноженных на одно и тоже число.

5. Транспонирование;

называют элементарными преобразованиями матрицы и говорят, что они приводят к появлению эквивалентной матрицы.

 символ эквивалентности.

Операции эти используются, в частности, для отыскания важной характеристики называемой рангом матрицы и обозначаемой символом .

Рангом матрицы А называют наивысший порядок отличного от нуля минора этой матрицы. Показано, что ранг матрицы равен числу ее строк, не обнуляемых элементарными преобразованиями. Это позволяет предложить «экономный» способ отыскания ранга матрицы.

Пример 1.10 Найти ранг матрицы

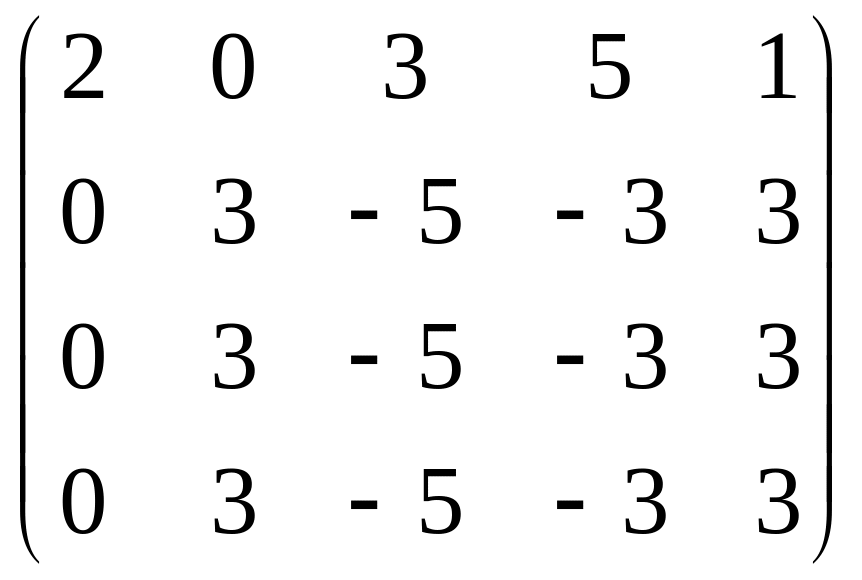
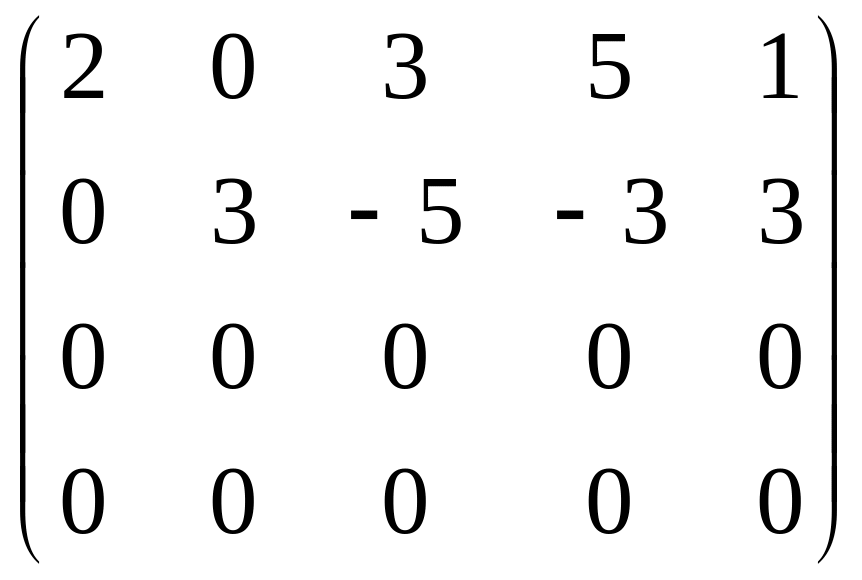
Осуществляем цепочку элементарных преобразований, приводящих матрицу к виду степенчатой. (1) – умножим первую строку на -2 и прибавим ко второй, (2) – умножим первую строку на -1 и прибавим к четвертой. В новой матрице, эквивалентной исходной, три одиноковых строки. (3) – умножим вторую строку на -1 и прибавим к третьей, (4) – умножим вторую строку на -1 и прибавим к четвертой. В новой матрице две нулевых строки. (5) – исключаем нулевые строки. Число строк, необнуленных элементарными преобразованиями равно 2 и .