2.4. Разложение вектора по осям координат

П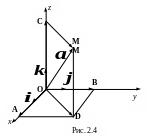 усть свободный вектор, начало которого совпадает с началом прямоугольной системы координат (рис.2.4) Спроектируем точку М на плоскость хОу. Получим точку D, которую спроектируем на оси Ох и Оу в точки А и В. Пусть точка С - проекция точки М на ось Оz. Построим векторы , , , a также единичные векторы (орты), имеющие общее начало в точке О.

По правилам сложения векторов получим

= + = + +

Любой вектор можно представить как произведение его модуля на единичный вектор его направления

Следовательно, = , = , = , где Х, Y, Z - проекции вектора на оси координат. Таким образом,

, (2.4)

где слагаемые, стоящие в правой част формулы называются компонентами (составляющими) вектора . Короче можно записать вектор так:

, (2.5)

где проекции вектора на оси координат называют координатами вектора. В дальнейшем мы часто будем переходить от записи вектора в компонентах к записи в координатах и обратно. Равные векторы имеют равные соответствующие координаты.

Если начало вектора не совпадает с началом координат и , где М₁(х₁, у₁, z₁), M₂(x₂, y₂, z₂) то проекции такого вектора на оси будут равны X=x₂ – x₁, Y=y₂ – y₁, Z=z₂ – z₁. И тогда запись вектора в координатной форме

(2.6)

2.5. Линейные операции над векторами, заданными в координатной форме

Умножение вектора на число.

Пусть дан вектор и число . Найдем  . Умножим число , на вектор , представленный в компонентах:

(2.7)

Итак, чтобы умножить число на вектор (или вектор на число) надо умножить каждую координату вектора на это число. Условие коллинеарности в координатной форме запишется так = = , а это равенство возможно, если . Таким образом , т.е. пропорциональность координат – необходимое и достаточное условие коллинеарности векторов.

Сложение векторов.

Пусть даны два вектора и . Найти . Складывая векторы, запишем их в компонентах. Получим

Итак, складывая два вектора, получим новый вектор, координаты которого равны сумме соответствующих координат слагаемых векторов. Формулу (2.7) можно распространять на любое конечное число слагаемых.

2.6. Скалярное произведение двух векторов

Скалярным произведением двух данных векторов и называется произведение модулей этих векторов на косинус угла между ними:

, где . (2.9)

Свойства скалярного произведения:

1) = , то есть выполняется закон переместительности;

2) , выполняется закон распределительности;

3) , выполняется закон сочетательности с числовым множителем;

4) , если .

Итак, условие перпендикулярности двух векторов:

если и , то (2.10)

Из формулы (2.9) получаем формулу для выражения угла между двумя векторами

(2.11)

В частности, или , то есть скалярный квадрат равен квадрату модуля.

2.7. скалярное произведение векторов, заданных в координатах

пусть даны два вектора в координатах , . Умножим их, записав в компонентах и используя свойства скалярного произведения

где , , , так как - взаимно перпендикулярны;

, , как скалярные квадраты единичных векторов.

Таким образом, , (2.12)

Если , то скалярный квадрат , но , как было показано выше, следовательно, , откуда

, (2.13)

а если вектор задан координатами начальной М₁ и конечной М₂ точек, как в формуле (2.6), то его модуль

(2.14)

Очевидно, что формулу (2.11) можно записать, используя (2.12) и (2.13) в виде

(2.15)

Эта формула позволяет вычислять угол между векторами, заданными в координатах.

Пример 2.1. Найти угол между векторами , .

Решение. По формуле (2.15) получим

Все, что было сказано о геометрических векторах в пространстве трех измерений, распространяется на векторы, заданные на плоскости, то есть двухмерные.