4.7. Сравнение бесконечно малых

Пусть несколько бесконечно малых , , , … являются функциями одного и того же аргумента x и стремятся к нулю при или . Будем рассматривать их отношения, пользуясь следующими определениями:

1. Если , то  и  называются бесконечно малыми одного порядка.

2. Если , (а ), то  называется бесконечно малой высшего порядка по сравнению с , а  - бесконечно малой низшего порядка, по сравнению с .

3. Если , то  и  - эквивалентные бесконечно малые, т.е.:   .

4.8. Два замечательных предела

1) Предел функции при .

Ф ункция не определена при x = 0, так как числитель и знаменатель дроби обращается в нуль. Такое выражение называют неопределенностью вида . Найдем предел этой функции при . Рассмотрим окружность радиуса 1 (рис. 4.2). Обозначим центральный угол МОА через x, где . Непосредственно из рисунка 4.2 видно, что площадь сектора МОА заключена между площадями треугольников МОА и СОА:

пл. МОА < пл. сект. МОА < пл. СОА

или , или после сокращения на , .

Разделив почленно на , получим или . Переходя к пределу при и учитывая, что , и , видим, что переменная заключена между величинами, имеющими один и тот же предел 1. Тогда, на основании теоремы 5 о действиях с пределами имеем

(4.1)

Отсюда следует, что sin x  x (sin x эквивалентен х) при .

2. Число е. Натуральные логарифмы. Экспонента.

Теорема. Функция стремится к числу е при , то есть

, (4.2)

где число е  2,718281828… Во многих случаях достаточным является приближение е  2,72. Это число прочно вошло в математику и широко используется.

Логарифмы с основанием е называют натуральными логарифмами и обозначают символом ln. Если , то

(4.3)

Связь между десятичными и натуральными логарифмами выражается следующей формулой перехода

(4.4)

где число называется модулем перехода.

Еще одним приложением числа е является показательная функция с основанием е – экспонента:

(4.5)

Функции и табулированы, то есть существуют их таблицы.

4.9. Непрерывность функции

4.9.1. Приращение аргумента и приращение функции

П усть функция определена в точке х = х₀ и некоторой ее окрестности с центром в точке х₀. Пусть . Если х получит некоторое (положительное или отрицательное) приращение х и станет равен , то и функция у получит некоторое приращение у. Новое приращенное значение функции будет (рис. 4.5). Итак, разность - приращение аргумента; разность - приращение функции.

4.9.2. Непрерывность функции в точке

Функция называется непрерывной в точке х₀, если она определена в этой точке и некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то есть

(4.6)

Пример 4.3. Докажем, что функция непрерывна в любой точке х₀. Имеем . Тогда . Пользуясь условием (4.6), найдем предел . Это и доказывает непрерывность функции.

Можно доказать, что всякая элементарная функция непрерывна в той точке, в которой она определена. Условие непрерывности (4.6) можно записать и так , где - постоянная величина, откуда . Приращение , если и тогда . Таким образом получим . Но , следовательно, . Иначе говоря, для того, чтобы найти предел непрерывной функции при , достаточно в выражение функции подставить , что мы уже делали в примерах 4.1 и 4.2.

Пример 4.4. Функция непрерывна в любой точке и потому .

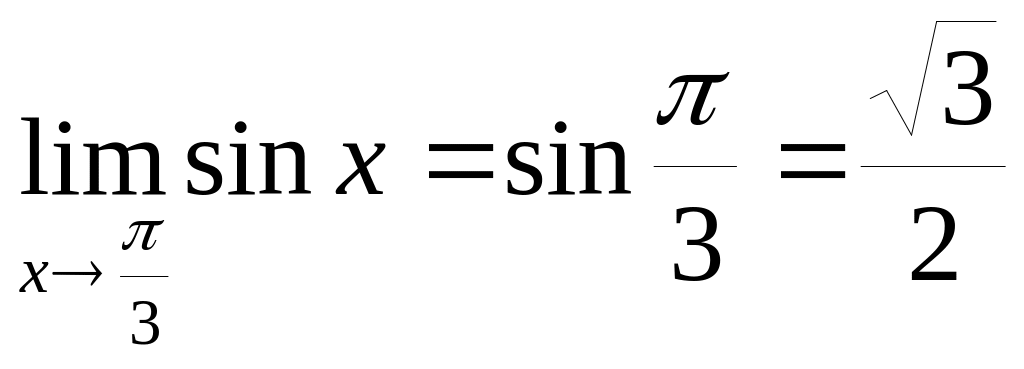Если функция определена в точке и ее окрестности и если , то она непрерывна в точке .

Если функция непрерывна в каждой точке некоторого интервала (а, b) и непрерывна на концах этого интервала справа и слева, то она называется непрерывной на отрезке [а, b].

Разрывы функций делят на разрывы первого и второго ряда. Если , , а не существует – то в точке испытывает разрыв первого рода типа скачок.

Пример: в точке .

Если ,а в - не существует, то функция в точке испытывает устранимый разрыв первого рода.

Пример: в точке .

Разрыв, не являющийся не являющийся разрывом первого рода, называют разрывом второго рода.

Примеры:

при , (1)

или

при . (2)

Такие разрывы как (2) ( ) называют бесконечными.