11.7. Дифференциальный оператор Гамильтона (оператор набла)

Под оператором набла понимают сумму частных производных по трем координатным осям. В декартовой системе координат он запишется так:

.

Формально его можно рассматривать как вектор. Оператор набла может быть применен к скалярным и векторным функциям. Та функция, действие над которой хотят произвести (дифференцирование ее по координатам или, другими словами, «пространственное» дифференцирование), пишется справа от оператора набла. Если же справа от него не указана эта функция, то сам по себе оператор набла не употребляется. Здесь можно провести аналогию с хорошо известными понятиями каких-либо других функций. Так, например, если написано sin , то совершенно ясно, что речь идет о синусе угла , т. е. о совершении определенной операции (нахождении синуса) угла . Если же было бы написано sin и после значка sin угол отсутствовал, то такая запись была бы лишена смысла.

Применим оператор  к потенциалу . С этой целью запишем

.

Если сравнить последнее выражение с (11.8), то можно заметить, что правые части у них одинаковы. Следовательно, равны и левые. Поэтому

grad=.

Другими словами, запись  эквивалентна записи qrad , а «приписывание» слева к какой-либо скалярной функции (в нашем случае к ) оператора  означает взятие градиента от этой скалярной функции.

11.8. Выражение градиента потенциала в цилиндрической и сферической системах координат

В цилиндрической системе (обозначения см. на рис. 11.4,а):

. (11.10)

В сферической системе (обозначения см. на рис. 11.4, б):

. (11.11)

Р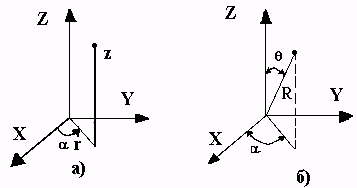 ис. 11.4. Цилиндрическая (а), сферическая (б) системы координат.

11.9. Поток вектора через элемент поверхности и поток вектора через поверхность

Пусть в векторном поле (например, в поле вектора напряженности электрического поля Е) есть некоторый элемент поверхности, площадь его с одной стороны численно равна ds. Выберем положительное направление нормали (перпендикуляра) к элементу поверхности. Вектор ds в некотором масштабе на рис.11.5 равен площади элемента поверхности, а его направление совпадает с положительным направлением нормали. Будем считать, что площадь элемента достаточно мала, чтобы в пределах этого элемента вектор Е можно было считать одним и тем же во всех точках. Если бы Е было перпендикулярно ds, то вектор Е не пронизывал бы элемент поверхности; если E будет направлено по ds , то через данный элемент поверхности будет максимальный поток вектора Е. В общем случае поток вектора Е через элемент поверхности ds определится скалярным произведением Eds.

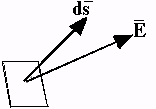
Рис. 11.5. Поток вектора через элемент поверхности d .

Произведение Еds является величиной скалярной. Следовательно, поток вектора через элемент поверхности есть величина скалярная. Поток вектора может оказаться положительным или отрицательным. Если скалярное произведение Еds окажется положительным, то это будет означать, что поток вектора направлен в сторону ds. Отрицательное значение потока вектора означает, что он направлен в обратную сторону. Если поверхность, через которую ищется поток вектора, велика, то тогда уже нельзя считать, что во всех точках ее Е одна и та же. В этом случае поверхность подразделяется на отдельные элементы малых размеров, и полный поток вектора через поверхность будет равняться алгебраической сумме потоков через все элементы поверхности. Сумма потоков может быть записана в виде интеграла .

Значок s под знаком интеграла означает, что суммирование производится по элементам поверхности. Если поверхность, через которую ищется поток вектора, замкнутая, то это обстоятельство находит свое выражение в том, что на знаке интеграла ставится кружок:

.