ПояснениЯ к решению задач

Для успешного прохождения этого раздела необходимо вспомнить сущность известных из главы 11 понятий, как, например, электрическое поле, напряженность поля, заряд, потенциал, смещение и тд.

Основу расчёта потенциальных полей составляет теорема Гаусса в интегральной и дифференциальной формах. В интегральной форме эта теорема записывается так:

,

где , ε΄ε₀ - диэлектрическая проницаемость среды, умножнная на диэлектрическую проницаемость вакуума; Е- вектор напряжённости электрического поля; dS-вектор элементарной площадки; Q- заряд, охватываемый поверхностью интегрирования S.

Та же теорема в дифференциальной форме, записанная через потенциал, часто называется уравнением Пуассона

или уравнением Лапласа

где: φ- потенциал поля; ρ- объёмная плотность заряда; - дифференциальный оператор, имеющий в прямоугольных координатах выражение

Первая запись соответствует случаю, когда в рассматриваемой точке поля имеется объёмный заряд с плотностью ρ, вторая запись соответствует случаю, когда в данной точке никаких зарядов нет. Решение, дающее потенциал электрического поля, будет единственно правильно, если оно:

1. удовлетворяет уравнению Лапласа во всём пространстве, лишенном зарядов,

2. удовлетворяет граничным условиям.

Существенным элементом расчёта поля является определение постоянных, получающихся при интегрировании уравнения Лапласа. Эти постоянные находятся из граничных условий.

Под граничными условиями в электростатическом поле понимается следующее:

1. Поверхности проводников должны быть эквипотенциальными;

2. Интегралы от вектора смещения по поверхностям проводников равны их суммарным зарядам;

Если имеем неоднородный диэлектрик, то должны быть соблюдены условия на границе раздела диэлектриков.

а) Е_1t=E_2t или ,

где t перемещение вдоль пути, лежащего на поверхности раздела диэлектриков;

б) D_1n=D_2n или ε΄₁ε_{0 ,}

где, n перемещение в направлении, перпендикулярном к поверхности раздела;

в) φ₁=φ₂ на границе, так как потенциал непрерывен. Из указанного выше условия единственности решения вытекают важные следствия, которые являются исчерпывающим обоснованием метода зеркальных изображений.

Следствие 1. Поле между двумя эквипотенциальными поверхностями не изменится, если рассматривать эти поверхности, как поверхности проводников, которыми сообщены соответствующие потенциалы.

Следствие 2. Поле внутри некоторой области не изменится, если истинное распределение зарядов вне этой области заменить фиктивным распределением, но обеспечивающим прежние граничные условия.

Примеры РешениЯ задач

Задача 1. Точечный заряд q находится на расстоянии d от бесконечного проводника, занимающего левое полупространство. Определить поле в правом полупространстве и плотность зарядов, индуцированных зарядом q на поверхности проводника.

Р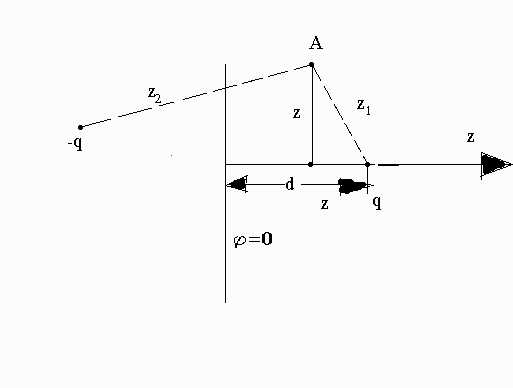 ешение. Рассмотрим поле совокупности двух зарядов: заданного заряда q и его зеркального изображения -q. Поле совокупности этих зарядов удовлетворяет граничным условиям задачи, из чего на основании теоремы единственности следует, что поле это тождественно с искомым полем заряда q и зарядов индуцированных им на поверхности бесконечного проводника.

Рис.1.

Введём цилиндрическую систему координат, ось которой направлена вправо и проходит через заряд q , а плоскость z=0 совпадает с поверхностью проводника. Расстояние произвольной точки А от зарядов ⁺q и ^--q равно соответственно

; .

Потенциал в точке А:

;

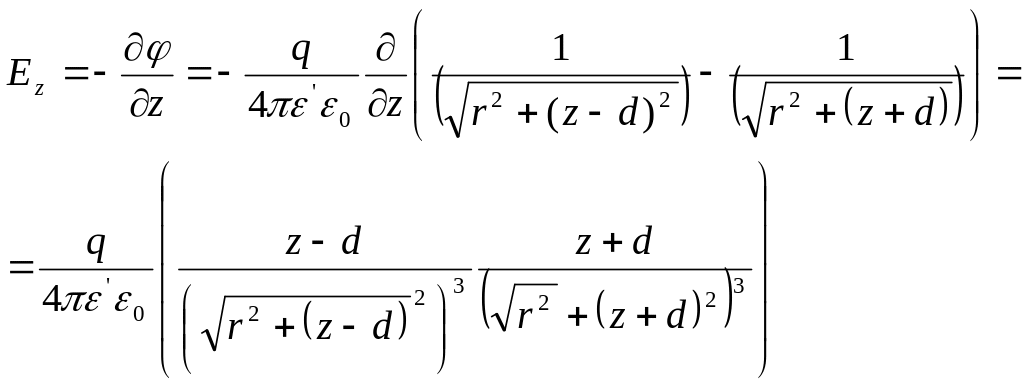
На поверхности проводника (z=0).

где R - расстояние элемента поверхности проводника от заряда q.

Плотность заряда

.

Задача 2. В цилиндрическом конденсаторе с воздушной изоляцией вокруг внутреннего электрода располагается объёмный заряд (короны) с объёмной плотностью ρ. Толщина слоя объёмного заряда задана (рис. 2). Плотность заряда на поверхности внутреннего провода равна σ. Внешний электрод заземлён (φ=0). Найти закон изменения напряжённости электрического поля в зависимости от расстояния от оси.

Решение. Решим задачу, применяя теорему Гаусса, в интегральной форме

.

При r r₀ напряжённость поля равна нулю.

При r₀ r r₁ имеем

где S₁=2πr₀ - поверхность внутреннего цилиндра единичной длины.

r2

r1

Рис.2

,

так как в силу круговой симметрии поля вектор направлен по нормали к поверхности интегрирования

.

При r₁ r r₂

_.

Задача 3. Пример на расчёт потенциальных полей. В цилиндрическом очень длинном конденсаторе потенциал внутренней обкладки равен нулю. Потенциал наружной обкладки равен φ₂. Требуется найти распределение потенциала между обкладками. Диэлектрик - воздух. Геометрические размеры обкладки даются на рис. 3.

r1

r2

Рис.3

Решение:

Будем исходить из уравнения Лапласа. Наличие цилиндрической симметрии делает естественным записать эти уравнения в цилиндрических координатах

. (1)

Соображения симметрии, а также то, что цилиндр длинный, позволяют заключить, что значение потенциала φ зависит лишь от r (расстояния от общей оси цилиндров) и не зависит ни от θ ни от z.

Таким образом, уравнение (1) превращается в

.

Решение этого уравнения

φ=Аlnr + B. (2)

где А и В произвольные постоянные. Для их определения воспользуемся граничными условиями: При r = r₁ φ=0

При r = r₂ φ = φ₂

и значит

. (3)

Совместное решение системы (3) даёт:

, .

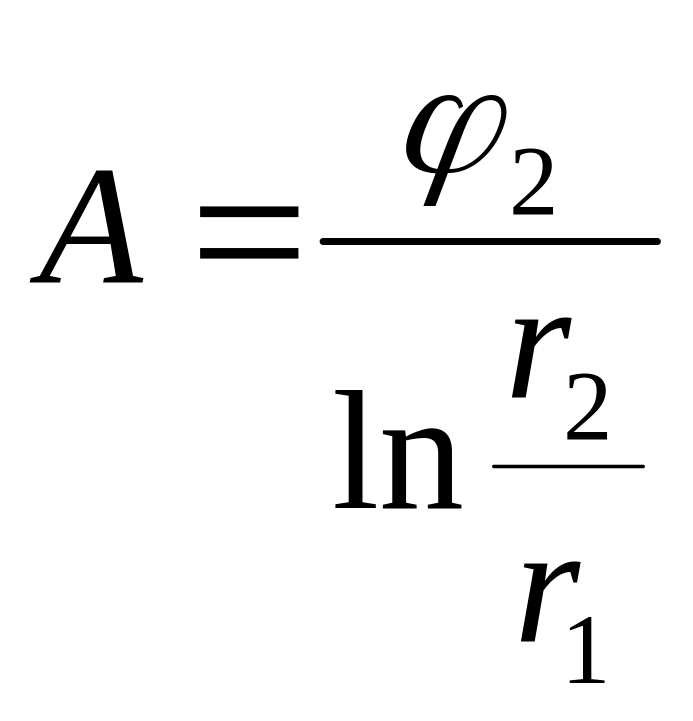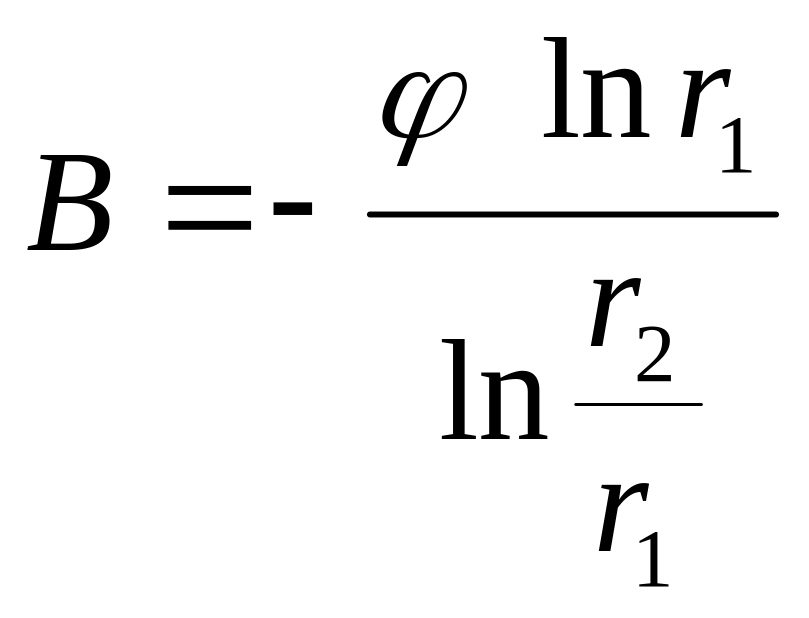Окончательное решение, соответствующее заданному очертанию электродов, получим, вставив найденное значение постоянных в (2):

.
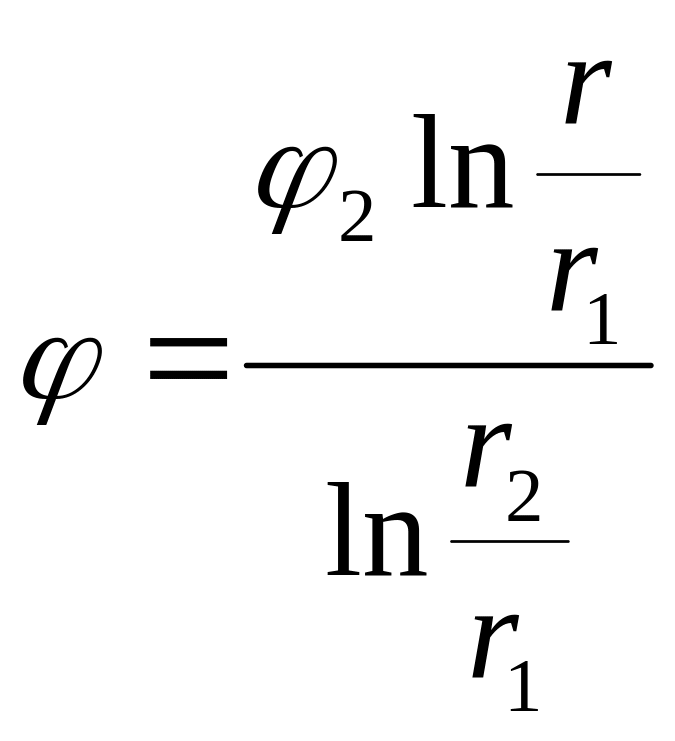